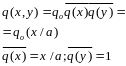- •Саратовский государственный технический университет расчет пологой оболочки
- •Саратов 2010 введение
- •Цель работы
- •Постановка задачи
- •Задание на работу
- •Определение величин изгибающих моментов Mx, My, мембранных усилий Nx, Ny, s и приведеных поперечных сил ,
- •Пример нахождения коэффициентов
- •Пример вычисления коэффициентов разложения функций и и построения эпюр силовых факторов
- •Расчет контурных диафрагм оболочки
- •Порядок выполнения работы
- •Содержание и оформление отчета по работе
- •Контрольные вопросы
- •Варианты заданий
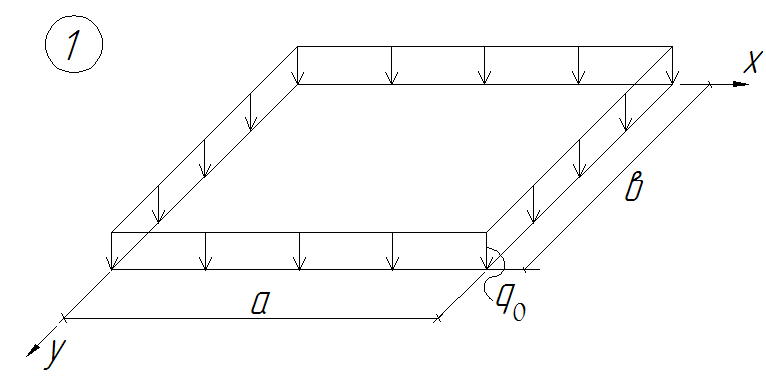
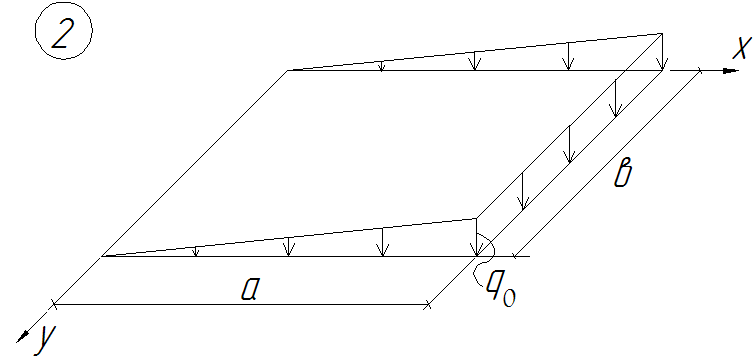
- •Схемы нагрузок
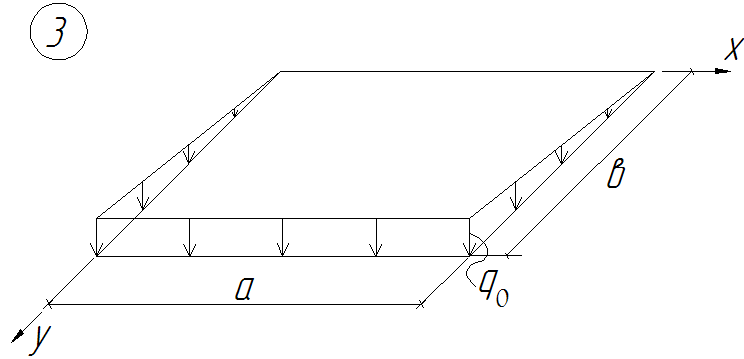
- •2) Схемы распределения нагрузки по плану оболочки
- •3) Геометрические размеры
- •Инструкция к программе «shell»
- •Программа «shell»
- •Контрольный пример
- •Содержание
- •Литература Основная
- •Дополнительная
Варианты заданий

Схемы нагрузок
24
2) Схемы распределения нагрузки по плану оболочки


3) Геометрические размеры
 =
20; 24; 30; 35; 40; 45; 50.
=
20; 24; 30; 35; 40; 45; 50.
Следующие размеры задаются преподавателем на всю группу:

25
Инструкция к программе «shell»
При выполнении расчетно-графической работы используется программа, составленная на языке Paskal 7.0 для ПЭВМ, в которых имеется данный алгоритмический язык [5]. Кроме того, возможен вариант использования файла программы SHELL.EXE, который может быть запущен практически на любой ПЭВМ. Программа предназначена для вычисления прогибов, изгибающих моментов, крутящего момента, поперечных сил, приведенных поперечных сил, мембранных нормальных и сдвигающего усилий для оболочек на прямоугольном плане, шарнирно опертых на диафрагмы.
Для работы с программой необходимо подготовить и ввести следующие исходные данные:
1)
A= (м) , B=b ( м) – размеры оболочки в плане по
осям x и y соответственно;
(м) , B=b ( м) – размеры оболочки в плане по
осям x и y соответственно;
2)
F1= (М), F2=
(М), F2= (М) – стрелы подъема контурных диафрагм
оболочки;
(М) – стрелы подъема контурных диафрагм
оболочки;
4) H=h (м) – толщину оболочки;
5)
PY=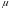 –
величину коэффициента Пуассона материала
оболочки;
–
величину коэффициента Пуассона материала
оболочки;
6)
 – матрицу коэффициентов ряда разложения
нагрузки, которая вводится построчно.
– матрицу коэффициентов ряда разложения
нагрузки, которая вводится построчно.
После
ввода исходной информации ПЭВМ выдает
на дисплей название работы “ Расчет
пологой оболочки”, исходные данные и
переходит к счету. В процессе счета ПЭВМ
выводит на дисплей построчно матрицы
коэффициентов
 и
и
 и для сечений
и для сечений
 значения
следующих функций
значения
следующих функций
 в
точках N = 1,2,…,9, соответствующих значениям
координаты x=0,
/8,
/4,
3
/8,
/2,
5
/8,
3
/4,
7
/8,
.
в
точках N = 1,2,…,9, соответствующих значениям
координаты x=0,
/8,
/4,
3
/8,
/2,
5
/8,
3
/4,
7
/8,
.
Далее
для сечений
 выводятся на дисплей значения следующих
функций
выводятся на дисплей значения следующих
функций
 в
точках N=1,2,…,9, соответствующих значениям
координаты y=0, b/8, b/4, 3b/8, b/2, 5b/8, 3b/4, 7b/8, b.
в
точках N=1,2,…,9, соответствующих значениям
координаты y=0, b/8, b/4, 3b/8, b/2, 5b/8, 3b/4, 7b/8, b.
Вычисления
по приводимой ниже программе проводятся
для значений
 =1
МПа, E= 40000 МПа.
=1
МПа, E= 40000 МПа.
В конце счета ПЭВМ печатает “Конец задачи “.
26
Программа «shell»
{$N+} program ProjectSHELL; uses WinCrt; Var WW,FF,Q: array [1..4,1..4] of extended;
W,MX,MY,HH,NX,NY,S,QX,QY,QXX,QYY,PI,PI2,PI3,PI4,PI8,KON,A,B,F1,F2,H,PY,KX,KY,E,D,IJAB,IJAB2,IJAB4,KXKY,KXKY2,X,Y: extended; I,J,K,L:integer;
begin Writeln(' RASCHET POLOGOY OBOLOCHKI ');
Write(' A= '); ReadLn(A); Write(' B= '); ReadLn(B); Write(' F1= '); ReadLn(F1);
Write('F2= '); ReadLn(F2); Write(' H= '); ReadLn(H); Write(' PY= '); ReadLn(PY);
E:=4E10; PI:=3.1415926535897932385;PI2:=PI*PI;PI3:=PI2*PI;PI4:=PI2*PI2;
PI8:=PI4*PI4; KX:=8*F1/(A*A+4*F1*F1); KY:=8*F2/(B*B+4*F2*F2); D:=E*H*H*H/(12*(1-PY*PY)); WRITELN('KX=',KX,' KY=',KY,' D=',D);
For I:=1 to 4 do begin For J:=1 to 4 do begin
WRITE(' Q[',I,',',J,']=');READLN(Q[I,J]); END;END;
For I:=1 to 4 do begin For J:=1 to 4 do begin
IJAB:=(I*I/A/A+J*J/B/B); IJAB2:=IJAB*IJAB; IJAB4:=IJAB2*IJAB2;
KXKY:=KX*J*J/B/B+KY*I*I/A/A; KXKY2:=KXKY*KXKY; KON:=D*PI8*IJAB4+E*H*PI4*KXKY2;
WW[I,J]:=Q[I,J]*PI4*IJAB2/KON; FF[I,J]:=Q[I,J]*E*H*PI2*KXKY/KON;
WRITELN(' WW[',I,',',J,']=',WW[i,j],' FF[',I,',',J,']=',FF[i,j]); END;END;
For L:=1 to 3 do begin Y:=B/2*(L-1); For K:=1 to 9 do begin X:=A/8*(K-1);
W:=0;MX:=0;NX:=0;NY:=0;HH:=0;S:=0;QX:=0;QXX:=0;
For I:=1 to 4 do begin For J:=1 to 4 do begin
W:=W+WW[I,J]*sin(I*PI*X/A)*SIN(J*PI*Y/B);
MX:=MX+WW[I,J]*D*(I*I/A/A+PY*J*J/B/B)*PI2*SIN(I*PI*X/A)*SIN(J*PI*Y/B);
HH:=HH-WW[I,J]*D*(1-PY)*I*J/A/B*PI2*COS(I*PI*X/A)*COS(J*PI*Y/B);
NX:=+NX-FF[I,J]*J*J/B/B*PI2*sin(I*PI*X/A)*SIN(J*PI*Y/B);
NY:=+NY-FF[I,J]*I*I/A/A*PI2*sin(I*PI*X/A)*SIN(J*PI*Y/B);
S:=+S-FF[I,J]*I*J/A/B*PI2*COS(I*PI*X/A)*COS(J*PI*Y/B);
QX:=QX+WW[I,J]*D*(I*I*I/A/A/A+I*J*J/A/B/B)*PI3*COS(I*PI*X/A)*SIN(J*PI*Y/B);
QXX:=QXX+WW[I,J]*D*(I*I*I/A/A/A+
(2-PY)*I*J*J/A/B/B)*PI3*COS(I*PI*X/A)*SIN(J*PI*Y/B); END;END;
WRITELN('X=',X,' Y=',Y); WRITELN('W=',W,' MX=',MX);
WRITELN('HH=',HH,' S=',S); WRITELN('NX=',NX,' NY=',NY);
WRITELN('QX=',QX,' QXX=',QXX); READLN;END;END;
For K:=1 to 3 do begin X:=A/2*(K-1); For L:=1 to 9 do begin Y:=B/8*(L-1);
W:=0;MY:=0;NX:=0;NY:=0;HH:=0;S:=0;QY:=0;QYY:=0;
For I:=1 to 4 do begin For J:=1 to 4 do begin
W:=W+WW[I,J]*sin(I*PI*X/A)*SIN(J*PI*Y/B);
MY:=MY+WW[I,J]*D*(PY*I*I/A/A+J*J/B/B)*PI2*SIN(I*PI*X/A)*SIN(J*PI*Y/B);
HH:=HH-WW[I,J]*D*(1-PY)*I*J/A/B*PI2*COS(I*PI*X/A)*COS(J*PI*Y/B);
NX:=+NX-FF[I,J]*J*J/B/B*PI2*sin(I*PI*X/A)*SIN(J*PI*Y/B);
NY:=+NY-FF[I,J]*I*I/A/A*PI2*sin(I*PI*X/A)*SIN(J*PI*Y/B);
S:=+S-FF[I,J]*I*J/A/B*PI2*COS(I*PI*X/A)*COS(J*PI*Y/B);
QY:=QY+WW[I,J]*D*(J*J*J/B/B/B+J*I*I/B/A/A)*PI3*SIN(I*PI*X/A)*COS(J*PI*Y/B);
QYY:=QYY+WW[I,J]*D*(J*J*J/B/B/B+
(2-PY)*J*I*I/B/A/A)*PI3*SIN(I*PI*X/A)*COS(J*PI*Y/B); END;END;
WRITELN('X=',X,' Y=',Y); WRITELN('W=',W,' MY=',MY);
WRITELN('HH=',HH,' S=',S); WRITELN('NX=',NX,' NY=',NY);
WRITELN('QY=',QY,' QYY=',QYY); readln;END;END;
WRITELN(' KONETCH ZADACHI '); READLN;END.
27