Определение величин изгибающих моментов Mx, My, мембранных усилий Nx, Ny, s и приведеных поперечных сил ,

Для определения в оболочке деформаций и напряжений необходимо построить эпюры прогиба и усилий моментной – рис.5 а и мембранной – рис.5 б групп.

а б

Рис. 5

8

Усилия и моменты в оболочке являются погонными, то есть приходящимися на единицу длины сечения оболочки и имеющими соответственно единицы измерения Н/М и Н М/М.

Необходимо обратить внимание на следующее: на контуре оболочки поперечную силу 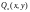или и крутящий момент можно заменить статически им эквивалентной приведенной поперечной силой или .

Для построения эпюр усилий и моментов необходимо подставить выражения (14) в формулы для усилий и моментов:

(15)

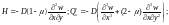
В результате этой подстановки получаем формулы:

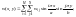(16)

9

Для каждой конкретной точки подставляем в формулы (16) значения и и находим интересующие нас значения функций.

Пример нахождения коэффициентов

При расчете оболочек необходимо вначале для заданной нагрузки определить коэффициенты в ряду разложения (7). Рассмотрим методику их определения на ряде примеров.

Пусть на оболочку действует распределенная нагрузка вида

В соответствии с вариантами заданий для имеем значения:

Представим коэффициенты разложения в виде:

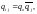(17)

где выражение для будет:

(18)

Все дальнейшие выкладки будем производить с точностью до . Вычислим входящие в (18) интегралы. Имеем:

(19)

Здесь использована замена переменных:

10

Интеграл в правой части равенства (19) , который в дальнейшем обозначаем через (i), равен:

(20)

Для значения , то есть для получаем:

(21)

Подставляя в это выражение конкретные значения i , получаем:

(22)

Для значения , то есть для получаем:

(23)

Аналогично вычисляется второй интеграл из выражения (18).

(24)

Здесь использована следующая замена переменных:

(25)

Обозначая интеграл в правой части равенства (24) через (j), получим:

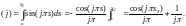(26)

(j=1, 2, 3, 4).

Для имеем:

(27)

11

Для получаем:

(28)

С учетом введенных обозначений выражение для имеет вид:

(29)

где величины (i) и (j) определяются согласно формулам (20 28).

Из полученных значений составляется матрица, в которой i задает номер строки, а j – номер столбца. Например, взяв для определенности значения , получим следующую матрицу коэффициентов :

(30)

Подставив значение , получаем матрицу коэффициентов , которая затем используется в дальнейших вычислениях.

Необходимо отметить, что величины коэффициентов (18) в разобранном выше примере вычислялись аналитически. Однако при практических расчетах оболочек покрытия для достижения точности по напряжениям необходимо удерживать в двойных рядах разложения функций прогиба и усилий (14) значительное число членов. При этом безусловно оптимальным является не аналитический, а численный подсчет величин коэффициентов (18) по формуле Симпсона [6], когда для вычисления величины необходимо использовать формулы:

При этом время вычисления определенного интеграла на ПЭВМ уменьшается в сотни раз, так как номера узлов в подынтегральной функ-

12

ции не проверяются на «чет» и «нечет» в самом цикле вычислений интеграла , в выражение которого входят коэффициенты целочисленного числового массива , включающие функцию . Напомним, что функция возвращает целую часть реального числа , равную в случае четности 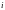и равную 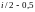в случае нечетности .

Отметим, что при используемой методике подсчета величины определенного интеграла становится возможным брать весьма малый шаг между узловыми значениями подынтегральной функции и тем самым существенно увеличить точность вычисления величины без ущерба для времени счета ПЭВМ.

Рассмотрим в качестве примера использования данной численной методики вычисление величины определенного интеграла вида

при различном числе участков деления интервала интегрирования «n».

Точное значение определенного интеграла а приближенные значения (с указанием числа отрезков n) равняются:

то есть скорость сходимости величины к точному значению весьма высока и для практических расчетов достаточно разбиения на n=64 участка.