
- •Саратовский государственный технический университет расчет балки-стенки
- •Содержание
- •Введение
- •Цель работы
- •Задание на работу
- •Теоретическая часть
- •Представление нагрузок с помощью рядов фурье
- •Расчет балки-стенки при помощи рядов фурье
- •Расчет балки-стенки по технической теории изгиба
- •Расчет балки-стенки с заданной точностью при действии нагрузок произвольного вида
- •Порядок выполнения работы
- •Контрольные вопросы
- •Варианты заданий
- •Литература
Порядок выполнения работы
I. Получить и при необходимости согласовать с преподавателем
задание.
2. Изучить теоретический материал, пользуясь руководством и реко-
мендованной литературой (1 час).
3. Провести разложение заданной нагрузки в одинарный тригонометри-
ческий ряд (1 час).
Изучить сходимость ряда разложения нагрузки до указанного преподавателем члена ряда (0,25 часа).
Для расчета на указанный преподавателем член ряда
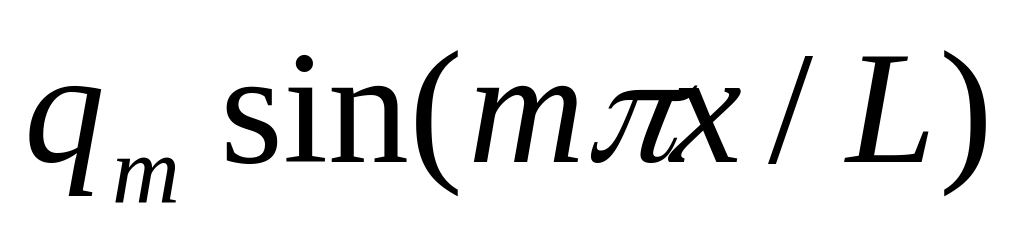 записать обыкновенное дифференциальное
уравнение, задавшись функцией
записать обыкновенное дифференциальное
уравнение, задавшись функцией
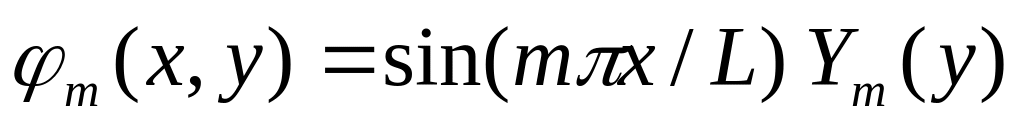 (0,25 часа).
(0,25 часа).
Найти коэффициенты функции
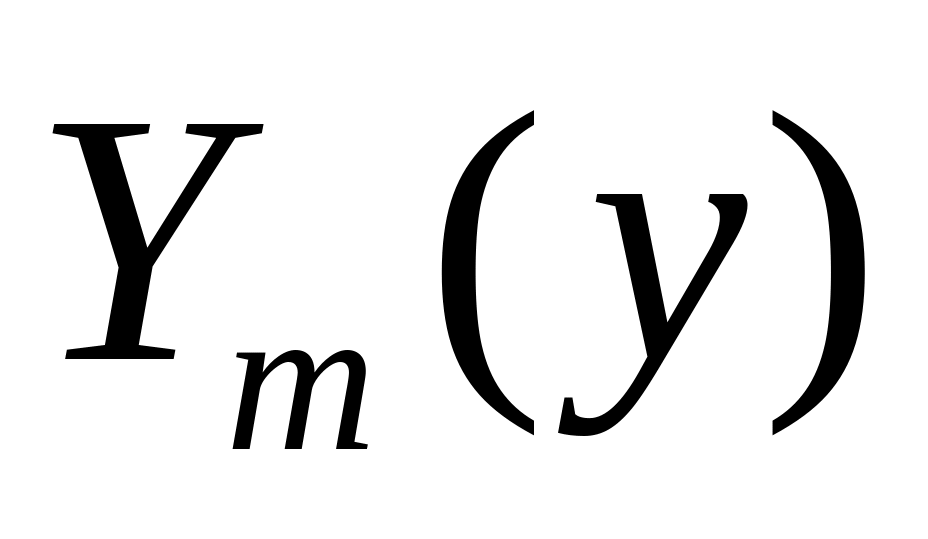 из краевых условий (1 час).
из краевых условий (1 час).Вычислить ординаты эпюр в заданных сечениях (1 час).
Решить задачу методами сопротивления материалов (0,5 часа).
Сопоставить точное и приближенное решение задачи и сделать соответствующие выводы (0,25 часа).
Расчетно-графическая работа выполняется в 5 семестре. На ее выполнение затрачивается примерно 5 часов из времени, отведенного на самостоятельную работу студента. Срок представления оформленной работы составляет три недели с момента выдачи задания.
СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА О РАБОТЕ
Отчет о работе должен выполняться в соответствии с приведенными примерами расчета и содержать следующие разделы:
вариант задания;
постановка задачи;
разложение заданной нагрузки в тригонометрические ряды с удержанием указанного числа слагаемых;
изучение скорости сходимости рядов разложения нагрузки;
запись обыкновенного дифференциального уравнения и граничных условий;
нахождение величин произвольных постоянных функции Y (у) из граничных условий на линиях ;
построение эпюр в заданных сечениях;
решение задачи методами сопротивления материалов;
сопоставление точного и приближенного решения задачи изгиба балки-стенки.
При оформлении работы на одной стороне листов формата А4 численные результаты иллюстрируются чертежами, выполненными в масштабе с использованием чертежных принадлежностей.
26
Контрольные вопросы
1. Какая задача называется плоской задачей теории упругости?
2. Чем различаются расчеты для плоского напряженного состояния
и плоской деформации?
3. Какие компоненты тензора напряжений определяют плоскую зада-
чу теории упругости?
4. Для чего вводится функция напряжений Эри?
5. Как записывается бигармоническое уравнение плоской задачи тео-
рии упругости?
6. Как формулируются краевые ycловия при расчете балки-стенки?
7. Дайте основные характеристики метода Фурье сведения двумерной
задачи теории упругости к одномерной.
8. Каким образом произвольные нагрузки раскладываются в тригоно-
метрические ряды Фурье?
9. Обоснуйте достаточность разложения действующих на балку-стенку
нагрузок в ряды Фурье или по синусам, или по косинусам.
10. Запишите формулы для коэффициентов рядов разложения: по сину-
сам, по косинусам, в полный ряд Фурье.
11. Каким способом получаются обыкновенные дифференциальные
уравнения
относительно функции
![]() ?
?
12. По каким формулам вычисляются напряжения в балке-
стенке?
13. Как находятся произвольные постоянные функции У(у) ?
14. Как разыскивается решение задачи изгиба балки при использовании
технической теории?
15. Каковы допустимые границы применения технической теории изгиба
балок?
16. Укажите способ получения решения задачи изгиба балки-стенки с
заданной степенью точности.
17. Укажите известные Вам способы упрощения расчетов балок-
стенок.
18. Каким образом исходные нагрузки можно представить в виде сим-
метричных и антисимметричных составляющих?
19. Элементами каких инженерных сооружений являются балки-
стенки?
27
