1. Принцип сохранения массы. Материальный баланс.

Д ля обычных (нерелятивистских) систем сумма всех масс, вошедших и вышедших через контрольную поверхность, равна изменению массы системы, ограниченной данной контрольной поверхностью (рис. 1):

,

где – потоки массы, кг/(с·м²) (с_i – усредненные составляющие скоростей входящих и выходящих потоков, относительные к контрольной поверхности и нормальные к ней, м/с; – плотность вещества в потоках, кг/м³); f_i – площади сечений, через которые втекают и вытекают потоки массы, м²; Δm – изменение массы системы в единицу времени, кг/с (для стационарных режимов Δm=0; для установившихся режимов усредненное по времени значение Δm=0 либо Δm=const, например в процессах наполнения или опорожнения).

Если потоки массы неоднородны по составу (например, смеси), то при отсутствии химических реакций для n-го компонента

,

где y_in – концентрация n-го компонента в i-м потоке, кг/кг; Δm_n – изменение массы n-го компонента в системе, кг/с (для стационарных состояний Δm_n=0, для установившихся – Δm_n=0 или Δm_n=const).

2. Принцип сохранения энергии. Энергетический баланс.

Для любой системы алгебраическая сумма всех внешних воздействий, которыми система обменивается с окружающими телами через контрольную поверхность, равна изменению энергии системы (рис. 2):

.

П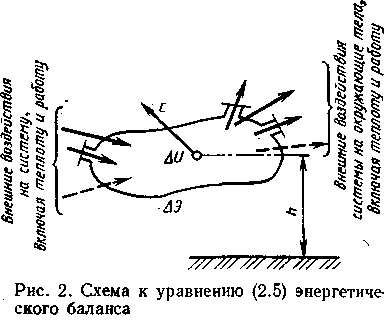 онятие «внешнее воздействие» употребляют в самом широком смысле: оно объединяет количества энергий всех видов, которыми система обменивается с окружающими телами.

При анализе криогенных систем в левой части уравнения сохранения энергии могут быть следующие величины:

L – механическая (электрическая) работа, Дж и Вт·ч (для процессов намагничивания – работа намагничивания); l – удельная работа, Дж/кг или Вт·ч/кг;

pv – работа гидродинамических сил каждой единицы массы на входе и выходе из контрольной системы, Дж/кг (р – давление, Па; v – удельный объем, м³/кг); работа гидродинамических сил на входе и выходе в общем случае пропорциональна удельному объему и нормальным напряжениям в потоке; если градиент скорости мал, то нормальная составляющая напряжений практически равна давлению р;

u – внутренняя тепловая энергия каждой единицы массы, пересекающей контрольную поверхность системы, Дж/кг;

е_к и е_п – кинетическая и потенциальная энергия каждой единицы массы, пересекающей контрольную поверхность, Дж/кг;

– энтальпия или удельная энергия потока (при малых скоростях) на входе или выходе из системы, Дж/кг;

– полная энтальпия, называемая также энтальпией адиабатически заторможенного потока (или удельная энергия потока при входе или выходе из системы), Дж/кг;

Q и q – теплота, передаваемая контрольной системе или теряемая ею под действием разности температур на контрольной поверхности или лучеиспускания, Дж и Дж/кг.

Величина ΔЭ в правой части уравнения представляет собой изменение энергии системы.

В общем случае для термомеханической системы:

закрытой

;

открытой (за время τ)

.

3. Теорема об изменении импульса.

При анализе силовых взаимодействий потоков криогенных жидкостей и газов, в частности с обтекаемыми профилями в лопаточных машинах, и расчете эжекторов широко используют теорему об изменении импульса (количества движения):

[Скорость изменения полного импульса системы]=

=[Равнодействующая всех внешних сил].

При отсутствии внешних сил полный импульс системы постоянен. Эта теорема является следствием 2-го закона Ньютона и в гидродинамической форме выражается уравнением Эйлера (рис. 4)

,

где m – масса системы, кг; С – скорость центра масс системы, м/с; F – результирующая внешних сил, Н.

Для стационарных и установившихся режимов при Δm=0

.

Поскольку c_i и С – векторы, то импульсы – тоже векторы. Сумма проекций скоростей изменения импульсов на любую из осей равна проекции результирующей внешней силы на эту ось. При стационарном вращательном движении алгебраическая сумма моментов импульсов секундных масс всех входящих и выходящих потоков относительно оси вращения равна моменту результирующей внешней силы относительно той же оси:

,

где r_i – кратчайшие расстояния от векторов с_i, до оси вращения, м; M_F – момент результирующей внешней силы F, Н·м. Произведение момента M_F и угловой скорости ω определяет мощность, Вт

.