
- •Раздел 6.
- •Раздел 6. Модели и алгоритмы решения задач численными методами с использованием математических пакетов Рекомендации по использованию учебного пособия
- •Тема 6.1. Элементы теории погрешностей
- •6.1.1. Точные и приближенные числа
- •6.1.2. Абсолютная и относительная погрешность
- •Тема 6.2. Методы решения нелинейных уравнений
- •6.2.1. Постановка задачи
- •Отделение корней (локализация корней);
- •Итерационное уточнение корней.
- •6.2.2. Отделение корней
- •6.2.2.1. Графическое отделение корней
- •6.2.2.2. Аналитическое отделение корней
- •6.2.3. Уточнение корней
- •6.2.3.1. Метод половинного деления
- •6.2.3.2. Метод итерации
- •6.2.3.3. Метод Ньютона (метод касательных)
- •6.2.3.4. Метод хорд
- •6.2.3.5. Сравнение методов решения нелинейных уравнений
- •6.2.4. Технология решения нелинейных уравнений средствами MathCad
- •Тема 6.3. Интерполяция функций
- •6.3.1. Постановка задачи
- •6.3.2. Интерполяционная формула Лагранжа
- •6.3.3. Интерполяционные формулы Ньютона
- •6.3.3.1. Конечные разности
- •6.3.3.2. Первая интерполяционная формула Ньютона
- •6.3.3.3. Вторая интерполяционная формула Ньютона
- •6.3.4. Сплайн – интерполяция
- •6.3.5. Сравнение интерполяционных многочленов по применению
- •6.3.6. Технология интерполяции функций в среде математических пакетов
- •Тема 6.4. Численное интегрирование
- •6.4.1. Постановка задачи
- •6.4.2. Метод прямоугольников
- •6.4.3. Формула трапеций
- •6.4.4. Формула Симпсона
- •6.4.5. Оценка погрешности численного интегрирования
- •6.4.6. Технология вычисления интегралов в среде математических пакетов
- •Тема 6.5. Методы решения обыкновенных дифференциальных уравнений
- •6.5.1. Постановка задачи
- •6.5.2. Метод Эйлера
- •6.5.3. Методы Рунге-Кутты
- •6.5.4. Решение оду n-го порядка
- •6.5.5. Сравнение методов решения оду
- •6.5.6. Технология решения обыкновенных дифференциальных уравнений средствами математических пакетов
- •6.6.2. Метод дихотомии
- •6.6.3. Метод золотого сечения
- •6.6.4. Сравнение методов
- •6.6.5. Технология решения задач одномерной оптимизации средствами математических пакетов
- •Тема 6.7. Аппроксимация функций
- •6.7.1. Постановка задачи аппроксимации
- •6.7.2. Метод наименьших квадратов
- •6.7.3. Технология решения задач аппроксимации функций средствами математических пакетов
- •Тема 6.8. Многомерная оптимизация
- •6.8.1. Постановка задачи и основные определения
- •6.8.2. Методы спуска
- •6.8.3. Метод градиентного спуска с дроблением шага
- •6.8.4. Метод наискорейшего спуска
- •6.8.5. Проблема оврагов. Метод покоординатного спуска
- •6.8.6. Технология решения задач многомерной оптимизации средствами математических пакетов
- •Список литературы
- •Тема 6.4. Численное интегрирование................................................71
- •Тема 6.5. Методы решения обыкновенных дифференциальных Уравнений............................................................................. 92
- •Тема 6.6. Одномерная оптимизация................................................ 115
- •Тема 6.7. Аппроксимация функций....................................................132
- •Тема 6.8. Методы многомерной оптимизации............................... 149
- •Список литературы.................................................................... 204
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Государственное образовательное учреждение высшего профессионального образования
Московский технический университет связи и информатики
-

12
ИНФОРМАТИКА – 4 сем.
Специальности: 210402, 210404, 2104054, 210406
Численные методы – 6 сем.
Специальность: 220301
Вычислительная математика – 6 сем.
Специальность: 230201
Раздел 6.
Учебное пособие для студентов заочного факультета
Модели и алгоритмы решения задач численными методами
использование математических пакетов
Темы 6.1 – 6.8
Москва 2011
УДК
Шакин В.Н., Семенова Т.И., Кравченко О.М. ИНФОРМАТИКА – 4 сем. Специальности: 210402, 210404, 2104054, 210406 Численные методы – 6 сем.
Специальность: 220301 Вычислительная математика – 6 сем. Специальность: 230201. Раздел 6. Учебное пособие для студентов заочного факультета: Модели и алгоритмы решения задач численными методами с использование математических пакетов использование математических пакетов использование математических пакетов
использование математических пакетов: -М., 2010.-86с.
Издание утверждено советом ОТФ-2.
Протокол №9 от 26.05.10.
Рецензенты: В.О. Мелихов, к.т.н., профессор
Г.К. Сосновиков, к.т.н., доцент
С Московский технический
университет связи
и информатики, 2010 г.
Раздел 6. Модели и алгоритмы решения задач численными методами с использованием математических пакетов Рекомендации по использованию учебного пособия
Раздел 6. Учебное пособие «Модели и алгоритмы решения задач численными методами с использованием математических пакетов» является шестым разделом учебной дисциплины «ИНФОРМАТИКА» [1]. Этот раздел включает настоящее учебное пособие и лабораторный практикум [2]. В качестве вспомогательного материала рекомендуется использовать [3,4], в котором рассмотрены базовые элементы и средства математического пакета MathCad.
Содержание данного материала соответствует стандарту подготовки специалистов по направлению 210400 – «Телекоммуникации» (дисциплина Информатика), 230200 – «Информационные системы» (дисциплина Вычислительная математика), 220300 – «Автоматизация и управление» (дисциплина Численные методы) и может быть использовано для студентов дневной, заочной и дистанционной форм обучения. Он охватывает 8 основных тем:
Элементы теории погрешностей.
Методы решения нелинейных уравнений.
Интерполяция функций.
Численное интегрирование.
Методы решения обыкновенных дифференциальных уравнений.
Одномерная оптимизация.
Аппроксимация функций.
Методы многомерной оптимизации.
Изучение каждой темы следует начинать с теоретического материала, который проиллюстрирован рисунками и примерами. В каждой теме предусмотрено рассмотрение нескольких численных методов, а в заключение приведена их сравнительная характеристика с точки зрения трудоемкости, эффективности, ограничений или универсальности применения.
После изучения теоретической части рекомендуется провести самоконтроль усвоения материала.
Тема 6.1. Элементы теории погрешностей
6.1.1. Точные и приближенные числа
6.1.2. Абсолютная и относительная погрешность
6.1.1. Точные и приближенные числа
Точность числа, как правило, не вызывает сомнений, когда речь идет о целых значениях данных (2 карандаша, 100 деревьев). Однако, в большинстве случаев, когда точное значение числа указать невозможно (например, при измерении предмета линейкой, снятии результатов с прибора и т.п.), мы имеем дело с приближенными данными.
Приближенным
значением
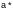 называется число, незначительно
отличающееся от точного значения
называется число, незначительно
отличающееся от точного значения
 и заменяющее его в вычислениях.
Степень отличия приближенного значения
числа от его точного значения
характеризуется погрешностью.
и заменяющее его в вычислениях.
Степень отличия приближенного значения
числа от его точного значения
характеризуется погрешностью.
Различают следующие основные источники погрешностей:
Погрешности постановки задачи, возникающие в результате приближенного описания реального явления в терминах математики.
Погрешности метода, связанные с трудностью или невозможностью решения поставленной задачи и заменой ее подобной, такой, чтобы можно было применить известный и доступный метод решения и получить результат, близкий к искомому.
Неустранимые погрешности, связанные с приближенными значениями исходных данных и обусловленные выполнением вычислений над приближенными числами.
Погрешности округления, связанные с округлением значений исходных данных, промежуточных и конечных результатов, получаемых с применением вычислительных средств.
