Неравенства Маркова и Чебышева

Н

22

еравенство Маркова. Если все значения случайной величины X неотрицательны, то вероятность того, что она примет значение, превосходящее заданное число Q > 0, удовлетворяет неравенству Маркова:

(16)

Неравенство Маркова используется при решении задач, если известно или может быть рассчитано математическое ожидание. При наличии или возможности получения информации о дисперсии следует также рассмотреть неравенства:

(17)

После сравнения результатов (16) и (17) в ответ следует записать более значимый из них.

Неравенство Чебышева. Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине превзойдет заданное положительное число , удовлетворяет неравенству:

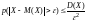- первая форма неравенства;

(18)

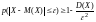- вторая форма неравенства.

Неравенство Чебышева используется при решении задач, если известна или может быть рассчитана дисперсия и искомый интервал значений случайной величины Х или возможный интервал вне искомого имеет границы симметричные относительно математического ожидания.

Неравенства Маркова и Чебышева в условиях схемы Бернулли

Здесь М(X) = np и D(X) = npq. Тогда неравенство Маркова записывается как:

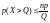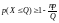- первая форма неравенства;

- вторая форма неравенства.

С учетом дисперсии:

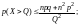
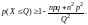
А неравенство Чебышева принимает вид:

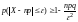- первая форма неравенства;

- вторая форма неравенства.

Если в задаче отсутствует информация о вероятностях p и q, то необходимо воспользоваться ограничением pq  0,25.

Задача 1. Среднее число телевизоров, получаемых ремонтной мастерской в течение недели, равно 10 со средним квадратическим отклонением 3. Оценить вероятность того, что в предстоящую неделю в мастерскую поступит не более 25 телевизоров.

Решение. Случайная величина X – число телевизоров, получаемых ремонтной мастерской в течение недели.

Нанесем данные задачи на числовую прямую:

10 15

x

0 а=10 25

Итак, границы интервала заданного изменения Х несимметричны относительно математического ожидания, следовательно, для решения задачи применяется неравенство Маркова (вторая форма в (16)):

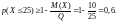
С другой стороны, известно среднее квадратическое отклонение  = 3, а тогда D(X) =  ² = 9. Используем неравенство Маркова при известной дисперсии:

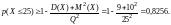
Сравнивая полученные результаты, делаем вывод: p(X  25)  0,8256.

Ответ: p(X  25)  0,8256.

З

24

адача 2. Завод отгрузил реализатору 5000 бутылок пива. Вероятность боя стеклотары в пути и при погрузочно-разгрузочных работах в целом

составляет 0,06. Оценить вероятность того, что число разбитых бутылок у реализатора превзойдет 500.

Решение. Случайная величина X – число разбитых бутылок.

Нанесем данные задачи на числовую прямую:

x

0 a=300 500 5000

Математическое ожидание и дисперсия находятся по формулам a = np и D(X) = npq, так как задача относится к задачам на схему Бернулли. Итак, a = 50000,06 = 300; D(X) = 50000,060,94 = 282.

Используем неравенство Маркова в условиях схемы Бернулли:

Сравнивая результаты, делаем вывод: p(X > 500)  0,3611.

Ответ: p(X > 500)  0,3611.

Задача 3. Среднее число автобусов автопарка, отправляемых в ремонт после месяца эксплуатации, равно 10 при среднем квадратическом отклонении 4 автобуса. Оценить вероятность того, что в течение месяца автопарк отправит в ремонт от 5 до 15 машин включительно.

Решение. Х – число автобусов, отправляемых в ремонт.

Нанесем данные задачи на числовую прямую:

5 5

x

0 5 a=10 15

Известно, что  = 4, а, следовательно, D(X) =  ² = 16; интересуемый интервал значений Х симметричен относительно математического ожидания этой случайной величины, поэтому воспользуемся неравенством Чебышева (второй формой в (18)):

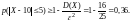
Ответ: p(|X – 10|  5)  0,36.

Задача 4. Вероятность задержки рейса самолета по техническим причинам равна 0,03. Оценить вероятность того, что из 1200 планируемых в

течение месяца вылетов из аэропорта произойдет по этим причинам задержка более 72 рейсов.

Решение. X – число задержек вылетов самолетов в месяц.

Нанесем данные задачи на числовую прямую:

36 36

x

0 a=36 72 1200

Математическое ожидание и дисперсия находятся по формулам a = np и D(X) = npq, так как задача относится к задачам на схему Бернулли. Итак, a = 12000,03 = 36, D(X) = 12000,030,97 = 34,92.

Дисперсия известна, а также интервал значений случайной величины Х вне искомого имеет границы, симметричные относительно математического ожидания а = 36, следовательно, используем для решения задачи неравенство Чебышева в условиях схемы Бернулли:

p(X > 72) = 1 – p(X  72) = 1 – p(|X – 36|  36)  1 – =

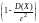= 34,92/ 36 ² = 0,0269.

Ответ: p(X > 72)  0,0269.