Отклонение относительной частоты от вероятности

Вероятность того, что абсолютная величина отклонения относительной частоты появления события от вероятности появления события в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1) не превысит положительного числа , приближенно равна удвоенной функции Лапласа при

= 2 (4)

Задача 1. Вероятность выигрыша по билету лотереи равна 1/7. Найти вероятность выиграть: а) по двум билетам из шести; б) не менее чем по двум билетам из шести.

10

Решение. Событие А = {выиграть по билету лотереи}, Так как n = 6, то используется формула Бернулли.

а) Пусть событие В = {выиграть по двум билетам из шести}:

б) Пусть событие С = {выиграть не менее чем по двум билетам из шести}: Получается сложная формула для вычисления вероятности. С другой стороны, используя противоположное событие,

Ответ: а) р(В) = 0,165; б) р(С) = 0,207.

Задача 2. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах число поражений мишени будет: а) равно 73; б) находится между 80 и 95.

Решение. Событие А = {поражение мишени}, р = р(А) = 0,8; q = 0,2. Так как n = 100, то необходимо найти npq = 1000,80,2 = 16 > 9. Следовательно, используется формула Муавра-Лапласа.

а) Локальный случай:

где

То есть

Значение функции определяется по таблице №1 Приложений.

б) Интервальный случай:

= (x₂) – (x₁), где ;

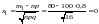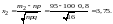
То есть, р₁₀₀(80; 95) = (3,75) – (0) = 0,4995 – 0 = 0,4995.

Значение функции (x) определяется по таблице №2 Приложений.

Ответ: а) р₁₀₀(73) = 0,022; б) р₁₀₀(80; 95) = 0,4995.

Задача 3. В среднем левши составляют 1%. Найти вероятность того, что в аудитории из 200 студентов окажется: а) ровно 2 левши; б) не менее чем 4 левши; в) хотя бы 1 левша.

Решение. Событие А ={студент – левша}, р = р(А) = 0,01; q = 0,99. Так как n = 200, то найдем npq = 2000,010,99 = 2 < 9. Следовательно, используется формула Пуассона.

а) Локальный случай:

Значение функции е ^–х определяется по таблице №3 Приложений.

б) Интервальный случай:

в) Интервальный случай:

.

Ответ: а) р₂₀₀(2) = 0,27; б) р₂₀₀( 4) = 0,14; в) р₂₀₀( 1) = 0,864.

Задача 4. Для данного баскетболиста вероятность забросить мяч в корзину при броске равна 0,4. Произведено 30 бросков. Найти наивероятнейшее число попаданий и соответствующую вероятность.

Решение. Событие А = {мяч заброшен в корзину}, р = р(А) = 0,4; q = 0,6; n = 36; npq = 7,2.

Найдем наивероятнейшее число из двойного неравенства

. Подставив данные задачи, получим

30∙0,4 – 0,6  m₀  30·0,4 + 0,4 или 11,2  m₀  12,4.

Так как m₀ – целое число, то m₀ = 12.

Поскольку npq = 7,2 < 9, то, используя локальную формулу Муавра-Лапласа, найдем где

Тогда

Ответ: m₀ = 12, р₃₀(12) = 0,1487.

Задача 5. Сколько нужно провести опытов, чтобы с вероятностью 0,901 утверждать, что частота интересующего нас события будет отличаться по абсолютной величине от вероятности появления этого события, равной 0,4, не более чем на 0,1?

Решение. По условию р = 0,4; q = 0,6;  = 0,1;

Воспользуемся формулой (4): 2 или



По таблице №2 Приложений значение аргумента х = 1,65. Следовательно, 0,204 или , n = 65,42.

Таким образом, искомое число испытаний n = 66.

Ответ: n = 66.