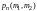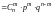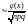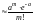Формула полной вероятности и формула Байеса

Пусть гипотезы В₁, В₂, …, В_n образуют полную группу событий и попарно несовместны, а событие A может наступить лишь в результате осуществления одной из гипотез . Тогда вероятность события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

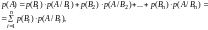(2)

где p(В₁) + p(В₂)+…+ p(В_n) = 1.

Допустим, произведено испытание, в результате которого появилось событие А. Вероятности гипотез В_i после опыта, т.е. условные вероятности: р(А/В₁), р(А/В₂), …, р(А/В_n), вычисляются по формуле Байеса:

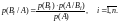(3)

Эта формула позволяет оценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Задача 1. После вакцинирования животное в период эпидемии заболевает с вероятностью 0,01, а не вакцинированное – 0,8. Вакцинировано 70% животных. Найти вероятность того, что во время эпидемии животное заболеет.

Решение. Обозначим событие А = {животное заболеет}. Возможны следующие гипотезы: В₁ = {животное вакцинировано}, В₂ = {животное не вакцинировано}. Гипотезы В₁, В₂ несовместны и образуют полную группу событий. По условию задачи вероятности этих гипотез: р(В₁) = 0,7, р(В₂) = 0,3. Условная вероятность того, что животное заболеет, если оно вакцинировано р(В₁/ А) = 0,01, а условная вероятность того, что животное заболеет, если оно не вакцинировано р(В₂/ А) = 0,8.

Вероятность события А определяется по формуле полной вероятности:

р(А) = р(В₁)·р(В₁/ А) + р(В₂)·р(В₂/ А) = 0,7·0,01 + 0,3·0,8 = 0,247.

Ответ: р(А) = 0,247.

Задача 2. В ящике содержится 12 деталей завода №1, 20 деталей завода №2, 18 деталей завода №3. Завод №1 выпускает 90% продукции отличного качества, завод №2 – 60%, а завод №3 – 80% продукции отличного качества. Извлеченная наудачу из ящика деталь оказалась отличного качества. Найти вероятность того, что она изготовлена на заводе №2.

Решение. Обозначим событие А ={наудачу взятая из ящика деталь окажется отличного качества}. Возможны следующие гипотезы: В₁ = {деталь изготовлена на i-м заводе}, 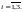Гипотезы В₁, В₂, В₃ попарно несовместны и образуют полную группу событий. Поскольку в ящике всего 22+20+18 = 50 деталей, то по классической формуле вероятности:

Условные вероятности того, что деталь окажется отличного качества, если она изготовлена на i-м заводе (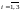 ) по условию задачи равны:

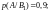
По формуле полной вероятности (2):

р(А) = 0,24∙0,9 + 0,4∙0,6 + 0,36∙0,8 = 0,744.

По формуле Байеса (3) найдем вероятность того, что извлеченная деталь изготовлена на заводе №2:

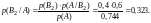
Ответ: р(В₂ /А) = 0,323.

Схема Бернулли

Вероятность события в условиях схемы Бернулли

Несколько испытаний называются независимыми, если вероятность того или иного исхода в любом из этих испытаний не зависит от исхода других испытаний.

Схема Бернулли: производится n независимых испытаний, в каждом из которых с одной и той же вероятностью p наступает некоторое событие А и, следовательно, с вероятностью q = 1 – p наступает событие 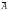, противоположное А.

Обозначим через 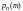вероятность того, что в n испытаниях схемы Бернулли событие А наступит m раз ( ).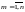

Справедливы следующие формулы:

n	npq	Локальная вероятность	Интервальная вероятность
 10	для всех npq	(формула Бернулли)
 10	> 9	(локальная формула Муавра-Лапласа)	 (x2) – (x1) (интегральная формула Муавра-Лапласа)
	 9	(формула Пуассона)

где a = np – математическое ожидание числа появления события A в n испытаниях в условиях схемы Бернулли;

, функция стандартного распределения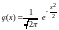 – четная табулированная функция (то есть, 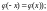нормированная функция Лапласа (x) = 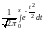– нечетная табулированная функция (то есть, (–x) = – (x)); – вероятность того, что при n испытаниях в условиях схемы Бернулли событие А наступит ровно m раз; – вероятность того, что при n испытаниях в условиях схемы Бернулли событие А наступит не менее m₁ раз и не более m₂ раз, то есть

Справедливы также следующие формулы:

Наивероятнейшее число m₀ появления события А в n испытаниях в условиях схемы Бернулли определяется из: 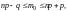где m₀ – целое число.