Министерство образования и науки Российской Федерации

Сочинский государственный университет туризма и курортного дела

Н.С. Абуева, И.Л. Макарова,

В.И. Самарин, Н.Ф. Якунина

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методические указания по выполнению контрольных работ для студентов зфо экономических специальностей

Сочи – СГУТиКД

2004

УДК 519.21

ББК 22.17я73

Представлено кафедрой прикладной математики ИИТиМ

Рекомендовано к печати Ученым советом Института информационных технологий и математики СГУТиКД

Абуева Н.С., Макарова И.Л., Самарин В.И., Якунина Н.Ф.

Теория вероятностей и математическая статистика: Методические указания по выполнению контрольных работ для студентов ЗФО экономических специальностей. – Сочи: СГУТиКД, 2004. –

56 с.

Указания содержат основные определения, правила, теоремы и формулы, необходимые для решения простейших задач по теории вероятностей и математической статистике, а также варианты контрольных заданий.

УДК 519.21

ББК 22.17я73

Лицензия лр № 022330 от 30.03.99. Авторская редакция.

Подписано в печать . . 2004. Формат 60х84/16. Бумага офсетная.

Гарнитура шрифта Таймс. Печать трафаретная. Уч.-изд. л. 3,2. Тираж 200 экз. Заказ №

Отпечатано с готового оригинал-макета.

г. Краснодар

© Н.С. Абуева, И.Л. Макарова, В.И. Самарин, Н.Ф. Якунина, 2004

© СГУТиКД, 2004

Расчет вероятности события

Классическое определение вероятности

При классическом определении вероятность события определяется равенством

р(A)=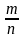 , (1)

где m – число исходов проводимого опыта, благоприятствующих появлению события А; n – общее число возможных исходов.

Основные элементы комбинаторики

Пусть даны 2 множества:

{а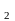 , а ,…, а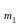 } и {b , b ,…,b }.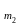

Правило суммы: Если объект типа «а» может быть выбран m₁ способами, а объект типа «b» – m₂ способами, то выбор или «а», или «b» может быть осуществлен N = m₁ + m₂ способами.

Правило произведения: Если объект типа «а» может быть выбран m₁ способами, и после любого такого выбора объект «b» может быть выбран m₂ то выбор и «а», и «b» можно осуществить N = m₁·m₂ способами.

Основной принцип комбинаторики: Если имеется k множеств, причем из каждого можно составить комбинации соответственно n₁, n₂,…, n_k способами, то комбинация, содержащая комбинации по одной из исходных множеств, может быть составлена N = n₁·n₂·…·n_k способами.

Определение 1. Сочетаниями из n различных элементов по m, причем m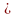 n, называются такие комбинации, каждая из которых содержит ровно m элементов и отличается от любой другой хотя бы одним элементом. Число сочетаний из n элементов по m элементов обозначается С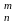 и находится по формуле

С = ,

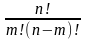где n!, m!, (n – m)! – факториалы, то есть произведения соответственно n, m, n – m последовательных натуральных чисел, начиная с 1, например, 5! = 1·2·3·4·5 = 120. По определению 0! = 1.

Задача 1. В лотерее разыгрывается 100 билетов; из них 10 являются выигрышными, а остальные 90 – «пустые». Некто покупает 5 билетов. Какова вероятность, что среди них будет 2 выигрышных и 3 «пустых».

Решение. Событие А = {среди 5 отобранных билетов 2 выигрышных и 3 «пустых»}.

Д

ля наглядности решения задачи составим схему взаимосвязанных множеств:

Всего Выигрышные Пустые

100 = 10 + 90

↓ ↓ ↓

5 = 2 + 3

Согласно (1) вероятность события А определяется как p(А) = . Общее число n возможных различных способов отбора равно числу способов, которыми можно отобрать 5 билетов из 100: n = C .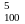

Число исходов m, благоприятствующих событию А, зависит от двух условий: среди отобранных билетов должно оказаться 2 выигрышных и 3 «пустых». Число различных способов отбора двух выигрышных билетов из 10 возможных: m₁ = C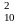 ; а число различных способов отбора трех «пустых» билетов из 90: m₂ = C . Используя правило произведения, получаем: m = m₁·m₂ – число способов, благоприятствующих событию А. Следовательно, искомая вероятность

p(A)= = 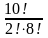· 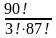: 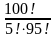≈ 0,07.

Ответ: p(A) ≈ 0.07.