Расчетная схема замещения

Для расчета режимов работы трансформатора как элемента электрической цепи (определения токов и напряжений при различной нагрузке), нужна расчет­ная математическая модель. Она должна быть достаточно простой, но одновременно должна позволять с необходимой точностью определять основные электрические параметры трансформатора. Проще всего эту модель строить на основе расчетной схемы замещения трансфор­матора.

Для рассмотренного выше идеального трансформатора эта схема содержит в первичной обмотке источник питающего напряжения и источник индуцированной ЭДС, а во вторичной – источник индуцированной ЭДС и приемник. Схе­ма приведена на рис. 5.

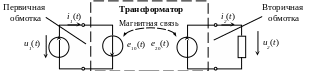
Рис. 5. Схема замещения идеального трансформатора

Для неидеального трансформатора необходимо учесть нагрев проводников обмоток и ЭДС (индуктивностей) от потоков рассеяния. В результате схема замещения идеализированного трансформатора примет вид, показанный на рис. 6.

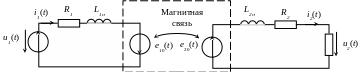
Рис. 6. Схема замещения идеализированного трансформатора

Для схемы рис. 6 можно записать уравнения по второму закону Кирхгофа

,

.

Наличие магнитной связи в схеме усложняет расчет. Поэтому с помощью эквивалентных преобразований магнитную связь можно заменить гальваничес­кой (то есть связь посредством токов). Для этого нужно левую и правую часть уравнения вторичной обмотки умножить на коэффициент трансформации (n₁/n₂):

.

Здесь .

Важно, что после преобразования в уравнение входит такая же ЭДС e₁₀(t), как и в первичной обмотке. Введем следующие обозначения:

(5)

, , , .

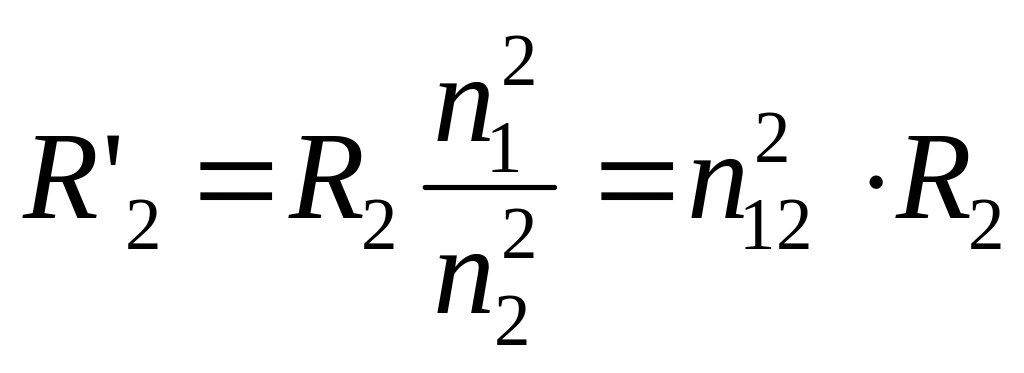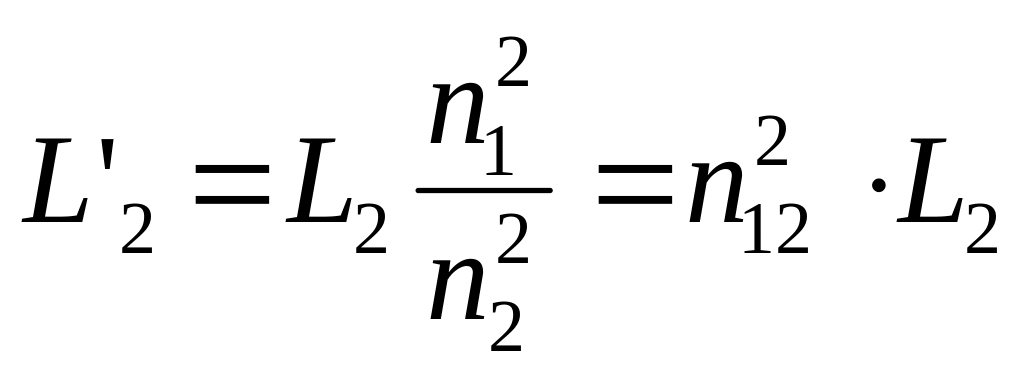Величины со штрихами, относящиеся к вторичной катушке, называются «приведенные к первичной обмотке», например, i¢₂(t) – приведенный ток, L¢_2– приведенная индуктивность от потока рассеяния и т.п.

Теперь уравнения "приведенного трансформатора" примут вид:

,

.

Э ти уравнения справедливы при любых напряжениях питания u₁(t). Для синусоидального напряжения в комплексном виде (используем символический метод) эти уравнения можно записать так:

(6)

Последнее слагаемое в этих уравнениях может рассматриваться как индуктивное сопротивление, в котором ток равен сумме тока первичной и приведенного тока вторичной обмотки. Этим уравнениям соответствует расчетная схема замещения приведенного трансформатора рис. 7. Эта схема используется для расчетов токов и напряжений в различных режимах работы трансформатора: холостого хода, режима нагрузки и короткого замыкания.

Рис. 7. Расчетная схема замещения приведенного трансформатора

С

(7)

овременные трансформаторы конструируются так, что практически всегда выполняются приближенные равенства:

и .

Эти условия позволяют рассчитывать параметры трансформатора по каталожным данным.

Каталожные данные трансформаторов

Для уменьшения массогабаритных показателей катушки трансформаторов помещают на замкнутый ферромагнитный сердечник (его называют "магнитопровод"). При этом магнитный поток, вообще говоря, зависит от тока нелинейно , поскольку магнитное сопротивление ферромагнетика существенно зависит от тока (с учетом гистерезиса). Эта нелинейность приводит к нагреву сердечника при его перемагничивании, то есть возникают потери энергии на нагрев сердечника. Для учета этих потерь в схему замещения добавляют активное сопротивление R_m, включенное параллельно индуктивному сопротивлению взаимной индукции (×n₁₂×M).

Каталожными называются номинальные (то есть, на которые трансформаторы проектируются) данные трансформаторов и данные опытов холостого хода и короткого замыкания.

К номинальным данным относятся:

• номинальное первичное U_1ном и номинальное вторичное U_2ном напряжения (их действующие значения);

• для трехфазных трансформаторов приводится схема соединения фаз первичной и вторичной обмоток (в звезду, в треугольник).

• номинальная полная мощность S_ном;

• массогабаритные показатели (в расчетах режимов работы массогабаритные показатели не используются)

К каталожным данным относятся:

• номинальные данные (см. выше);

• напряжение короткого замыкания u_К% ;

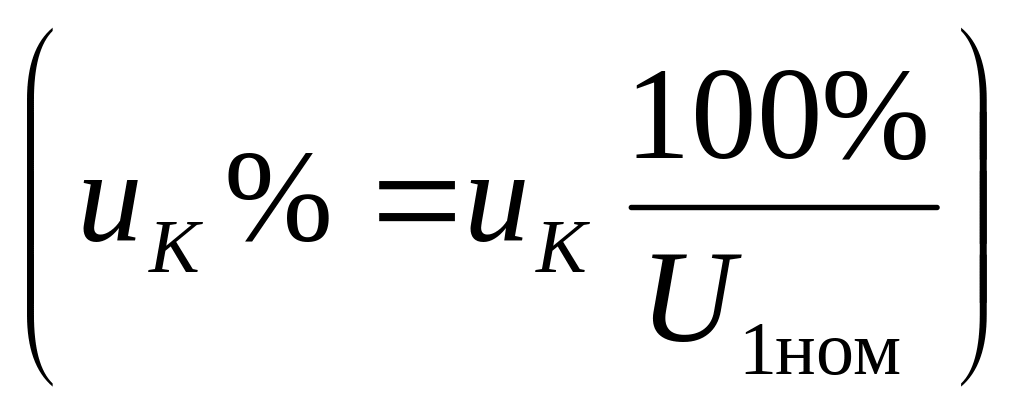• ток холостого хода I_XX% ;

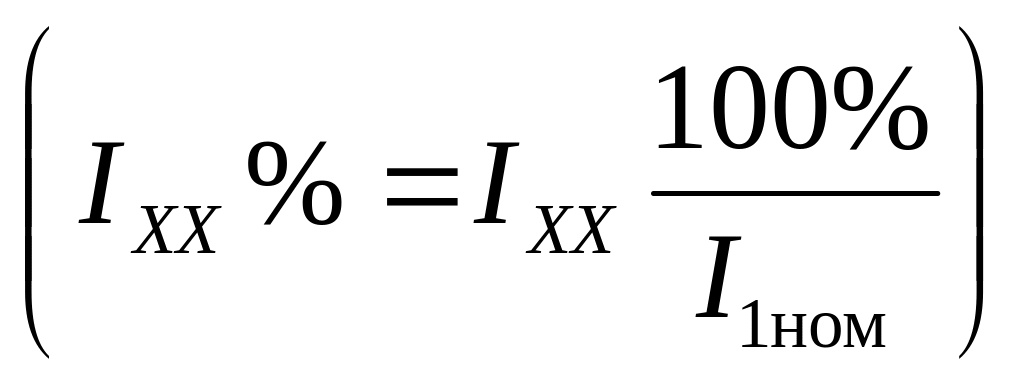• мощность потерь холостого хода Р₀;

• мощность потерь короткого замыкания Р_К.

На основе схемы рис. 7 можно получить основные расчетные соотношения, включающие номинальные и каталожные данные трансформаторов.

Режим холостого хода

Это режим работы трансформатора при разомкнутой вторичной обмотке, то есть при i₂(t) = 0.

На рис. 8 приведена схема трансформатора в режиме холостого хода.

Рис. 8. Схема замещения приведенного трансформатора в режиме холостого хода

_{Уравнения трансформатора в режиме холостого хода:}

Переходя от комплексных чисел к модулям, получим:

_;

Отсюда можно найти

(8)

_.

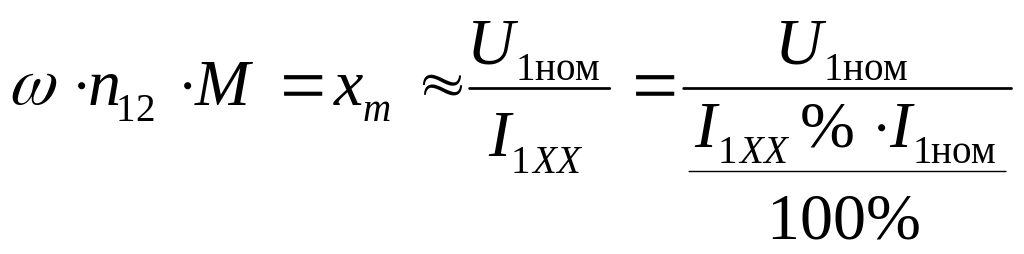
Сопротивление x_m называется индуктивным сопротивлением от общего маг­нитного потока.

Номинальный ток может быть определен по номинальным данным с помо­щью формул:

д

(9а)

ля однофазных трансформаторов ,

д

(9)

ля трехфазных трансформаторов – .

Мощность потерь холостого хода определяет в основном нагрев ферромаг­нитного сер­деч­ника трансформатора и не влияет на основные электрические параметры схемы замещения трансформатора и поэтому в расчетах, как правило, не используется.

Если требуется учесть потери энергии на нагрев сердечника, то сопротивление R_m можно рассчитать по формуле:

.

Опыт короткого замыкания

Это режим работы трансформатора при пониженном напряжении первичной катушки и при замкнутой вторичной обмотке накоротко, то есть при u₂(t) = 0. При этом к первичной обмотке трансформатора подводится напряжение, которое называется "напряжение короткого замыкания". Оно выбирается так, чтобы в обмотках были номинальные токи.

На рис. 9,а приведена схема замещения трансформатора не в опыте, а в ре­жи­ме короткого замыкания, когда напряжение питания не понижено, а равно номинальному. Такой режим является аварийным, поскольку токи в обмотках во много раз могут превысить номинальные и тран­сформатор может выйти из строя из-за перегрева.

На рис. 9,б приведена схема замещения трансформатора в опыте короткого замыкания, когда напряжение питания равно такому напряжению короткого замыкания, при котором токи в обмотках равны номинальным.

На рис. 9,в приведена расчетная схема замещения трансформатора в опыте короткого замыкания, где учтены приближенные равенства (7).

Уравнения в режиме короткого замыкания имеют вид:

_,

_.

Отсюда

и

.

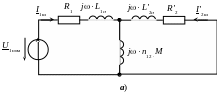
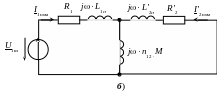
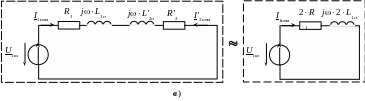
Рис. 9. Схема замещения трансформатора в режиме (а) и опыте (б) короткого замыкания, расчетная схема замещения в опыте короткого замыкания (в)

По каталожным данным в опыте короткого замыкания можно найти:

(10)

, ,

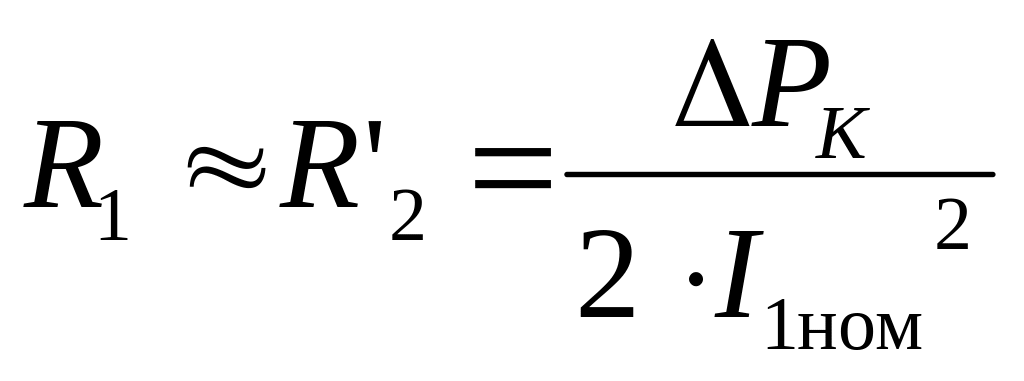
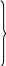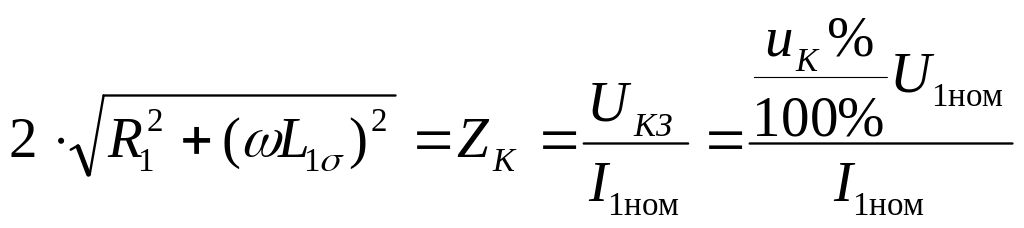Таким образом, соотношения (8 – 10) позволяют определить параметры элементов расчетной схемы замещения трансформатора по каталожным данным. Знание параметров элементов схемы замещения позволит рассчитать любой режим работы трансформатора: от холостого хода до короткого замыкания.

Пример расчета трансформатора

Требуется определить параметры расчетной схемы замещения мощного трех­фаз­ного трансформатора ТСЗ-630/10, имеющего следующие каталожные данные:

- номинальная мощность трансформатора S_HOM = 630 кВА;

- номинальное напряжение обмотки высшего напряжения (ВН) U_1ном = 10,5 кВ;

- номинальное напряжение обмотки низшего напряжения (НН) U_2ном = 0,4 кВ;

- напряжение короткого замыкания u_K % = 5,5 %;

- мощность потерь холостого хода P₀ = 2000 Вт;

- мощность потерь короткого замыкания P_K = 7300 Вт;

- ток холостого хода I₀% = 1,5 %.

- габариты: длина 2,25 м; ширина 1,1 м; высота 2,3 м; масса 3400 кг.

По (9) найдем номинальный ток первичной обмотки (ВН)

А, а по (8) можно рассчитать индуктивное сопротивление от общего магнитного потока

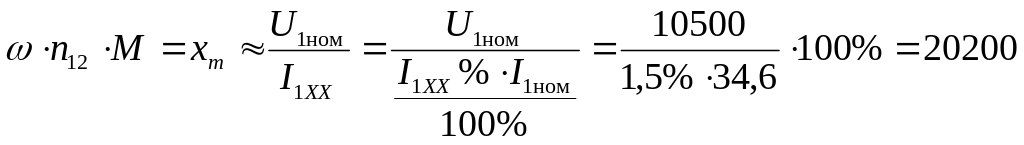_{, Ом.}

По (10) можно найти остальные параметры:

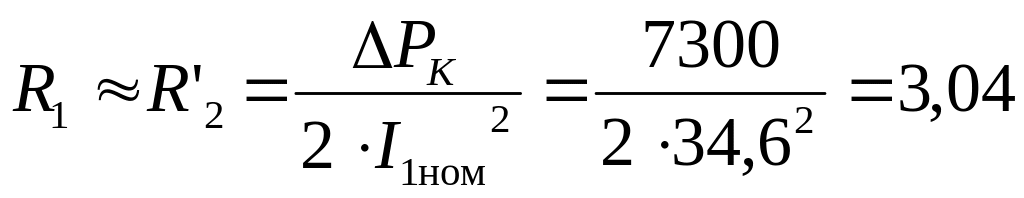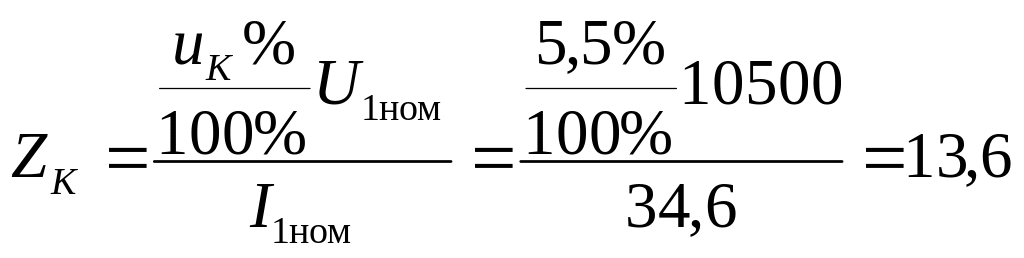, Ом; , Ом,

, Ом.

Коэффициент трансформации трансформатора равен

.

Полученные параметры расчетной схемы замещения трансформатора поз­воляют рассчитывать режим нагрузки трансформатора.

Например, пусть активная мощность нагрузки Р_нагр составляет 430 кВт, а коэффициент мощности cos_нагр ра­вен 0,74. Номинальное напряжение нагрузки U_нагр равно 380 В. Определим напряжение на вторичной обмотке в режиме нагрузки трансформатора.

Для схемы рис. 7 можно записать с учетом закона Ома

,

.

Откуда после несложных преобразований получим

.

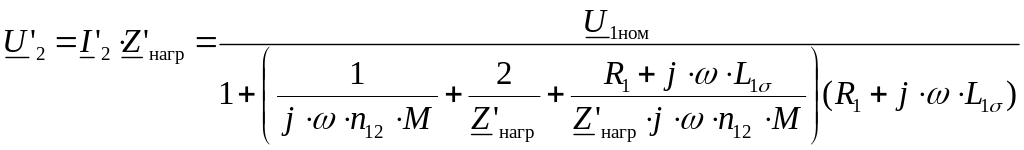Здесь

, , отсюда

А.

= 0,184 +j0,167 Ом.

Приведенное сопротивление нагрузки равно

Ом.

С учетом этих значений, имеем приведенное напряжение вторичной обмотки

, В.

Неприведенное напряжение равно , В. Модуль напряжения приближенно равен 372 В, то есть меньше номиналь­ного на

,

что не выходит за пределы допустимого отклонения напряжения (по российским стандартам для электроприемников)

–5% < U% < +10%.

Внешняя характеристика трансформатора

Для построения внешней характеристики трансформатора определяют из­ме­нение напряжения, под которым понимается арифметическая разность между вторичными напряжениями трансформатора при холостом ходе и при номинальном токе нагрузки.

Изменение напряжения представляет собой важную эксплуатационную ха­рактеристику трансформатора. Проще всего его определить с помощью век­тор­ной диаграммы для схемы рис.7, когда пренебрегают током намагничива­ния I₁+I '₂  0. В результате получается схема, приведенная на рис. 10.

О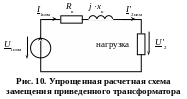 собенностью схемы являются не произвольные, а номинальные зна­чения токов. Для удобства последующего анализа комплексный ток I'_2ном принят с противоположным зна­ком.

Соответствующая векторная ди­аграмма приведена на рис.11,а.

Здесь напряжение короткого замыкания представлено двумя составляющими:

,

.

Хотя изменение напряжение равно

или

,

на вектор­ной диаграмме изменением нап­ряжения считают не отрезок CD', а отрезок CD. Погрешность при этом невелика. Из рис. 11,а следует

.

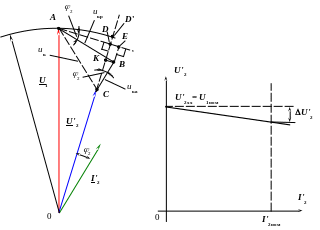
а) б)

Рис. 11. Упрощенная векторная диаграмма (а) и внешняя характеристика трансформатора (б)

Таким образом, изменение напряжения в трансформаторе равно

или . (11)

Если необходимо определить изменение нап­ряжения при токе I₂  I_2ном, то достаточно умножить правую часть (11) на коэффициент нагрузки трансформатора .

На рис. 11,б приведена внешняя характеристика тра­нсформатора, где показано изменение напряжения. Характеристика считается прямой линией и проводится через две точки с координатами: [0; U_1ном] и [I'_2ном; (U_1ном – U'₂)].

Теоретические положения к задаче 3.2

Э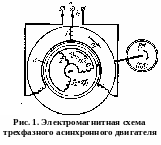 лектромагнитная схема наиболее распространенного трехфаз­ного асинхронного двигателя представлена на рис.1¹. Она отличается от схемы трансформатора тем, что ее магнитная система выполнена (из листовой электротехнической стали) в виде двух концентрических цилинд­ров, из которых внутренний (ротор), укрепляемый на валу в подшипни­ках, может свободно вращаться внут­ри неподвижного внешнего (статора). Обмотка 1 размещается равномер­но по окружности статора так, чтобы отдельные ее фазы были сдвинуты по отношению друг к другу на 120°. Обмотка 2 на роторе выполняется трехфазной или многофазной и в про­стейшем случае замыкается накорот­ко. Для лучшей магнитной связи воздушный зазор 3 между статором и ротором выбирается минимально возможным. Если обмотку статора присоединить к источнику трехфаз­ного тока, то ток, протекая по обмот­ке, создаст магнитное поле, ось кото­рого непрерывно перемещается (вра­щается) в пространстве (рис.2,а)². Это вращающееся поле будет наво­дить токи в замкнутой обмотке ро­тора, которые, взаимодействуя с по­лем, создадут электромагнитные си­лы, стремящиеся двигать ротор в на­правлении вращения поля. Послед­нее легко уяснить себе из простей­шей модели (рис.2,б).

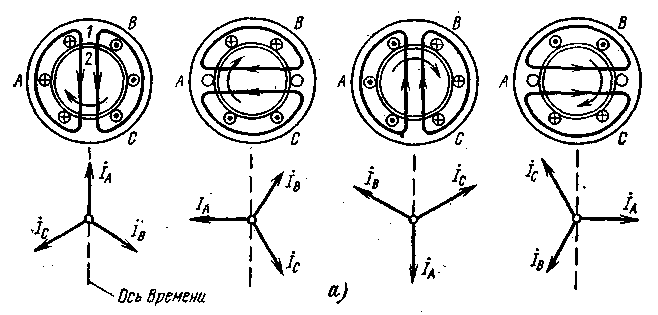
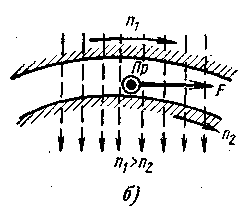
Рис. 2. Объяснение принципа работы трехфазного асинхронного двигателя: а – образование вращающегося магнитного поля; б – взаимодействие тока ротора с магнитным полем при работе машины двигателем

При движении магнитного поля, например слева направо, в провод­нике Пр ротора возникает ЭДС, направленная из-за плоскости чер­тежа (правило «правой руки»). Если ток в проводнике будет при этом совпадать по фазе с ЭДС, то дей­ствующая на проводник электромаг­нитная сила F будет стремиться двигать его в направлении вращения поля (правило «левой руки»).

Ротор двигателя, основанного на этом принципе, будет вращаться всег­да медленнее поля (асинхронно по отношению к последнему), так как только при этих условиях в обмотке ротора наводятся ЭДС и проте­кают токи. Это отставание ротора от поля называют скольжением. Чем больше скольжение, тем боль­шие токи возникают в обмотке ротора (при заданном неизменном магнитном поле) и тем большее механическое сопротивление способен преодолевать ротор, вращая рабочий механизм РМ (рис. 1). Таким образом, частота вращения асинхронного двигателя меняется с нагрузкой, постепенно уменьшаясь с ростом последней.

Если вращающееся магнитное по­ле, создаваемое переменным током, образует на окружности статора один северный (С) и один южный (Ю) полюсы (т. е. одну пару полюсов), то в этом простейшем случае одному периоду переменного тока соответст­вуют поворот оси поля на 360° и возвращение ее в исходное положе­ние (рис. 2,а). Если обозначить число оборотов поля в минуту через п₁, то число его оборотов в секунду будет п₁ / 60 и, следовательно, или , где f₁ – частота тока статора, со­здающего поле.

Если обмотку статора выполнить так, что число пар полюсов магнит­ного поля вдоль окружности воздуш­ного зазора будет р, то частота вра­щения магнитного поля, так назы­ваемая «синхронная частота враще­ния», при той же частоте будет в р раз меньше, так как ось магнитного поля повернется на 360° теперь за р периодов; поэтому в общем случае

(1)

или

(2)

Скольжение ротора асинхронного двигателя s в долях синхронной частоты вращения п₁ равно:

(3)

Частота ЭДС и токов ротора может быть найдена из равенства, аналогичного (2), если вместо п₁ подставить частоту вращения поля относительно ротора, т. е. п₁ – п₂ = sn₁, тогда

. (4)

Из (3) с учетом (4)

(5)

Обычно при работе асинхронной машины s << 1, поэтому, как следует из равенства (5), ее ротор вращается с частотой, близкой к синхронной, лишь незначительно снижая частоту вращения с нагрузкой.

Из-за своей простоты и надеж­ности трехфазный асинхронный дви­гатель нашел широкое распростране­ние в установках переменного тока.

Как всякая электрическая ма­шина, асинхронная машина обра­тима, т. е. она может работать как в режиме двигателя, так и в режиме генератора, преобразуя механиче­скую энергию переменного тока. В ре­жиме генератора ротор машины надо вращать приводным двигателем ПД быстрее поля (n₂ > n₁). При этом изме­няются направления наведенных в обмотке ротора ЭДС и тока, а следователь­но, и направле­ние тока в статоре³. При этих усло­виях машина уже не потребляет, а отдает в сеть активную мощность соответственно механической мощ­нос­ти, затрачиваемой приводным дви­гателем на вращение ротора (электро­магнит­ная сила F в режиме генератора меняет свое направле­ние и противо­действует вращению ротора).

Как было показано выше, основ­ной особенностью асинхронной маши­ны является чисто магнитная транс­форматорная связь между обмотками первичной и вторичной систем. Изме­нение тока в первичной системе свя­зано с изменением тока во вторичной системе. Поэтому дальнейшим разви­тием электромагнитной схемы электрической машины является раздель­ное питание обмоток статора и ротора.

Номинальную мощность на зажимах двигателя определяют по формуле:

P_1ном = Р_2ном /, кВт,

здесь КПД  следует подставлять в относительных единицах.

Номинальные фазные напряжения при соединении обмоток статора звездой и треугольником определяют исходя из соотношения между линей­ными и фазными напряжениями при звезде и треугольнике (линейные напряжения заданы).

Номинальные линейные токи определяют из формулы мощности на зажимах двигателя:

.

Фазные токи определяют исходя из соотношений между фазными и ли­нейными токами при звезде и треугольнике.

Пусковой ток двигателя определяют, используя кратность пускового тока (см. табл. 3.2) и значения номинальных токов при соединении в звезду и треугольник.

Номинальный вращающий момент двигателя М_ном (в Нм) определяют по формуле:

Здесь Р_2ном в кВт, n_2ном в об/мин.

Зная номинальный момент М_ном и кратность пускового момента К_пуск (см. табл. 3.2) можно определить пусковой момент М_пуск.

Максимальный вращающий момент М_max определяют аналогично, используя М_ном и К_max.

Характеристику М = f(s) рассчитывают по упрощенной формуле Клосса:

,

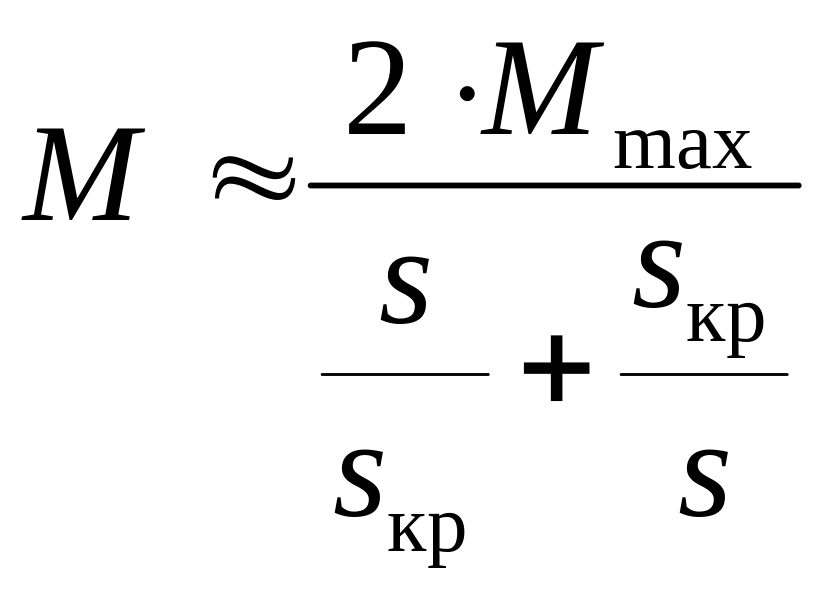где s_кр - критическое скольжение, при котором двигатель развивает максимальный вращающий момент:

Механическая характеристика М = f(s) показана на рис. 3.

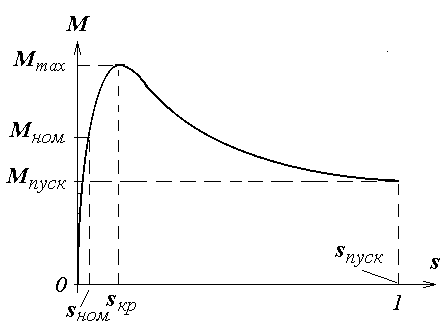
Рис. 3