6.1 Определение ошибки репрезентативности

Определение средней ошибки средней (или относительной) величины (ошибки репрезентативности) — m

Ошибка репрезентативности (m) является важнейшей статистической величиной, необходимой для оценки достоверности результатов исследо­вания. Эта ошибка возникает в тех случаях когда требуется по части оха­рактеризовать явление в целом. Эти ошибки неизбежны. Они проистекают из сущности выборочного исследования; генеральная совокупность может быть охарактеризована по выборочной совокупности только с некоторой погрешностью, измеряемой ошибкой репрезентативности.

Ошибки репрезентативности нельзя смешивать с обычным представлени­ем об ошибках: методических, точности измерения, арифметических и др.

По величине ошибки репрезентативности определяют, насколько ре­зультаты, полученные при выборочном наблюдении, отличаются от ре­зультатов, которые могли бы быть получены при проведении сплошного исследования всех без исключения элементов генеральной совокупности.

Этот единственный вид ошибок, учитываемых статистическими мето­дами, которые не могут быть устранены, если не осуществлен переход на сплошное изучение. Ошибки репрезентативности можно свести к доста­точно малой величине, т. е. к величине допустимой погрешности. Делается это путем привлечения в выборку достаточного количества наблюдений (n).

Каждая средняя величина — М (средняя длительность лечения, сред­ний рост, средняя масса тела, средний уровень белка крови и др.), а также каждая относительная величина — Р (уровень летальности, заболеваемо­сти и др.) должны быть представлены со своей средней ошибкой — m. Так, средняя арифметическая величина выборочной совокупности (М) имеет ошибку репрезентативности, которая называется средней ошибкой средней арифметической (mM) и определяется по формуле:

mM =	
	√ n

Как видно из этой формулы, величина средней ошибки средней ариф­метической прямо пропорциональна степени разнообразия признака и об­ратно пропорциональна корню квадратному из числа наблюдений. Следовательно, уменьшение величины этой ошибки при определении степени разнообразия () возможно путем увеличения числа наблюдений.

На этом принципе основан метод определения достаточного числа на­блюдений для выборочного исследования.

Относительные величины (Р), полученные при выборочном исследо­вании, также имеют свою ошибку репрезентативности, которая называется средней ошибкой относительной величины и обозначается тр.

Для определения средней ошибки относительной величины (Р) ис­пользуется следующая формула:

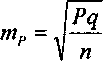
где Р — относительная величина. Если показатель выражен в процен­тах, то q = 100 - Р, если Р — в промиллях, то q=1000 - Р, если Р—в продецимиллях, то q=10 000 - Р и т.д.; n — число наблюдений. При числе на­блюдений менее 30 в знаменатель следует взять n - 1.

Примеры определения средних ошибок средних и относительных величин

mM =  √ n
У 49 больных гипертиреозом исследован уровень пепсина n=49 М=1.0 г%  = 0,35 г% mм =? mм = 0,35 = ± 0,05г% √49	Исследовано 110 больных с абсцес­сом легкого, из них у 44 обнаруже­ны дистрофические изменения пародонта n=110 Р = 44*100 = 40% 110 лиц с дистрофиче­скими изменениями пародонта q= 100 - 40=60% лиц без дистрофи­ческих изменений пародонта mр=? mр= √ 40*60 = ± 4,7% 110

Каждая средняя арифметическая или относительная величина, полу­ченная на выборочной совокупности, должна быть представлена со своей средней ошибкой. Это дает возможность рассчитать доверительные грани­цы средних и относительных величин, а также определить достоверность разности сравниваемых показателей (результатов исследования).