Основные числовые характеристики абсолютно непрерывной случайной величины
1) Математическое ожидание
. (2.8)
2) Дисперсия
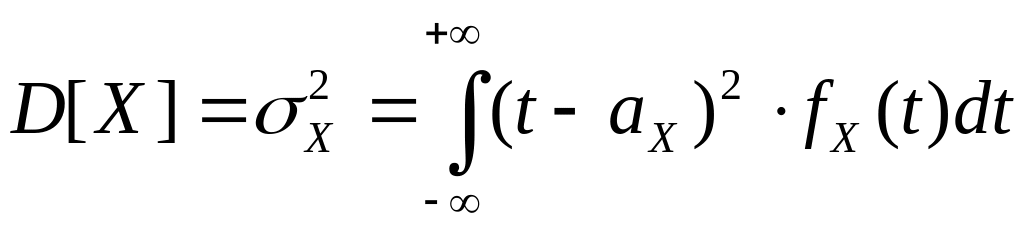. (2.9)
3)
Центральный момент порядка
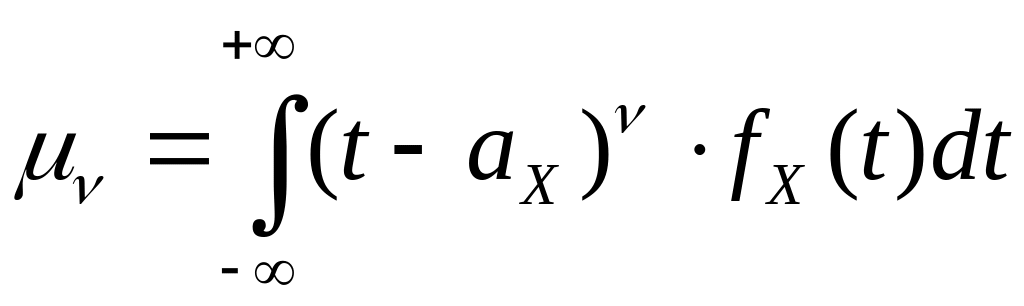. (2.10)
4)
Пусть двумерная СВ
имеет функцию плотности
:
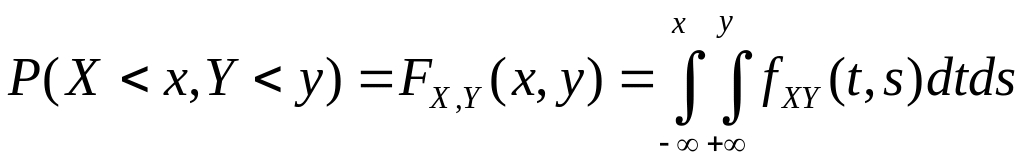. (2.11)
Тогда равенством
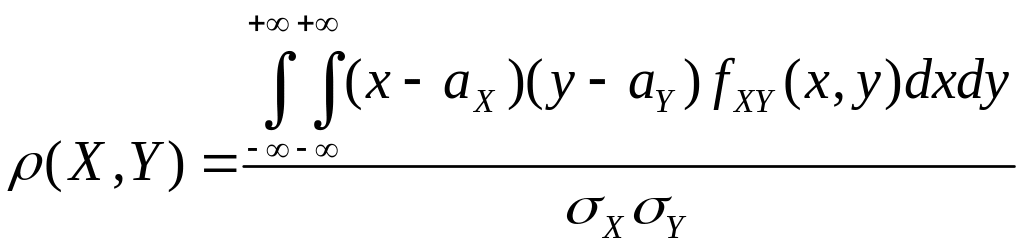(2.12)
определен коэффициент корреляции между случайными величинами и .
Коэффициент корреляции между двумя случайными величинами может принимать значения в отрезке [-1;1]:
. (2.13)
Если
, (2.14)
говорят об абсолютной положительной корреляции между величинами и (величины положительно зависят друг от друга в статистическом смысле).
Если
, (2.15)
имеет место абсолютная отрицательная корреляция между величинами и (величины отрицательно зависят друг от друга в статистическом смысле).
Статистические точечные оценки числовых характеристик
Обычно
точные значения числовых характеристик
не известны, приходится довольствоваться
их статистическими оценками, вычисляемыми
по выборке
наблюдений
за СВ
.
Число
называется объемом выборки. Будем
пользоваться следующими оценками.
1) Оценка математического ожидания – выборочное среднее
. (2.16)
2) Оценки дисперсии:
а)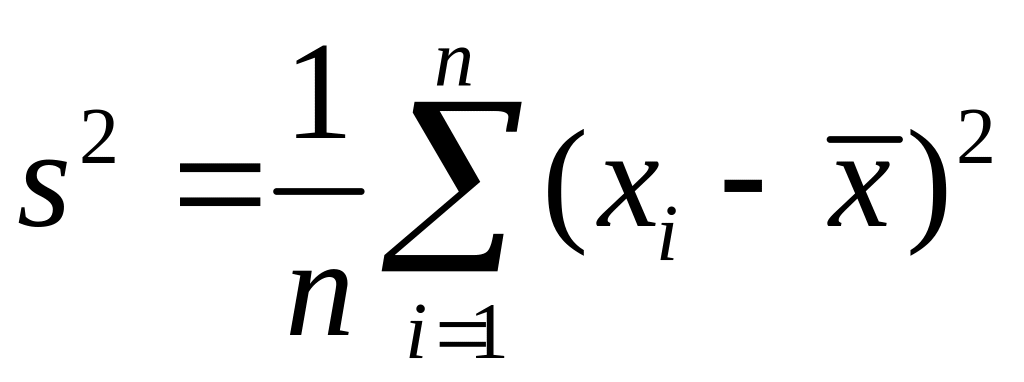 
, (2.17)
б)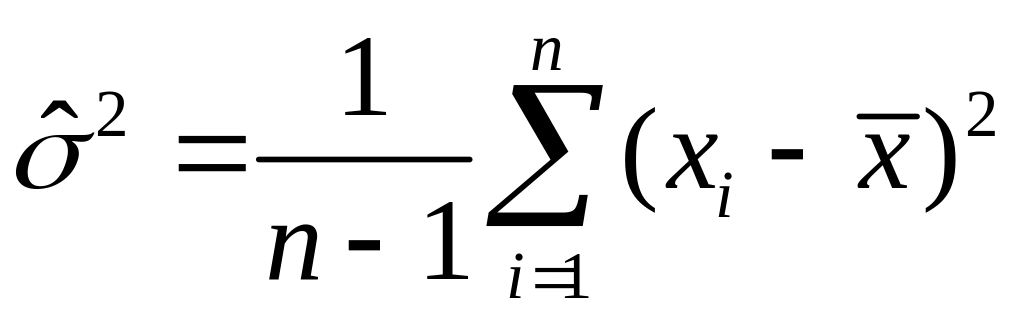 
, (2.18)
в)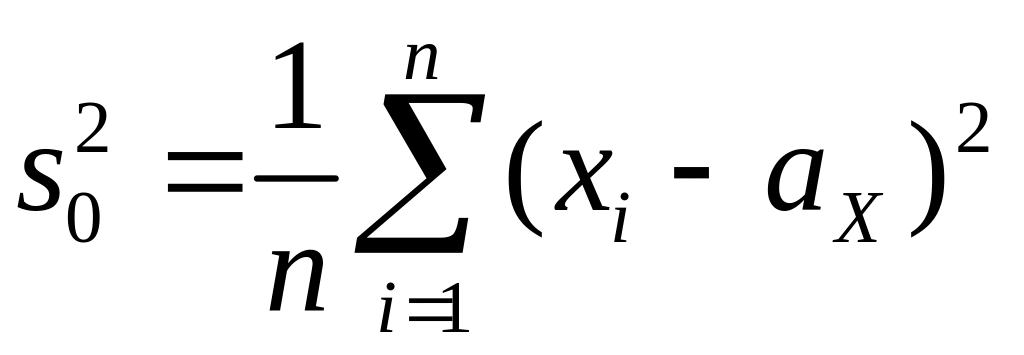 
. (2.19)
3) Оценка ковариации
. (2.20)
4) Оценка коэффициента корреляции
.
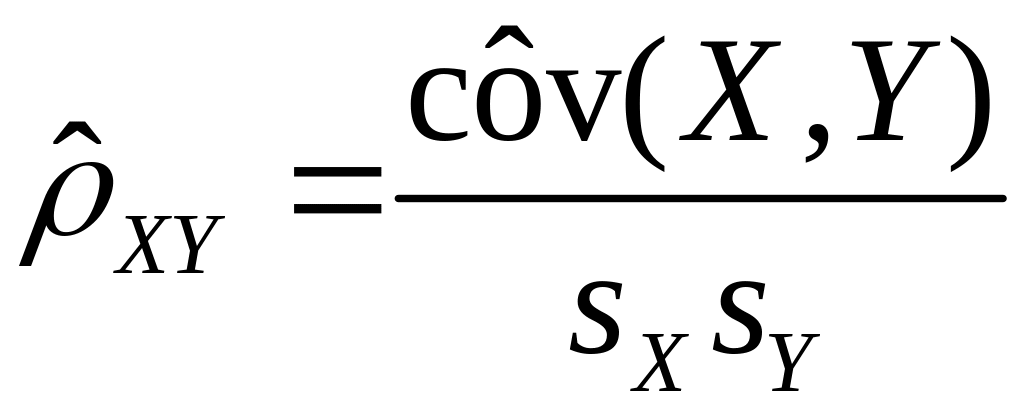(2.21)
Пусть
имеются наблюдения за случайными
величинами
с
одним и тем же объемом выборки n
для
каждой
из них. Кроме выборочных
коэффициентов
парной корреляции
для исследования частной
корреляции вводятся
коэффициенты
частной корреляции между
и
при исключении влияния остальных
переменных.
Для
каждой пары
выборочный
коэффициент частной корреляции
определяется равенством
где
-
алгебраическое дополнение элемента
-матрицы
.
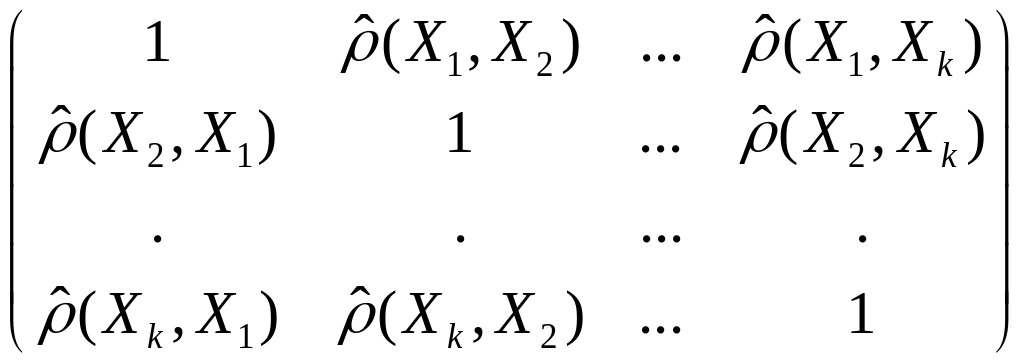Некоторые свойства статистических оценок (определения)
Пусть
– некоторый параметр (числовая
характеристика) СВ
.
Обозначим через
ее статистическую оценку, полученную
по выборке объема
.
Напомним определения некоторых свойств
точечных оценок.
1) Несмещенность:
. (2.22)
Оценки, не обладающие этим свойством, называются смещенными. Смещенность может возникать как следствие систематических ошибок при оценивании.
2) Состоятельность:
, (2.23)
или
, (2.24)
что
по определению означает:
. (2.25)
Таким образом, состоятельность – свойство сходимости по вероятности к оцениваемому параметру. В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки.
3) Эффективность.
Оценка
называется эффективной в фиксированном
классе
оценок, если
, (2.26)
т.е. эффективная оценка имеет минимальную дисперсию в заданном классе оценок.
Общий подход к построению интервальных статистических оценок параметров
Вычисленная
на основе выборки оценка
является лишь приближением к неизвестному
значению параметра
даже в том случае, когда эта оценка
состоятельная, несмещенная и эффективная.
Возникает вопрос: нельзя ли указать
такое ,
для которого с заранее заданной близкой
к единице вероятностью 1-
гарантировалось бы выполнение неравенства
: (2.27)
. (2.28)
Если
такое
существует, то интервал
называют
интервальной
оценкой
параметра
,
или доверительным
интервалом;
и
– нижней
и
верхней
доверительными границами
соответственно;
– ошибкой
оценки
,
– уровнем
значимости;
– надежностью
интервальной оценки,
или доверительной
вероятностью.
Выбор
доверительной вероятности определяется
конкретными условиями; обычно используются
значения
,
равные 0,90; 0,95; 0,99.
Возникают две задачи.
Задача 1. Задано , найти доверительную вероятность .
Задача 2. Задано или ( ), найти .
Первая задача решается стандартно:
. (2.29)
Для решения второй задачи используем следующий подход.
Строится
вспомогательная статистика
:
, (2.30)
распределение
которой (плотность вероятностей
)
не зависит от
и
(имеет место одно из стандартных
распределений, плотность которого не
зависит от
и
).
Далее из уравнения
(2.31)
находятся
и
.
При этом существенно используются
некоторые дополнительные предположения
и так называемые критические
значения стандартных распределений
(см. п. 2.3.2).
Таким образом, с вероятностью имеем
. (2.32)
Далее неравенство (2.32) решается относительно , при этом решение записывается в виде
. (2.33)
Таким образом, решение задачи построения интервальных оценок параметра сводится к нахождению так называемых критических значений стандартных распределений. Для этих значений составлены таблицы. Примеры построения конкретных оценок приводятся в параграфе 2.5.
Отметим, что если установить больший уровень доверия, то соответствующий доверительный интервал станет шире. Ширина доверительного интервала зависит от объема выборки, а также от разброса (изменчивости) данных: увеличение объема выборки делает оценку параметра более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки.