Интервальные оценки коэффициентов парной регрессии, полученные с помощью мнк

Интервальные оценки параметров и , определяющих детерминированную составляющую в модели линейной парной регрессии (3.1), могут быть получены на основе точечных оценок МНК и при дополнительном предположении о нормальном распределении случайного возмущения :

(3.60)

При этом линейность точечных оценок и относительно (а значит, и относительно ) приводит к нормальности распределения случайных величин и :

(3.61)

(3.62)

Отсюда сразу следует, что

(3.63)

и

. (3.64)

При заданном уровне значимости можно записать доверительные интервалы для и :

, (3.65)

. (3.66)

где и – двусторонние критические значения стандартного нормального распределения, соответствующие уровню значимости (см. п. 2.5). Таким образом, окончательно получаем

(3.67)

. (3.68)

Остается найти и .

Теоретические интервальные оценки

Рассмотрим сначала случай, когда значение в (3.60) известно. Найдем :

=

= . (3.69)

Здесь при вычислении дисперсии были использованы условия Гаусса – Маркова (3.22) – (3.24).

Вычисляя для (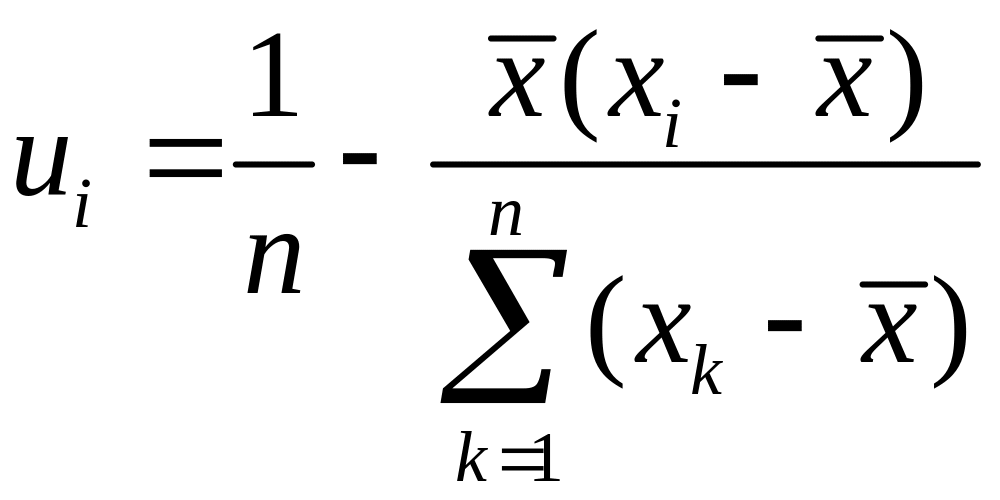см. 3.2.1), получаем

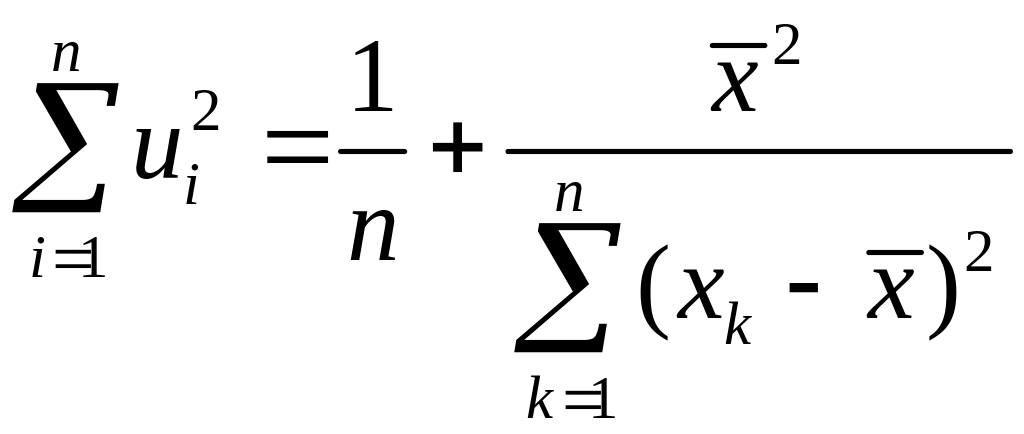. (3.70)

Аналогично для получаем

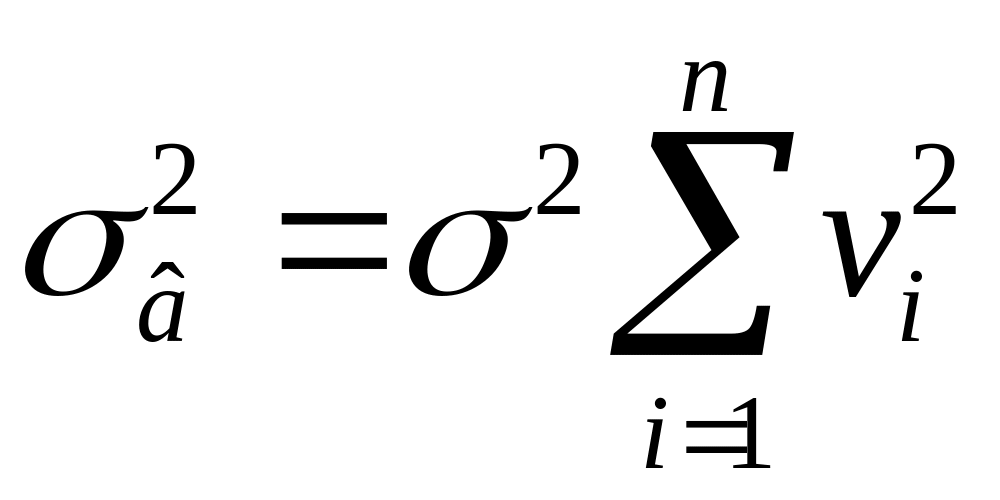, (3.71)

где

. (3.72)

Таким образом,

, (3.73)

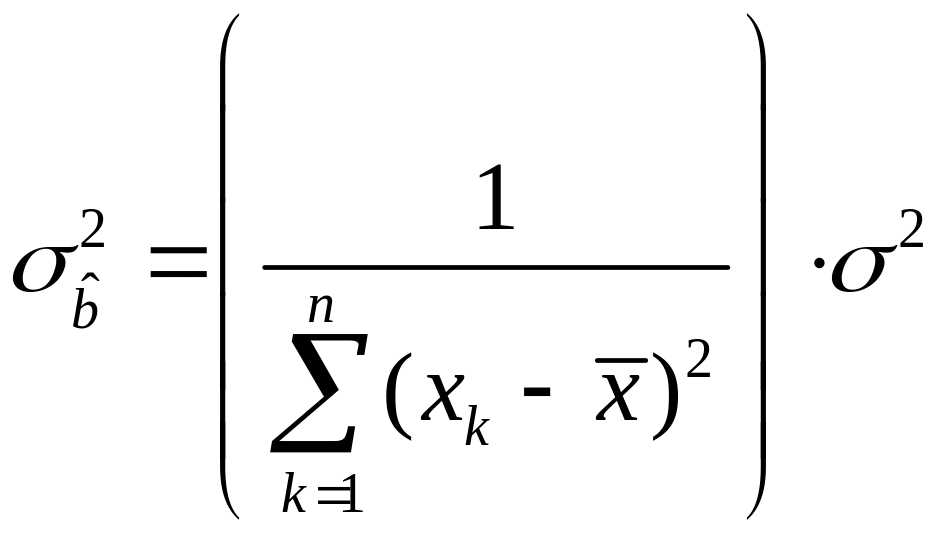, (3.74)

и с учетом (3.67) и (3.68) можно записать интервальные оценки для и в следующем виде:

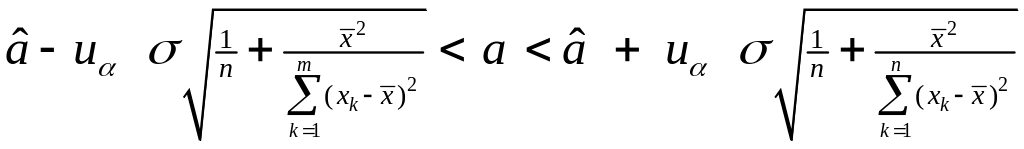, (3.75)

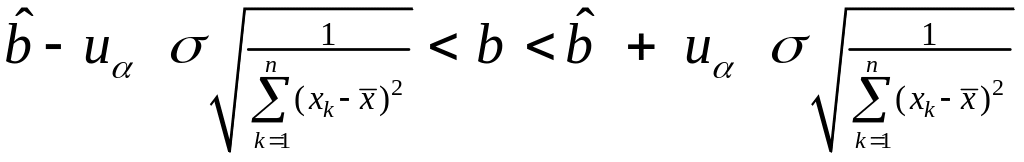. (3.76)

Подчеркнем, что этими оценками можно воспользоваться только при известном значении .

Практические интервальные оценки

В случае, когда значение неизвестно, приходится использовать его точечную оценку :

, (3.77)

которая может быть вычислена после нахождения выровненных значений . При этом

(3.78)

и

. (3.79)

Задавая уровень значимости , получаем, что с вероятностью

, (3.80)

, (3.81)

где – верхнее двустороннее критическое значение -распределения с степенями свободы.

Отсюда

(3.82)

. (3.83)

С учетом (3.73) и (3.74) имеем

, (3.84)

, (3.85)

и интервальные оценки, пригодные для практического применения, записываются в виде

, (3.86)

. (3.87)

Оценка качества модели линейной парной регрессии

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной. Проверка значимости уравнения регрессии производится в виде проверки соответствующей гипотезы при заданном уровне значимости.

Оценка значимости коэффициента линейной парной регрессии (t - тест)

Для оценки значимости (проверки гипотезы о значимости) коэффициента строится так называемая « -статистика»:

, (3.88)

которая имеет распределение Стьюдента с (n-2) степенями свободы. Далее задается уровень значимости и проводится сравнение с критическим значением .

В случае

(3.89)

принимается гипотеза о незначимости коэффициента , если же

, (3.90)

то принимается гипотеза о значимости , т. е. о значимом характере статистической зависимости объясняемой переменной от объясняющей переменной .