БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ "ВОЕНМЕХ"

им. Д. Ф. УСТИНОВА

Кафедра _И3_

КУРСОВАЯ работа

по учебной дисциплине __ Стохастические системы управления_____________________________

на тему _ Сокращение трудоемкости статистического моделирования _________________________

студента __________Абрамова Ильи Сергеевича _________________________________

Фамилия , Имя , Отчество студента

группы ______И381_____

Преподаватель

__Королёв С.Н.__ / ______________ /

Фамилия И.О. Подпись

"___" _________________ 2012 г.

САНКТ-ПЕТЕРБУРГ

2012 г.

Содержание

Введение………………………………………………………………………………..3

Основная часть……………………………………………………………………...4

1. Аналитическое решение………………………………………………………..4

2. Стандартная схема статистического моделирования………………………...6

3. Метод выделения главной части…………….…………………………………8

ЗАКЛЮЧЕНИЕ…………………………………………………………………………..11

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ……………………………………12

ПРИЛОЖЕНИЯ ………………………………………………………………………....13

1. Приложение 1 ………………………………………………………………....13

2. Приложение 2 ………………………………………………………………....16

Введение

Требуется определить математическое ожидание выходного сигнала X неустойчивого апериодического звена в заданный момент времени T. Модель звена:

, ,

содержит случайные параметры с равномерным законом распределения в заданных интервалах.

Допустимая абсолютная погрешность .

Задачу решить тремя способами:

• используя стандартную схему статистического моделирования;

• используя рациональную схему статистического моделирования с применением комбинированного метода сокращения трудоемкости;

• аналитически.

Результаты аналитического решения использовать для проверки результатов статистического моделирования и для обоснования построения рациональной схемы моделирования.

При использовании рациональной схемы статистического моделирования обеспечить снижение требуемого количества опытов по сравнению со стандартной схемой не менее чем в 10 раз.

Исходные данные (Вариант 1):

;

;

;

;

.

Основная часть

1 Аналитическое решение

В соответствии с заданием необходимо решить дифференциальное уравнение:

, , (1)

где g = G( t ),

X(0) = A.

Сначала найдем решение соответствующего однородного дифференциального уравнения:

Подставим полученное решение однородного дифференциального уравнения (1):

Найдем С₁ из условия X(0) = A:

В результате имеем:

Решение исходного дифференциального уравнения (1) имеет вид:

, (2)

Где где a – случайный параметр, распределенный по равномерному закону в интервале [0.5;1.1],

k - случайный параметр, распределенный по равномерному закону в интервале [0.6;1],

Для Т=1.2 с учетом статистической независимости k и a определим искомую характеристику:

Математическое ожидание выходного процесса определяется с учетом решения (2) [1]:

(3)

Дисперсия выходного процесса определяется с помощью уже найденного выше математического ожидания по формуле (3) [1]:

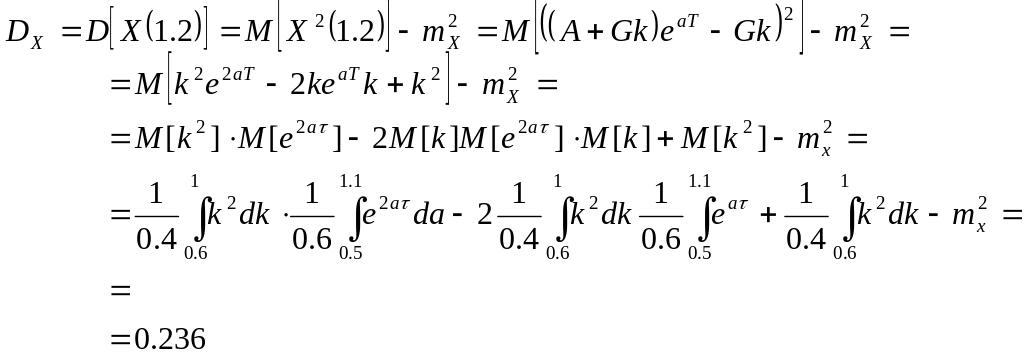(4)

Используя полученное аналитически значение дисперсии можно оценить требуемое количество опытов, которое необходимо было бы провести при решении методом статистического моделирования [1]:

, (5)

где параметр принят равным 3 (при доверительной вероятности Р_д=0,997.

Подставляя в формулу (5) значение, полученное по формуле (4), получим требуемое значение опытов :