
- •Основные источники погрешностей при разбивочных работах
- •Способы прямой и обратной угловых засечек
- •Погрешности исходных данных учитывают по формуле
- •Способ линейной засечки
- •Способ полярных координат
- •Р ис. 2.10. Схема разбивки способом проектного полигона
- •Способы створной и створно-линейной засечек
- •По формуле (2.55) погрешность центрирования имеет значение .
- •Способ прямоугольных координат
- •Способ бокового нивелирования
- •Погрешность отсчета по рейке подсчитывают по формуле
По формуле (2.55) погрешность центрирования имеет значение .
На основании формулы (2.58) совместное
влияние погрешностей визирования и
фокусирования составит
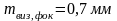 .
.
Общая
погрешность разбивки с учетом погрешностей
двух створов будет равна
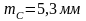 .
.
В приведенном расчете наиболее существенной оказалась погрешность исходных данных [6].
Створно-линейный способ позволяет определить проектное положение выносимой в натуру точки С (см. рис.2.11) путем отложения проектного расстояния d по створу АВ.
Разбивка этим способом точек сооружения или точек осей заключается в нахождении створа АВ. Измеряя отрезок АС=S на местности, в створе АВ находят искомую точку С. Точность способа будет обусловлена погрешностями задания створа, отложения проектного расстояния S и фиксации точки на местности
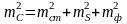 .
(2.59)
.
(2.59)
Причем погрешность створа определяется по формуле (2.53).
Широкое применение способ получил при выносе точек главных осей сооружений с пунктов строительной сетки. Створ задают при двух положениях круга теодолита. Длину линии откладывают лентой, рулеткой или с помощью дальномера. Для этого грубо намечают положение точки С в створе линии АВ. Затем точно измеряют расстояние, вводят поправки (за наклон, компарирование, температуру) и, определив разность между проектным расстоянием и измеренным, смещают точку по створу и закрепляют ее. Теодолит и визирное приспособление тщательно центрируют. Визирный луч должен проходить не ближе 1 м от поверхности земли и стен зданий.
Способ прямоугольных координат
Способ прямоугольных координат применяют в основном при наличии на площадке или в цехе промышленного предприятия строительной сетки, в системе координат которой задано положение всех главных точек и осей проекта.
Разбивку проектной точки С (рис. 2.12) производят по вычисленным значениям приращений ее координат х и у от ближайшего пункта сетки. Большее приращение (на рисунке — у) откладывают по створу пунктов сетки АВ. В полученной точке D устанавливают теодолит и строят от стороны сетки прямой угол. По перпендикуляру откладывают меньшее приращение х и закрепляют полученную точку С. Для контроля положение точки С можно определить от другого пункта строительной сетки.
Схема способа прямоугольных координат по существу сочетает в себе схему створно-линейного и полярного способов.
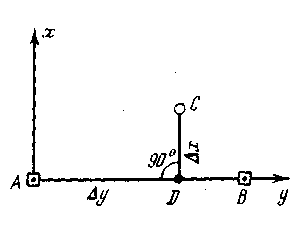
Средняя квадратическая погрешность в положении точки С, определенной способом прямоугольных координат, может быть выражена формулой
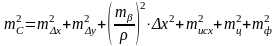 ,
(2.60)
,
(2.60)
где
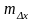 и
и
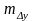 – погрешности отложения приращений
координат.
– погрешности отложения приращений
координат.
Если по перпендикуляру откладывается ордината, то в формуле (2.60) величина х заменяется на у.
Из формулы (2.60) следует, что большее приращение необходимо откладывать по створу стороны сетки, а меньшее — по перпендикуляру. В этом случае влияние погрешности построения прямого угла будет меньшим.
Влияние погрешностей в положении исходных пунктов при условии mA = mB = mAB выражается формулой
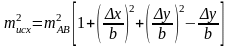 , (2.61)
, (2.61)
а погрешностей центрирования
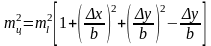 , (2.62)
, (2.62)
где b — длина стороны строительной сетки.
При разбивке точки С по перпендикуляру от стороны абсцисс в формулах (2.61) и (2.62) в последнем члене вместо у следует принимать х.
Рассчитаем для примера точность выноса в натуру проектной точки С, расположенной в середине квадрата строительной сетки со стороной 200 м. Примем относительную погрешность отложения расстояния равной 1:10000, m= 10", mAB= 10 мм, ml= 1 мм, mф= 1 мм.
Поскольку точка С расположена в середине квадрата строительной сетки, то х = у = 100 м. Для этого случая
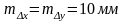 ;
; 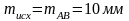 ;
;
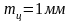 ;
; 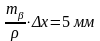 .
.
Подставив
эти данные в формулу (2.60), получим
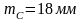 .
.
Погрешности центрирования и фиксации можно не учитывать, так как они малы по сравнению с величинами других погрешностей.
