4.9. Методы Монте-Карло

Методом Монте-Карло называется совокупность приемов, позволяющих получать решения математических или физических задач при помощи случайных многократных испытаний. На практике случайные испытания заменяются результатами вычислений, производимых над случайными числами.

Название «метод Монте-Карло» для методов, систематически использующих случайные величины, появилось в 1949 г. Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. Само название «Монте-Карло» происходит от названия города Монте-Карло княжества Монако, знаменитого своим игорным домом. Дело в том, что одним из простейших механических приборов для получения случайных величин является рулетка.

Методом Монте-Карло можно решать следующие задачи:

1. моделировать любой процесс, на протекание которого влияют случайные факторы;

2. для многих математических задач, не связанных с какими-либо случайностями, можно искусственно придумать вероятностную модель, позволяющую решать эти задачи.

Эффективное применение метода Монте-Карло стало возможным после появления ЭВМ, так как для получения достаточно точной оценки искомой величины требуется произвести вычисления для большого объема числовых данных. Это объясняется тем, что метод Монте-Карло использует различные предельные соотношения теории вероятностей – законы больших чисел и предельные теоремы.

Рассмотрим два простейших метода Монте-Карло вычисления кратных интегралов, которые достаточно легко реализуются на ЭВМ.

4.9.1. Простейший метод Монте-Карло

Рассмотрим вначале вычисление однократного интеграла. Пусть требуется вычислить интеграл вида:

, (4.47)

где функция задана на отрезке . Выберем произвольную плотность распределения случайной величины . Плотность определена на , причем и

.

Введем случайную величину , связанную со случайной величиной формулой

.

Математическое ожидание случайной величины равно

.

Таким образом, можно вычислить значение интеграла (4.47), вычислив математическое ожидание случайной величины . Для вычисления используются методы математической статистики. Пусть реализаций случайной величины . Тогда при достаточно большом значении получи4м

. (4.48)

При реализации метода Монте-Карло обычно в качестве используют равномерное распределение

(4.49)

Для того, чтобы получить реализации равномерно распределенной на случайной величины , достаточно иметь реализации случайной величины , равномерно распределенной на . Тогда

и, учитывая (4.49), получим

(4.50)

Аналогичный результат получится, если интеграл (4.47) путем замены переменной перевести в интервал . Тогда

,

где реализации случайной величины, равномерно распределенной на .

Рассмотрим вычисление многократного интеграла. Пусть требуется вычислить интеграл

, (4.51)

где область определяется неравенствами

(4.52)

При вычислении интеграла (4.51), область (4.52) с помощью линейной замены переменных

,

заключается в -мерный единичный куб. Тогда интеграл (4.51) запишется в виде

, (4.53)

где ─ якобиан преобразования,

,

область определяется неравенствами

(4.54)

Здесь

,

,

Интеграл (4.51) можно записать в виде

, (4.55)

где

. (4.56)

Метод Монте-Карло вычисления интеграла (4.56) заключается в следующем. Задается совокупность точек координаты которых являются независимыми случайными величинами, равномерно распределенными на интервале , и полагается

Тогда

.

Как правило, необходимо вычислить значение интеграла с заданной точностью , при этом понятно, что значения и взаимосвязаны: точность вычисления достигается при определенном значении . Рассмотрим подход к определению значения , который обеспечивает требуемую точность вычисления .

Пусть требуется вычислить интегралы:

(4.57)

или

, (4.58)

где область заключена в -мерный единичный куб.

На основании правила «трех сигм» можно записать, что

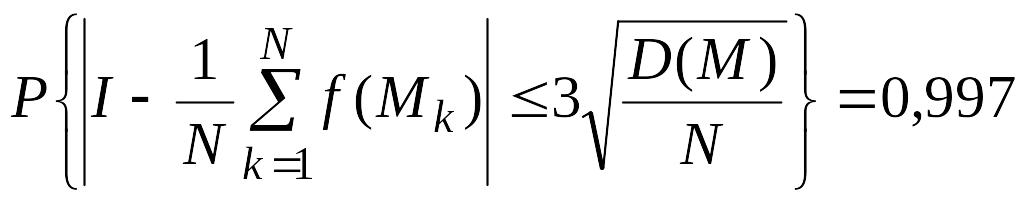, (4.49)

где точки, используемые для вычисления интеграла (4.57), координаты которых равномерно распределены на интервале , или точки, используемые для вычисления интеграла (4.58), координатами которых являются независимые равномерно распределенные на величины; , − значение интеграла и дисперсия, приближенно вычисляемые следующим образом

, (4.60)

. (4.61)

Формула (4.59) означает, что с вероятностью, близкой к единице, абсолютная погрешность вычисления интегралов (4.57) и (4.58) не превосходит величины . Отсюда следует, что необходимо задавать число таким образом, чтобы для требуемой точности было справедливо неравенство

. (4.62)

Для определения значения можно использовать итерационный алгоритм. Например, можно сначала задать число точек, равное , а затем увеличивать его по формуле пока не выполнится неравенство (4.62), где некоторое заданное целое число. При этом значения функций в суммах (4.60), (4.61) необходимо добавлять, не пересчитывая все заново.

Для уменьшения объема вычисления можно воспользоваться следующими рекуррентными формулами:

,

.