Проекции вектора
Если
известны величина вектора и его ориентация
относительно выбранной системы координат,
то легко найти проекции вектора. Пусть
ориентация вектора задана его углом 
относительно оси абсцисс.
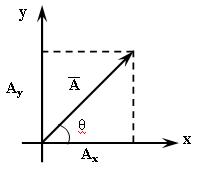
Рис. 3.11.
Тогда
и
.
Для
y-компоненты имеем:
.
Для любого вектора полезно ввести его собственный единичный вектор:
Из левого равенства следует, что любой вектор всегда равен его величине, умноженной на его собственный единичный вектор. Поскольку модуль любого числа, по определению, всегда положителен, то вектор и его собственный единичный вектор всегда сонаправлены. Правое равенство получается из теоремы Пифагора.
Действия над векторами, заданными своими координатами
Пусть
даны два вектора
и
.
Тогда:
а) равенство векторов равносильно равенству соответствующих координат:
;
б) коллинеарность векторов равносильна пропорциональности соответствующих координат:
;
в) линейные операции над векторами сводятся к линейным операциям над координатами:
,
,
;
г)
длина вектора вычисляется по формуле
;
д) направление вектора может быть задано с помощью направляющих косинусов (косинусов углов между вектором и положительными направлениями осей координат):
,
,
.
Направляющие
косинусы удовлетворяют соотношению
.
e) координаты орта a0 вектора a вычисляются по формуле:
.
Пример
3.1. Заданы
точки A(1; -2; 3), B(2; 0; -1). Найти вектор
.
Решение:
Пример 3.2. Сложение векторов, вычитание векторов, умножение на число.
Даны две точки на плоскости A(-1; 1 ), B(2; 5).
Тогда:
Пример
3.3. Даны A(-2;
3; 1), В(-1; 2; 0), С(0; 1; 1). Найти
.
Решение:
Пример
3.4. Известно,
что
.
Найти координаты точки D, если А(3; -4; -1),
В(-4; 4; 1), С(-3; -5; 4).
Решение:
Пусть
тогда
С другой стороны
Следовательно,
должно выполняться равенство
Отсюда
,
т.е. точка D имеет координаты D(2; 5; -4).
Пример 3.5. Даны две точки на плоскости A(-1; 1 ), B(2; 5). Необходимо: вычислить модуль вектора, направляющие косинусы и найти орт.
Решение:
Пример
3.6. Коллинеарны
ли векторы
и
,
где
и
?
Решение:
1.
Находим координаты векторов
и
,
пользуясь тем, что при сложении векторов
их координаты складываются, а при
умножении на число – координаты
умножаются на это число:
,
.
2.
Если координаты векторов
и
пропорциональны, т.е.
,
то векторы
и
коллинеарны. Если равенства не выполняются,
то векторы
и
неколлинеарны.
Так
как
,
то координаты пропорциональны.
Следовательно, векторы и коллинеарны.
Пример
3.7. При каком
значении m
векторы
и
перпендикулярны?
Решение:
Условие
ортогональности двух векторов
.
.
Следовательно,
.
Пример
3.8. Нормировать
вектор
.
Решение. Найдем длину вектора а:
Искомый единичный вектор имеет вид
.
Скалярное произведение векторов
Скалярным произведением ненулевых векторов и называется число, равное произведению их модулей на косинус угла между ними:
Под углом φ принимается угол между векторами, не превосходящий π. Если хотя бы один из векторов нулевой, то скалярное произведение полагают равным нулю.
Скалярное произведение обладает свойствами:
1)
(коммутативность),
2)
(ассоциативность
относительно умножения на число),
3)
(дистрибутивность
относительно сложения векторов).