Лекция 3 Элементы векторной алгебры. Основные понятия

Вектором называется направленный отрезок, у которого один конец называется началом вектора, другой конец называется концом вектора. Обозначаются векторы (полужирными) латинскими буквами или же помечаются стрелкой (чертой) сверху: AB, BA, a, b,

Вектор характеризуется длиной и направлением. 

Длиной (модулем) вектора называется число, обозначаемое символом (или же просто АВ) и равное длине отрезка АВ. 

Направление вектора задается указанием начала вектора и конца вектора. Две точки A и B определяют два вектора: вектор с началом в точке А и концом в точке В и вектор с началом в точке B и концом в точке A. Вектор называется вектором, противоположным вектору .

Нулевым вектором, обозначаемым символом , называется вектор, начало и конец которого совпадают. Длина нулевого вектора равна 0, направление считается не определенным.

Единичным вектором, или ортом, называется вектор, длина которого равна 1.

Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; обозначение коллинеарности: .

Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют равные модули. Все нулевые векторы считаются равными. При этом не имеет значения, в разных точках или в одной и той же точке векторы берут свое начало. Другими словами, если векторы при параллельном переносе совмещаются, то они равны.

Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

вектор равен вектору ;

вектор - противоположный вектору ;

вектор не равен , но коллинеарен и имеет с ним одинаковое направление;

если длина вектора в два раза больше длины вектора ( ), то ;

вектор не коллинеарен , не равен , но имеет с ним одинаковую длину;

вектор не равен

Рис. 3.1. Примеры векторов

Из определений следует, что различные векторы, полученные из некоторого заданного вектора путем параллельного переноса с сохранением длины и направления, считаются равными. Поэтому векторы, рассмотренные выше и изучаемые далее, называются свободными векторами. 

В математике и приложениях рассматриваются также скользящие векторы и связанные векторы.

Линейные операции над векторами Сложение и вычитание векторов

Сложение и вычитание векторов можно выполнить двумя способами: графически и алгебраически.

Сначала рассмотрим графический метод.

Сложение:

"Правило параллелограмма"

Складываемые векторы могут быть расположены произвольным образом друг относительно друга. Для графического сложения векторов сначала нужно совместить начала обоих векторов без изменения их направления. Это всегда можно сделать параллельным переносом одного из векторов или обоих векторов. На этом рис. 3.2. вектор параллельно перенесен таким образом, чтобы совместились начала обоих векторов. Теперь строится параллелограмм на векторах и как на образующих. Та диагональ параллелограмма, которая проходит через начало складываемых векторов, даст вектор суммы векторов . Векторы складываются по "правилу параллелограмма".

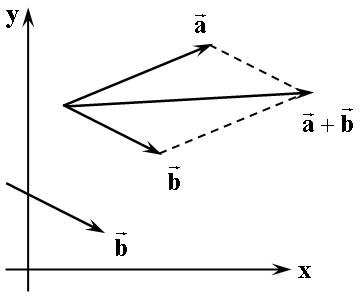
Рис. 3.2. Сложение векторов по правило параллелограмма

 

"Правило треугольника":

Можно поступить иначе. На рис. 3.3. вектор сначала параллельно смещен таким образом, чтобы его начало совместилось с концом вектора . Результирующий вектор соединяет начало вектора и конец вектора . Оба графических построения дают, очевидно, один и тот же результат.

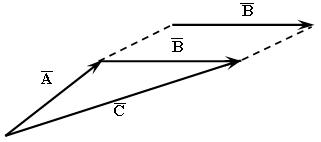
Рис. 3.3. Сложение векторов по правилу треугольника

Операция сложения векторов коммутативна (перестановочна): .

Выполняется также ассоциативный закон: . Графическое доказательство ассоциативности сложения векторов видно из рис. 3.4.: результирующий вектор можно получить либо сложив вначале , а затем , либо сначала , а затем .

Рис. 3.4. Свойство ассоциативности сложения векторов

Таким образом, операция сложения векторов обладает свойствами:

1) (коммутативность),

2) (ассоциативность),

3) (наличие нулевого элемента),

4) (наличие противоположного элемента), (символом обозначается вектор, противоположный вектору ).

Вычитание:

Вернемся к рис. 3.2: вторая диагональ параллелограмма дает величину вектора разности - векторов и . При этом направление вектора разности векторов и определяется от конца вектора к концу вектора .