Лекция 1 Определители. Свойства определителей

Определителем второго порядка называется число, обозначаемое символом и определяемое равенством .

Определитель также носит название детерминант (det).

Например, вычислить определитель .

Числа, составляющие определитель называются его элементами: , где i и j – номер строки и столбца, на пересечении которых находится элемент.

Определитель второго порядка имеет две строки и два столбца.

Определитель третьего порядка называется число, обозначаемое символом и определяемое равенством

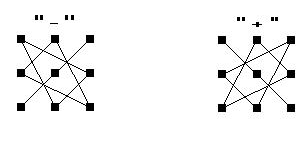
– главная диагональ;

– побочная диагональ.

Например,

Основные свойства определителей:

1. Величина определителя не изменится от замены строк столбцами (транспонировании). Это свойство определяет равноправность строк и столбцов.

2. Величина определителя изменит знак на обратный при перестановке местами двух любых строк или столбцов.

3. Определитель равен нулю, если две его строки или два его столбца пропорциональны.

4. Общий множитель строки (столбца) можно вынести за знак определителя, т.е.

.

5. Правило сложения определителей

Следствие: величина определителя не изменится, если к элементам одной строки (столбца) прибавить соответственные элементы другой строки (столбца), умноженные на произвольное число.

Например, .

Минор. Алгебраическое дополнение

Минором элемента называется определитель, полученный из данного путем вычеркивания i строки j столбца, т.е. той строки и того столбца, на пересечении которых стоит элемент . Минор есть определитель порядка на единицу ниже исходного.

Например, в определителе, Минором к элементу 4 является

Алгебраическое дополнение есть минор , умноженный на , т.е. .

В приведенном примере

В данном случае Минор и алгебраическое дополнение к элементу 4 совпали.

Продолжим изложение свойств определителей.

6. Величина определителя равна сумме произведений элементов любой строки (столбца) на соответствующее алгебраическое дополнение этих элементов.

Например, ; правая часть равенства называется разложением определителя по элементам первой строки.

7. Сумма произведений элементов строки на алгебраические дополнения к элементам другой строки равна нулю.

Например,

Перечисленные свойства определителей справедливы для определителей любого порядка.

Пример 1.1. Вычислить определитель двумя способами.

Решение. Первый способ.

Второй способ. Разложим определитель по элементам второго столбца.

Ответ: -2

Матрицы. Основные операции над матрицами

Матрицей размера называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

.

Элемент матрицы , стоящий на пересечении i-ой строки и j-ого столбца обозначают Приведем примеры матриц.

, , , .

Разновидности матриц.

1. Матрица называется прямоугольной, если .

2. Матрица называется квадратной, если .

3. Матрица называется матрицей - строкой, если .

4. Матрица называется матрицей - столбцом, если .

Например, 1) – прямоугольная матрица размерности 2*3 (два на три);

2) – квадратная матрица;

3) – матрица строка;

4) – матрица столбец.

Квадратная матрица называется треугольной, если все элементы матриц, расположенные выше или ниже главной диагонали равны нулю.

Например, или .

Квадратная матрица называется диагональной, если все ее элементы, кроме элементов главной диагонали, равны нулю.

Например, .

Квадратная матрица называется единичной, если элементы диагональной матрицы, стоящие на главной диагонали равны единице.

.