5.2. Квадратичная, кубическая, геометрическая, гармоническая средние

Средняя квадратичная величина – это такая средняя, которая сохраняет неизменной сумму квадратов значений признака при замене индивидуальных значений на средние:

(4)

(5)

Применяется, например, в вариационном анализе (тема 5, п. 5.5).

Средняя кубическая величина – это такая средняя, которая сохраняет неизменной сумму кубов значений признака при замене индивидуальных значений на средние:

(6)

(7)

Средняя геометрическая величина – это такая средняя, которая сохраняет неизменным произведение значений признака при замене индивидуальных значений на средние. Рассчитывается в тех случаях, когда индивидуальные и общее значения связаны как сомножители и произведение:

(8)

Пример. Предположим, что объем продаж на предприятии вырос в 2003 году в 3 раза, а в 2004 году в 2 раза. За два года показатель вырос соответственно в 6 раз.

Очевидно, что индивидуальные значения признака (2 и 3 раза) связаны с общим (6 раз), как сомножители и произведения. Следовательно, среднюю следует рассчитывать как геометрическую:

То есть, можно сказать, что в среднем каждый год значение показателя увеличивалось в 2,45 раза.

Проверим. Действительно, если бы в первый год увеличение произошло в 2,45 и во второй – в 2,45, то в целом за два года показатель увеличился бы в 6 раз:

Если бы в данном случае была определена арифметическая средняя (2+3)/2 = = 2,50, то проверочный расчет показал бы ошибку:

Таким образом, принципиально важно уметь определить, какую именно среднюю корректно рассчитывать в конкретной задаче.

Средняя гармоническая величина – это такая средняя, которая сохраняет неизменной сумму значений, обратных значениям признака при замене индивидуальных значений на средние:

(9)

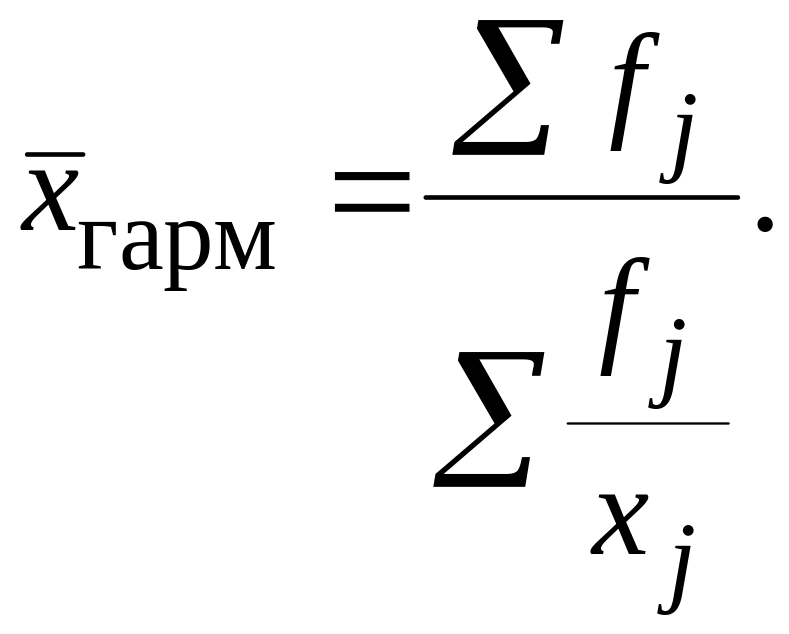(10)

Рассчитывается, например, при определении средней из коэффициентов оборачиваемости оборотных средств.

Правило мажорантности средних. Для средних величин, рассчитанных по одному и тому же набору исходных данных выполняется соотношение

(11)

Это соотношение можно использовать при проверке расчетов в статистическом анализе, в частности, в вариационном анализе.

5.3. Многомерная средняя величина

Многомерная средняя величина – это обобщенная характеристика некоторого явления, построенная на основе сведения в единый показатель частных его характеристик. Используется для ранжирования объектов по возрастанию или убыванию какого-либо сложного явления (свойства).

Расчетные формулы для случая простой и взвешенной средней:

(12)

(13)

Примечание: данные расчетные формулы применимы только для случаев, в которых явление (свойство) характеризуется набором прямых показателей (см. тему 4, п. 4.2).

Пример. Пусть необходимо проранжировать магазины по уровню обслуживания покупателей (табл. 5.2).

Для того чтобы ранжировать магазины по возрастанию (или убыванию) уровня обслуживания необходимо рассчитать для каждого из них значение сводного показателя, который объединял бы в себе все существенные для оценки стороны их деятельности. Представленные в таблице показатели невозможно просто суммировать по каждому магазину, так как это показатели с различными единицами измерения – нельзя складывать часы с количеством жалоб или оценочными баллами. Таким сводным показателем может быть многомерная средняя величина, при расчете которой каждое индивидуальное значение признака нормируется (соотносится со средним по всей совокупности значением признака), и, таким образом, суммируются не сами значения признаков и их отношения к средней, т. е. безразмерные величины. Все используемые показатели являются прямыми по отношению к оцениваемому явлению – уровню обслуживания (чем выше значение показателя, тем выше уровень обслуживания). Веса вводятся в том случае, если необходимо учесть различную значимость составляющих обобщенную оценку факторов. Например, если определено или задано, что оценка качества работы персонала покупателями в 2 раза важнее чем число зарегистрированных жалоб, то весовой коэффициент (или вес) первого признака должен быть в 2 раза больше чем у второго. Обычно веса устанавливают в долях единицы, так чтобы сумма весов была равна 1, либо в процентах, так чтобы сумма весов была равна 100 %, но возможны и другие варианты.

Таблица 5.2