4.5.4. Сложная функция

Пусть функция z = φ (х) с множеством значений Z , определена на множестве Х и на множестве Z также определена функция у = f (z) с множеством значений Y , тогда функция у = f[φ (х)] называется сложной функцией от аргумента х, а переменная z называется промежуточной переменной сложной функции.

Например, сложная функция, определённая на множестве (-∞, 0) (-1, +∞) , так как у = f (z) = , z = φ (х) = .

4.5.5. Основные элементарные функции

Элементарные функции, изучаемые в школьном курсе математики, являются математическими моделями простейших механических, физических и др. явлений. Например, тригонометрические функции и хорошо описывают колебательные движения.

Основными элементарными функциями называют следующие функции.

1. Степенная функция , где α – действительное число.

2. Показательная функция .

3. Логарифмическая функция .

4. Тригонометрические функции: , , , .

5. Обратные тригонометрические функции: , , , .

6. Алгебраической функцией называется функция в которой над аргументом производится конечное число алгебраических операций (сложение, вычитание, умножение, деление, возведении в степень, извлечение корня, решение алгебраического уравнения).

Всякая неалгебраическая функция называется трансцендентной.

Простейшие типы алгебраических функций:

1. Целая функция (многочлен или полином) -

,

над аргументом х производятся действия сложения, вычитания, умножения и возведения в целую положительную степень..

2. Дробная (рациональная) функция

,

над аргументом х производится ещё действие деления.

3. Иррациональная функция: над аргументом х производится ещё действие извлечения корня. Например, .

4.5.6. Предел функции

Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)

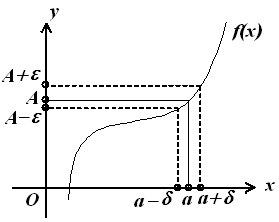
Рис. 4.1

Определение. Число А называется пределом функции f(x) при х  а, если для любого  > 0 существует такое число δ > 0, что для всех х таких, что

0 < x - a < δ

верно неравенство f(x) - A< .

То же определение может быть записано в другом виде:

если а - δ < x < a + δ, x  a, то верно неравенство А -  < f(x) < A + .

Запись предела функции в точке: .

При определении предела функции предполагается, что х стремится к а произвольным образом: оставаясь меньше, чем а (слева от а), большим, чем а (справа от а), либо колеблется около точки а. Поэтому имеет смысл ввести понятия односторонних пределов.

Определение. Если f(x)  A₁ при х  а только при x < a, то - называется пределом функции f(x) в точке х = а слева, а если f(x)  A₂ при х  а только при x > a, то называется пределом функции f(x) в точке х = а справа ( рис. 4.2).

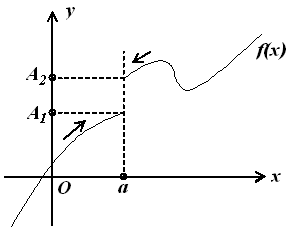
Рис. 4.2.

Таким образом, условие существования предела функции сводится к тому, что при х  а для функции f(x) должны существовать левосторонний и правосторонний пределы и при этом они должны быть равными.