Министерство экономического развития и торговли Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

САНКТ-ПЕТЕРБУРГСКИЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Кафедра высшей математики

Оптимизационные задачи в экономике и алгоритмы решения некоторых задач линейного программирования Учебное пособие по курсу «математика»

САНКТ-ПЕТЕРБУРГ 2004

Авторы: И.В.Вагурина, А.Е. Иванов, И.В.Медведева, Е.А.Смирнова, С.В.Ульянов

Рассмотрены проблемы математической формализации экономических оптимизационных задач, алгоритмы их геометрического и аналитического решения.

Учебное пособие предназначено для студентов заочной и заочной сокращенной форм обучения специальностей 06.08.00, «Экономика и управление на предприятии торговли и общественного питания», 06.05.00 «Бухгалтерский учет, анализ и аудит», 35.11.00 «Товароведение и экспертиза товаров», изучающих раздел «Математическое программирование» дисциплины «Математика».

Рецензент; доктор физ.-мат.наук, проф. А.Ю.Вальков (ИВЭСЭП)

§1. Математическая формализация оптимизационной проблемы

Искусство управления может рассматриваться как искусство выбора наилучшей с точки зрения управляющего альтернативы среди всех реализуемых альтернатив. В математике процесс выбора наилучшей альтернативы принято называть оптимизацией. Как известно, одним из основных отличий науки от искусства является возможность алгоритмизации. Воспользуемся простейшей задачей производственного планирования [Mathur, с. 159] и сформулируем алгоритм постановки оптимизационной задачи.

 1 Математическая формализация оптимизационной проблемы

Ф ирма Creative Coffees производит и продает два сорта кофе: Regular и Decaf. На текущий месяц запас кофейных зерен на складе фирмы составляет 200 тонн, а суммарное время жарки зерен ограничено 300 часами. Каждая тонна кофе Regular производится из одной тонны зерен, обжариваемых в течение одного часа, и приносит производителю прибыль в размере $3000. Каждая тонна кофе Decaf также производится из одной тонны зерен, но обжариваемых в течение двух часов, и приносит фирме прибыль в размере $5000. Представим условия задачи в табличной форме:

Таблица 1

	Regular (т)	Decaf (т)	Запас сырья
Зерна (т)	1	1	200
Время жарки (ч)	1	2	300
Прибыль от продажи ($1000/т)	3	5

Определим план выпуска кофе, при котором прибыль фирмы за текущий месяц будет максимальна.

 1. Переменные, подлежащие определению в результате решения задачи, называются оптимизируемыми. Вектор оптимизируемых переменных называется альтернативой или планом.

• Укажем переменные, подлежащие определению в результате решения задачи, и введем понятие плана.

В результате решения задачи производителю (продавцу) необходимо определить, какое количество каждого из сортов кофе следует выпустить. Введем следующие обозначения:

x₁ – количество кофе Regular, которое следует произвести в текущем месяце,

x₂ – количество кофе Decaf, которое следует произвести в текущем месяце,

и назовем вектор x=(x₁, x₂) планом выпуска.

Как правило, в каждой проблемной ситуации существует ряд ограничений, не позволяющих реализовать на практике те или иные альтернативы.

 2. Планы, которые могут быть практически реализованы, называются допустимыми. Множество допустимых планов называется допустимым множеством.

Допустимость альтернативы определяется, в основном, ограниченностью ресурсов, находя­щихся в распоря­жении предпринимателя. Отметим ряд типичных ограничений, которые определяют мно­жество допустимых альтер­натив в процессе принятия управленческих решений.

Производственные ограничения – это ограничения, связанные с возможностью выпустить и реализовать ограниченное количество продукции (оказать ограниченный объем услуг), располагая ограни­ченным количеством ресурсов (денежных средств, сырья, производственных помещений и оборудования, рабо­чего времени и квалификации персонала).

Рыночные (сбытовые) ограничения – это ограничения, связанные с возможностью реализо­вать ограниченное количество продукции в рамках избранной ценовой стратегии, а также с необходимостью выполнения заключенных контрактов.

Временные ограничения – это ограничения на время, отпущенное на решение пробле­мы.

Логические ограничения – это ограничения, связанные с природой оптимизируемых перемен­ных (например, неотрицательность цен, объемов затрат ресурсов и потребления товаров).

Внешние ограничения – это социальные, правовые, этические ограничения, порожденные воздействием общества на бизнес.

• Составим уравнения и неравенства, определяющие множество допустимых планов.

Допустимость плана в задачах производственного планирования определяется, прежде всего, тем, хватит ли имеющихся в наличии ресурсов на его реализацию. Выпуск x₁ тонн кофе Regular требует x₁ тонн кофейных зерен и x₁ часов их жарки, а выпуск x₂ тонн кофе Decaf требует x₂ тонн кофейных зерен и 2x₂ часов их жарки. Таким образом, план x=(x₁, x₂) допустим, если

(1)

Производственные ограничения дополняются логическими ограничениями, связанными с природой введенных в рассмотрение переменных. В данном случае объемы выпуска товаров не могут быть отрицательными: x0. (2)

Рассмотрим геометрическую интерпретацию понятий: план, допустимый план, множество допустимых планов. Введем в рассмотрение декартову прямоугольную систему координат с осями, соответствующими оптимизируемым переменным, и, учитывая неравенство (2), изобразим ее первый квадрант (рис. 1). Любая точка в нем – план выпуска x=(x₁, x₂), причем план допустим, если его координаты удовлетворяют соотношениям (1), и не допустим – в противном случае.

Изобразим все планы, на которые хватит зерен кофе: x₁+x₂200. С этой целью построим отрезок прямой x₁+x₂=200. На этом отрезке лежат планы выпуска, полностью исчерпывающие запас зерен, ниже – планы, на которые зерен хватит с избытком, выше – не допустимые планы.

Изобразим все планы, на реализацию которых хватит времени: x₁+2x₂300. С этой целью построим отрезок прямой x₁+2x₂=300. На этом отрезке лежат планы выпуска, полностью исчерпывающие запас времени, ниже – планы, на которые времени хватит с избытком, выше – не допустимые планы.

Т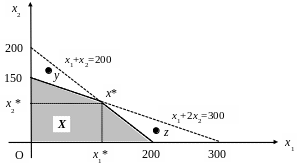 аким образом, множество допустимых планов – есть затененная область X на рис. 1 (множество планов, на реализацию которых хватит и первого, и второго ресурса):

Рис. 1 Допустимое множество в проблеме производственного планирования

 Почему невозможно реализовать план y, план z (рис. 1)?

Возникает вопрос: какой из допустимых планов является лучшим для про­изводителя?

 3. Функция, сопоставляющая альтернативам действительные числа, называется целевой (критериальной), если большее (меньшее) ее значение указывает на строго более предпочтительную альтернативу, а одинаковые значения – на равноценные альтернативы.

• Построим целевую (критериальную) функцию

В рассматриваемой задаче из двух допустимых планов лучшим является тот, который принесет фирме большую прибыль. При реализации плана x=(x₁, x₂) прибыль составит

(x)=3x₁+5x₂

тысяч денежных единиц.

Как отмечалось выше, в процессе планирования производитель ищет такой реализуемый план выпуска товара, который принесет ему наибольшую прибыль. Приведем общую математическую постановку такого рода оптимизационных задач.

Предположим, имеется n оптимизируемых переменных, и, соответственно, план x является n–мерным вектором. Обозначим допустимое множество через X, целевую функцию через F.

 4. Глобальным максимумом (минимумом) функции F(x) на множестве X называется та­кой допустимый вектор х*X, что

F(x*) F(x) (F(x*) F(x)) xX.

(3)

 Максимумы и минимумы функции принято называть ее экстремумами.

 5. Задача нахождения глобального максимума (минимума) функции F(x) на множестве X называется задачей математического программирования (ЗМП) и записывается в виде

F(x) max, xX (F (x) min, xX).

(4)

Решение задачи (4) обозначается

x* = argmax F(x), xX, (x* = argmin F(x), xX),

и называется оптимальным планом. Число F(x*) называется значением задачи (4) и обозначается max F(x) (min F(x)).

 6. Решить ЗМП – значит найти все ее решения или доказать, что их не существует.

• Выпишем получившуюся математическую модель оптимизационной задачи или задачу математического программирования:

(x)=3x1+5x2  max,

(5)

Таким образом, для математической формализации проблемы производственного планирования фирмы Creative Coffees мы воспользовались следующим алгоритмом.

Алгоритм математической формализации оптимизационной проблемы

• Указать переменные, подлежащие определению в результате решения задачи, ввести понятие плана

• Составить уравнения и неравенства, определяющие множество допустимых планов

• Построить целевую (критериальную) функцию

• Выписать получившуюся задачу математического программирования

 7. Задача математического программирования, целевая функция которой является линейной, а допустимое множество задано системой линейных уравнений и неравенств, называется задачей линейного программирования (ЗЛП).

 8. ЗЛП называется стандартной задачей линейного программирования, если

все ограничения выражены линейными неравенствами одинакового направления (как правило, ),

все оптимизируемые переменные предполагаются неотрицательными.

Таким образом, задача (5) – стандартная задача линейного программирования. Если ввести обозначения

ее можно записать в виде

(x)=сx  max, Axb, x0.

 9. ЗЛП называется канонической задачей линейного программирования, если

все ограничения выражены линейными равенствами,

все оптимизируемые переменные предполагаются неотрицательными.

Для приведения стандартной задачи линейного программирования к канонической следует

• все неравенства системы ограничений заменить равенствами, введя в левой части каждого неравенства дополнительную переменную.

 1. Перейдите от стандартной ЗЛП (5) к канонической.

 2. К аждый галлон молока, фунт сыра и яблок обеспечивает организм определенным коли­чеством миллиграмм про­теина и витаминов A, B, C в соответствии с данными приведенной ниже таблицы. Наряду с этими данными, таблица содержит ин­формацию о минимальных ежедневных потребностях организма в вышеупомянутых веществах, пред­ставленную Де­партаментом сельского хозяйства США. Кроме того, в таблицу включены данные о минимальном количестве каждого из продуктов, которое должно войти в меню, и цены продуктов.

Таблица 1

	Молоко (мг/галлон)	Сыр (мг/фунт)	Яблоки (мг/фунт)	Минимальные потребности организма (мг)
Протеины	40	30	10	80
Витамин A	5	50	30	60
Витамин B	20	30	40	50
Витамин С	30	50	60	30
Минимальное количество в диете	0,5 гал.	0,5 фунта	0,5 фунта
Цена ($)	2,15	2,25	1,25

Постройте математическую модель оптимизационной проблемы, предполагая, что из двух диет, обеспечивающих организм необходимым количеством питательных веществ, лучшей является более дешевая.