6.2.2 Решение прямой краевой задачи теплопроводности, лежащей в основе метода регулярного режима первого рода

Сначала получим (методом разделения переменных) решение прямой краевой задачи теплопроводности (6.12) – (6.15).

6.2.2.1 Представление решения краевой задачи теплопроводности в виде произведения двух функций

Решение задачи (6.12) – (6.15) будем искать в виде

(6.12а)

Тогда

После подстановки этих соотношений в уравнение (6.12) получаем

.

Если это уравнение поделить на то получим равенство

. (6.17)

Левая часть равенства (6.17) зависит от безразмерной временной координаты – числа Фурье , а правая часть – от безразмерной пространственной координаты , т.е. мы имеем равенство двух функций, каждая из которых имеет свою независимую переменную.

Возникает вопрос: "При каком условии две функции, зависящие от разных переменных величин (аргументов) и , могут быть равны между собой?". Возможен только один ответ на этот вопрос: "Две функции, стоящие в левой и правой сторонах равенства (6.17), зависящие от разных аргументов и , могут быть равны только при условии, что каждая из них равна константе". Эта константа в равенстве (6.17) записана в виде .

С учетом сказанного выше исходная прямая краевая задача теплопроводности (6.12) – (6.15) разделяется на две задачи.

Первая задача определяет зависимость искомого решения (6.12а) от безразмерного времени и записывается в виде обыкновенного дифференциального уравнения

(6.18)

общее решение которого имеет вид

. (6.18а)

Примечание. Если бы правую и левую части равенства (6.17) приравняли положительному числу ², то уравнение (6.18) приобрело бы вид и имело бы неустойчивое решение

,

которое быстро стремится к бесконечности по мере роста безразмерного времени Нас интересует устойчивое решение исходной прямой краевой задачи теплопроводности (6.12) – (6.15). Именно поэтому левую и правую части (6.17) мы приравняли отрицательной константе, что записано в (6.17) в виде . Любая величина, возведенная в квадрат, дает положительное число . Тогда величина всегда является отрицательной, что позволяет в дальнейшем получить устойчивое (не обращающееся в бесконечность) решение (6.18а) уравнения (6.18).

Получившееся решение (6.18а) будет использовано нами в дальнейшем.

Вторая задача, получающаяся в результате применения метода разделения переменных, имеет вид

(6.19)

(6.20)

(6.21)

Задача (6.19) – (6.21) представляет собой хорошо изученную в математике краевую задачу Штурма-Лиувилля [19].

6.2.2.2 Свойства решений краевой задачи Штурма-Лиувилля

Решения краевой задачи Штурма-Лиувилля (6.19) – (6.21) существуют при вполне определенных значениях . Эти значения и соответствующие им решения называются собственными значениями и собственными функциями краевой задачи Штурма-Лиувилля и обладают следующими свойствами [19]:

1. существует бесконечное (счетное) множество собственных значений 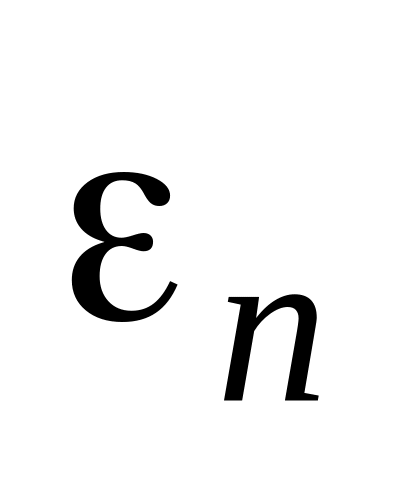и соответствующих им собственных функций краевой задачи (6.19) – (6.21); индекс может принимать значения ;

2. если является собственной функцией краевой задачи (6.19) – (6.21) и K = const, то тоже собственная функция краевой задачи Штурма-Лиувилля (6.19) – (6.21);

3. собственные функции и ортогональны на отрезке с весом , т.е.

(6.22)

где так называемая норма функции ; если ввести функции , то очевидно, что в силу сформулированного выше второго свойства краевой задачи (6.19) – (6.21), тоже является собственной функцией, причем

;

называют ортонормированными собственными функциями краевой задачи Штурма-Лиувилля (6.19) – (6.20);

4. всякая непрерывная на отрезке функция разлагается в ряд Фурье по собственным функциям краевой задачи Штурма-Лиувилля, т.е.

, (6.23)

где коэффициент разложения функции в ряд Фурье (6.23).

Перечисленные выше свойства собственных функций краевой задачи Штурма-Лиувилля позволяют легко находить коэффициенты разложения функции в ряд Фурье.

Рассмотрим порядок получения значений коэффициентов Умножим левую и правую части равенства (6.23) на , а затем, после замены аргумента на переменную интегрирования и интегрирования в пределах от 0 до 1, получим

.

Принимая во внимание, что в силу свойства ортогональности (6.22) в правой части последнего равенства все интегралы (при ) равны нулю, кроме одного , получаем

,

откуда следует (после замены обозначения индекса на обозначе- ние п) формула для вычисления коэффициентов разложения в ряд Фурье (6.23)

. (6.23а)