6.3.2 Метод регулярного режима второго рода для двухслойной системы

6.3.2.1 Физическая модель метода и устройства для его осуществления

Схема используемой в рассматриваемом случае двухслойной системы [3], включающей в себя исследуемую теплоизоляционную пластину 1 толщиной R и металлическое ядро 2, толщиной , представлена на рис. 6.8.

Рис. 6.8 Графическая иллюстрация осуществления относительного метода регулярного режима второго рода [3]:

а – схема используемой двухслойной системы;

б – характер изменения температур в процессе эксперимента

Относительно тонкая теплоизоляционная пластина 1 толщиной R находится в идеальном тепловом контакте с металлической (медной) пластиной 2, имеющей толщину .

На левую грань пластины 1 (при ) действует постоянный тепловой поток Правая грань пластины 2 адиабатизирована ( ), что позволяет (благодаря высокой теплопроводности меди) получить практически равномерное температурное поле при в пластине 2 (см. рис. 6.8).

6.3.2.2 Порядок осуществления измерительных операций

При практическом использовании рассматриваемого относительного варианта метода регулярного режима второго рода измерительные операции осуществляют в следующем порядке [3].

1. Из исследуемого материала изготавливают плоский образец с относительно небольшой толщиной R квадратной формы площадью 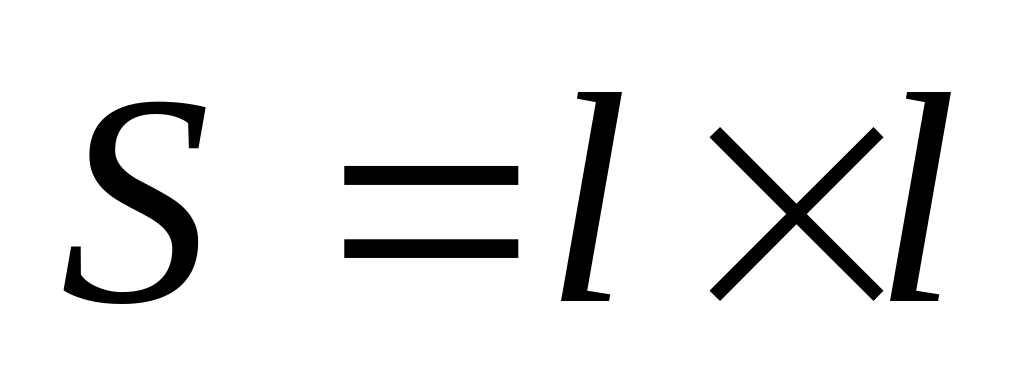, совпадающий по форме и размерам с используемым электронагревателем (на рис. 6.8, а электронагреватель условно обозначен позицией 3), размещаемым на левой грани образца 1.

2. Исследуемый образец 1 зажимают (с постоянной силой – для уменьшения влияния термических сопротивлений) между электронагревателем 3 и медной пластиной 2.

Получившуюся систему необходимо некоторое время выдержать при заданной температуре для получения необходимого начального распределения температуры как в образце 1, так и в медной пластине 2.

3. В момент начала активной стадии эксперимента на электронагреватель 3 подают постоянную электрическую мощность, что позволяет с достаточной точностью задать постоянную во времени величину теплового потока

Примечание. В этом случае лучше использовать два образца 1 и две медные пластины 2, размещаемые симметрично относительно нагревателя 3.

Возможен вариант, когда система программного регулирования, за счет изменения электрической мощности (подводимой к электронагревателю 3), обеспечивает изменение во времени температуры левой грани образца 1 по линейному закону

4. На протяжении всей активной стадии эксперимента выполняют измерение и регистрацию изменения во времени:

1) температур и на левой и на правой гранях исследуемого образца;

2) если есть возможность, осуществляют:

– либо непосредственное измерение величины теплового потока по электрической мощности , подводимой к электронагревателю 3, и его площади ;

– либо косвенное измерение теплового потока

по скорости изменения температуры медного ядра (пластины 2) с известными удельной теплоемкостью и массой .

В ряде случаев при выполнении расчетов удобнее использовать величину полной теплоемкости медного ядра 2.

5 Активную часть эксперимента завершают в момент времени, когда температура левой грани исследуемого образца 1 достигает определенное заранее известное значение, обычно задаваемое на несколько градусов ниже температуры деструкции исследуемого материала.

6 После завершения эксперимента осуществляют обработку полученных данных и вычисляют искомые теплофизические свойства по приведенным ниже расчетным зависимостям.