6. Силовой расчет группы звеньев 2,3.

Выделим из механизма группу звеньев 2,3 и расставим все нагрузки: силы тяжести, силы и моменты сил инерции, реакции отброшенных звеньев. В точке В действует сила она равна полученной ранее силе и направлена противоположно ей (рис.10).

Неизвестными величинами являются: сила взаимодействия первого и второго звеньев , сила взаимодействия третьего звена и стойки , сила взаимодействия второго и третьего звеньев .

Ввиду того, что ни величина, ни направление силы неизвестны, определим ее по двум составляющим: тангенциальной , направленной перпендикулярно звену ВД, и нормальной , параллельной звену ВД. Тангенциальная составляющая определяется из условия равновесия группы звеньев 2,3. Приравняв нулю сумму моментов относительно точки Д, найдем :

откуда

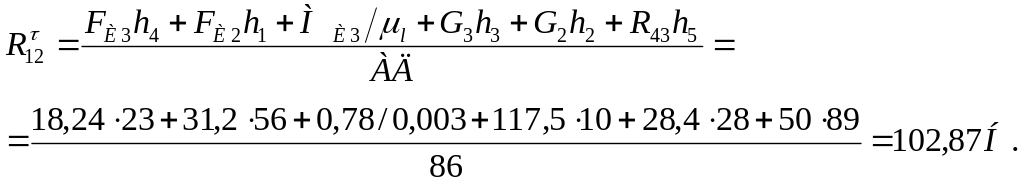
Нормальную составляющую получим из векторного многоугольника, построенного для звена 2. И этого же многоугольника определится сила взаимодействия звеньев 3 и 2 - . Определение указанных сил возможно вследствие того, что известны их направления: сила параллельна звену ВС, а сила - перпендикулярна ему. Построив силовой многоугольник (рис.11), получим искомые силы:

Реакция стойки (опоры Д) определится после построения силового многоугольника для звена 3 (рис.12):

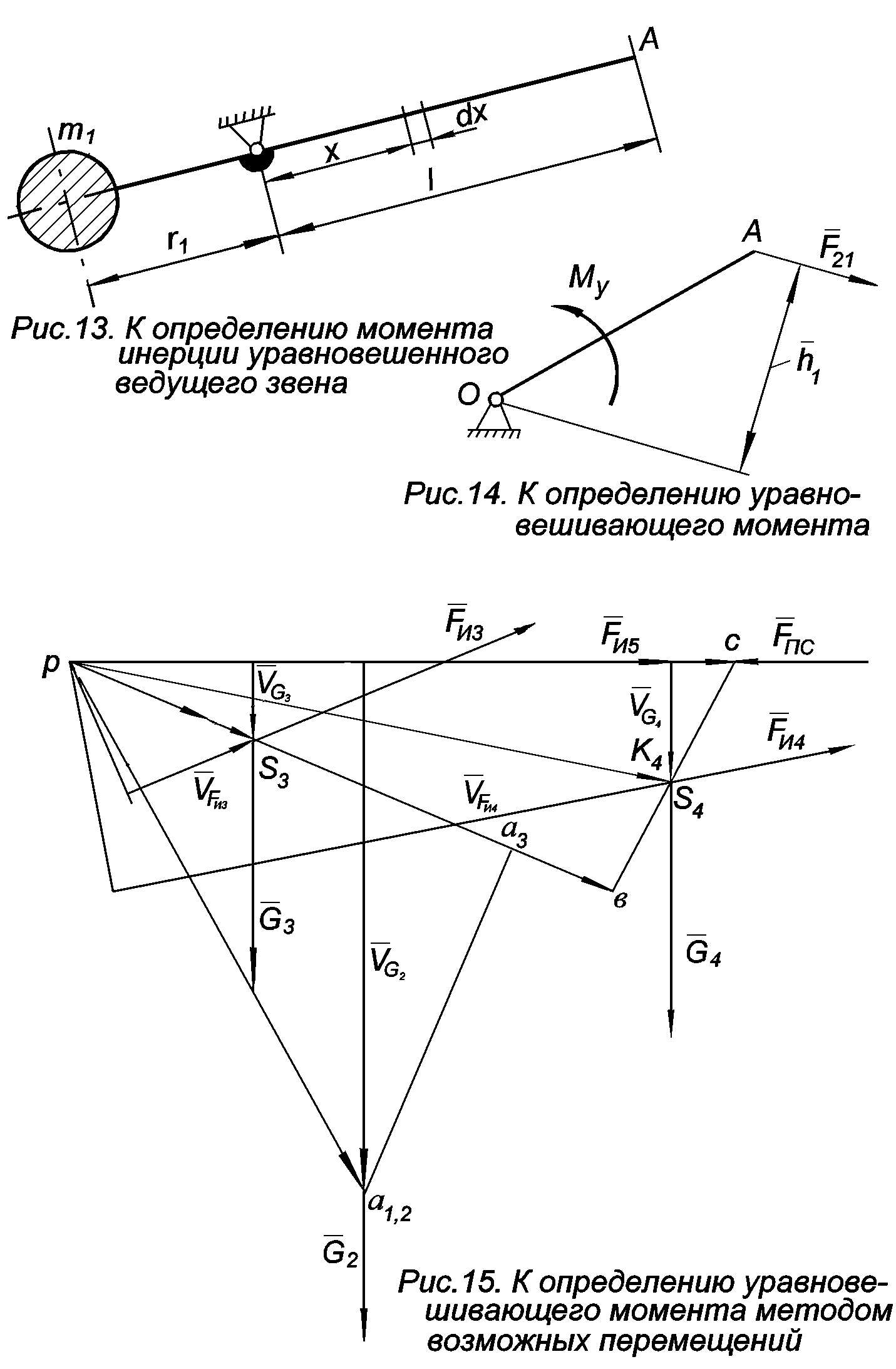
7. Силовой расчет ведущего звена.

Ведущее звено обычно уравновешено, то есть центр масс его находится на оси вращения (рис.13) . Для этого требуется, чтобы сила инерции противовеса , установленного на продолжении кривошипа АО, равнялась силе инерции звена ОА:

где масса звена ОА, кг;

масса противовеса, кг;

масса единицы длины ( )кг.

Отсюда можно определить массу противовеса, задавшись её расстоянием от оси вращения. При ; .

В точке А со стороны второго звена на первое действует сила , момент которой относительно точки О равен уравновешивающему моменту (рис.14):

В точке О при этом возникает реакция , равная и противоположно направленная силе . Если сила тяжести первого звена соизмерима с силой , то её необходимо учесть при определении реакции опоры О, которая может быть получена из векторного уравнения:

где: .

8. Определение уравновешивавшего момента методом возможных перемещений.

Из курса теоретической механики известно, что сумма элементарных работ на возможных перемещениях системы с идеальными связями, находящейся в равновесии, равна нулю (принцип возможных перемещений). Направления элементарных перемещений точек механизма совпадает с направлением скоростей этих точек. Легко показать, что в этом случае удовлетворяется условие равенства нулю мгновенных мощностей, если разделить все работы на время, которое нулю не равно.

По плану скоростей находят скорости тех точек механизма, к которым приложены силы. Если к звеньям приложены моменты сил, то действие их следует учесть изменением точки приложения какой-либо силы, как было показано на примере замены силы инерции и момента силы инерции одной силой (рис.3), либо определить мгновенную мощность момента как произведения его на угловую скорость звена, к которому этот момент приложен.

По известным величинам и направлениям сил и скоростей вычисляется сумма мгновенных мощностей нагрузок, приложенных к механизму и приравнивается нулю, откуда и определяется уравновешивающая сила или уравновешивающий момент.

Пример: К плану скоростей (рис.15) приложим в соответствующих точках силы, действую-

щие на звенья механизма. Следует заметить, что силы можно прикладывать в любой точке плана, так как важны лишь их направления. Затем спроектируем скорости точек приложения сил на направления этих сил. При этом проекции скоростей обозначим индексами тех сил, на направления которых векторы-скорости спроектированы. Например, означает проекцию скорости точки приложения силы на направление этой силы.

Подставив полученные мощности в уравнение:

,

получим:

Знаки определяются направлением векторов сил и проекций скоростей на эти силы. Минус – только для мощности силы полезного сопротивления.

откуда:

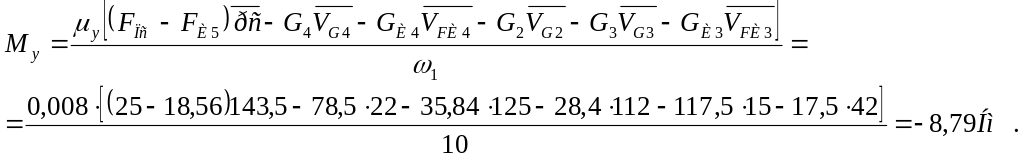
Знак «минус» показывает, что уравновешивающий момент направлен противоположно угловой скорости входного звена .

Относительная погрешность двух методов определения уравновешивающего момента:

На рис.15 не показаны силы и , т.к. их мощности равны нулю вследствие перпендикулярности векторов сил и скоростей.

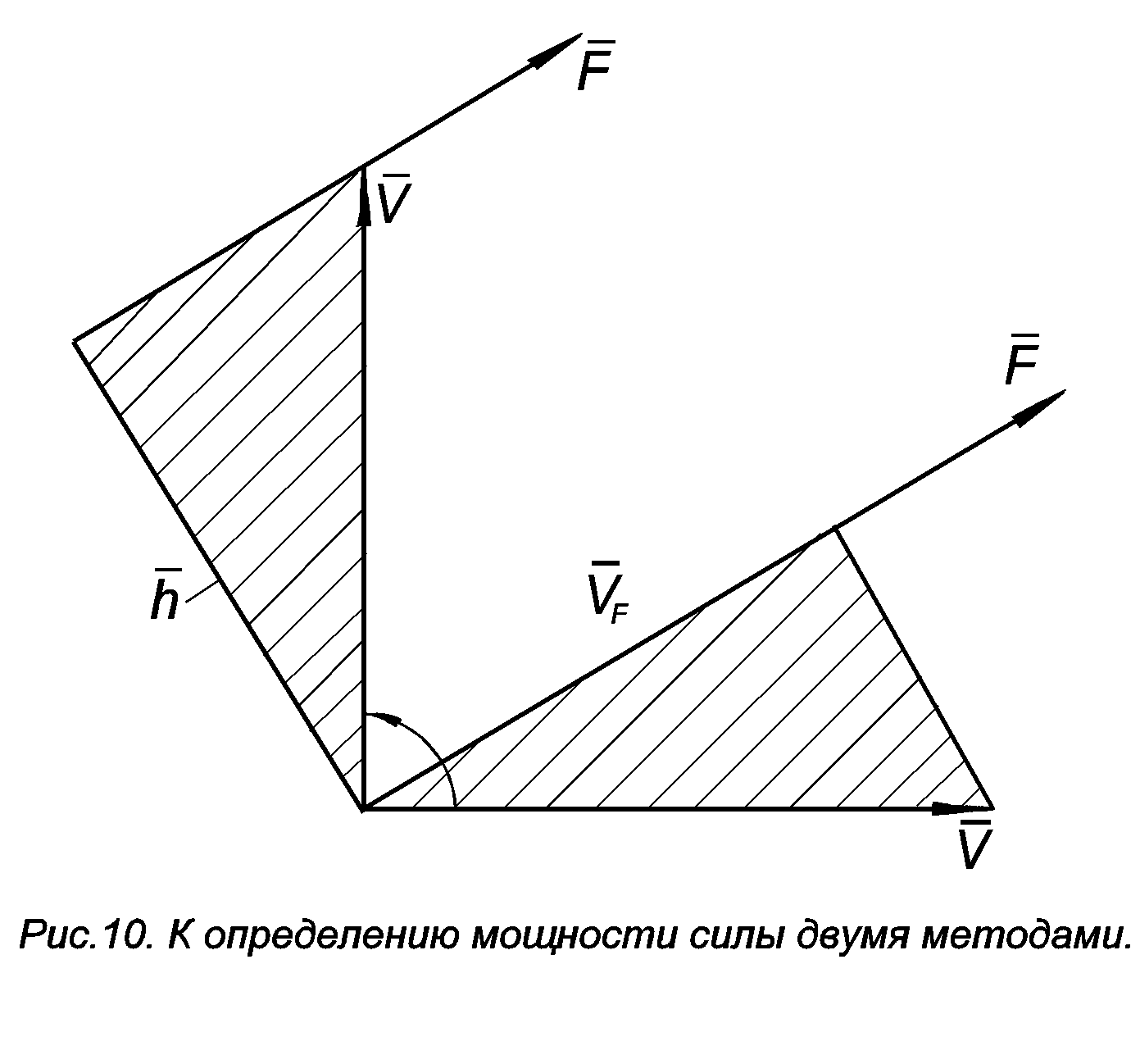
В методе Н.Е. Жуковского мощности сил находятся как произведения сил на их расстояния до полюса повернутого плана скоростей. Из рис.16 видно, что при повороте вектора скорости на 90⁰ заштрихованные треугольники совместятся так, что , то есть в обоих методах находятся произведения одних и тех же величин.

Очевидны недостатки метода Н.Е. Жуковского:

• дополнительная работа и погрешности, связанные с поворотом плана;

• потеря физического смысла и возможности логического обоснования необходимости поворота плана скоростей;

• трудности определения знака мощности, так как в зависимости от направления поворота угол между векторами силы и скорости будет острым или тупым, а знак определится положением этих векторов при неповернутом плане скоростей.

15