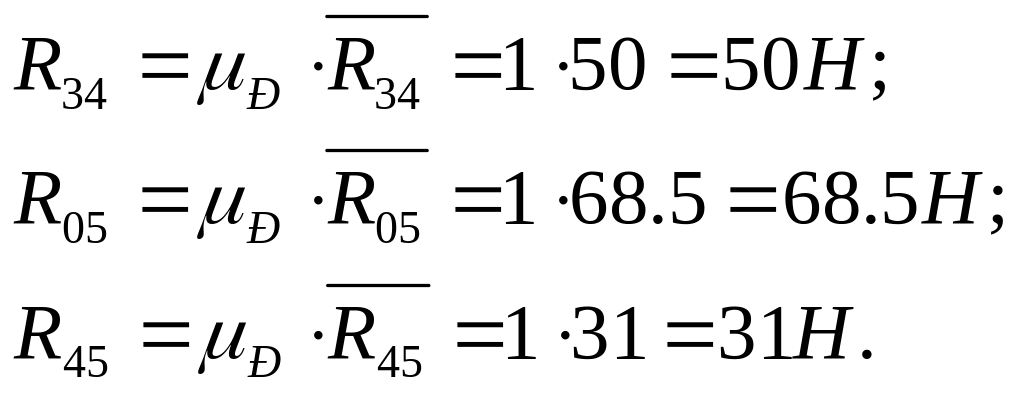5. Силовой расчет группы звеньев 4 и 5.

Выделим из механизма группу звеньев 4 и 5 , расставим все реальные нагрузки и фиктивные – силы и моменты сил инерции (рис.8).Действие на рассматриваемую группу отброшенных звеньев механизма заменим силами. В точке С на ползун 5 действует сила со стороны стойки – направляющей ползуна. В отсутствии трения сила взаимодействия направлена перпендикулярно направлению движения ползуна, а вниз или вверх, пока неизвестно, поэтому направим эту силу предварительно вверх. Если после вычислений окажется, что она отрицательна, то необходимо изменить направление на противоположное.

В индексе обозначения силы ставятся две цифры: первая показывает со стороны какого звена действует сила, а вторая- на какое звено эта сила действует.

В точке В со стороны звена 3 на звено 4 действует сила . Ни величина, ни направление этой силы неизвестны, поэтому определяем её по двум составляющим: одну направим вдоль звена и назовем нормальной составляющей , а вторую перпендикулярно звену и назовем тангенциальной составляющей . Предварительно направление этих составляющих выбираем произвольно, а действительное направление определится знаком силы после вычислений.

На ползун С действует сила полезного сопротивления , величина которой определена ранее.

Расставим на выделенной группе звеньев 4 и 5 все перечисленные силы и определим неизвестные реакции в кинематических парах В и С - и .

Сначала определяется тангенциальная составляющая силы - из условия равновесия звена 4. Приравняв нулю сумму моментов сил относительно точки С, получим:

;

откуда:

Знак “минус” показывает, что действительное направление силы противоположно предварительно принятому. Момент сил инерции необходимо делить на масштаб длин потому, что величины ВС изображены в масштабе , и в расчетах используются их значения, снятые с чертежа. Либо момент оставить в истинную величину, а все длины умножить на масштаб .

Нормальная составляющая силы и сила определяются графическим методом из одного векторного многоугольника, построенного для группы звеньев 4 и 5. Известно, что при силовом равновесии многоугольник, составленный из векторов сил, должен быть замкнутым:

Так как направления линий действия сил и известны (первая направлена параллельно звену ВС, а вторая перпендикулярно траектории движения ползуна), то построив предварительно незамкнутый многоугольник из известных векторов – сил, можно обеспечить его замыкание, если провести через начало первого и конец последнего вектора прямые параллельные направлениям искомых сил и .Точка пересечения этих прямых определит величины векторов и и их действительные направления (рис.9).

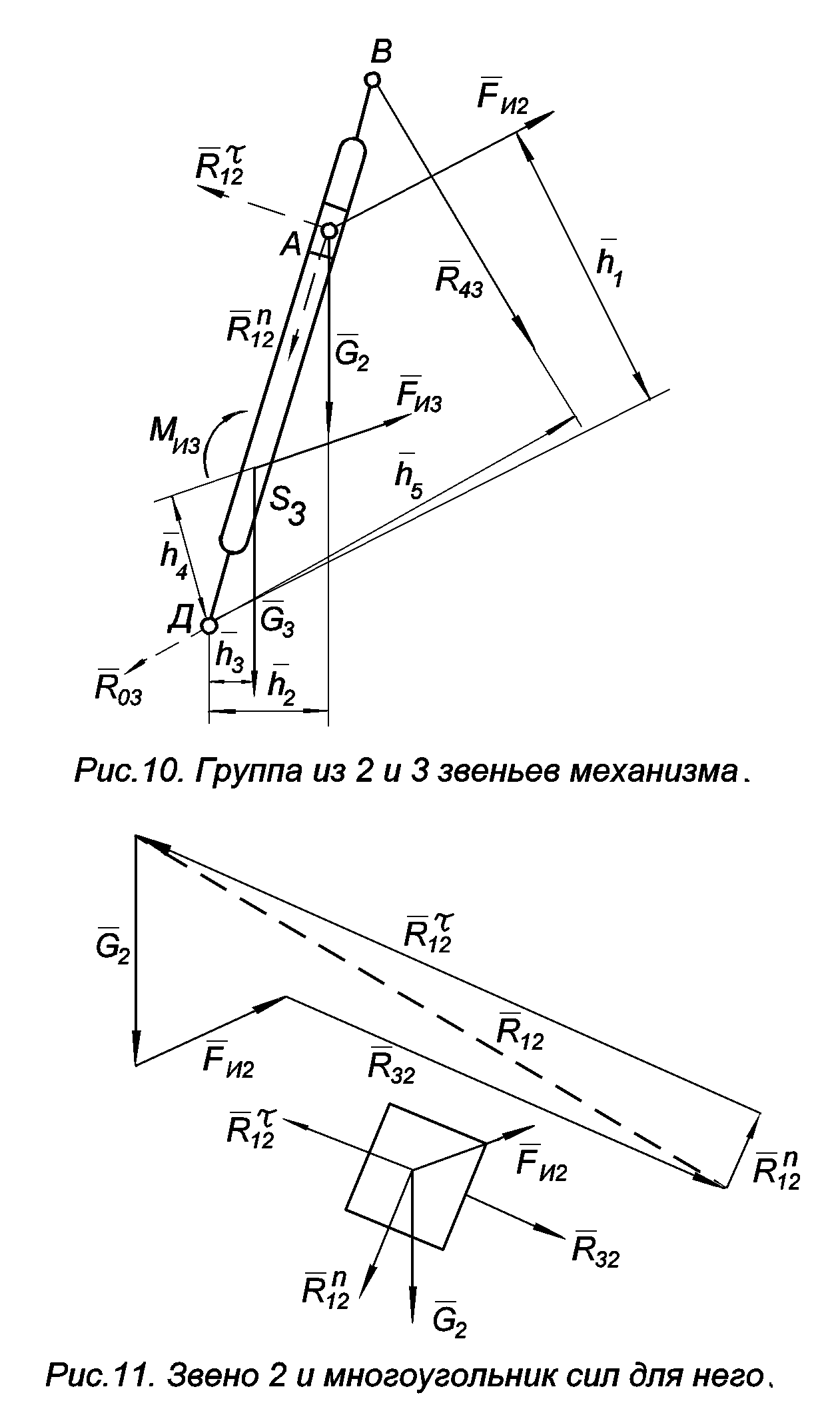
Для определения силы необходимо, чтобы составляющие ее векторы и

оказались сразу сложенными, поэтому построение многоугольника необходимо начинать с вектора .

Кроме того следует иметь ввиду, что если расположить сначала все силы действующие на звено 4, а затем на звено 5, то из такого силового многоугольника можно определить силу взаимодействия звеньев 4 и 5 (пунктирная прямая m – n на рис.9), так как в этом случае многоугольник сил, соответствующий равновесию двух звеньев, можно разделить на два многоугольника, соответствующих равновесию каждого звена в отдельности.

Условие равновесия звена 4 требует, чтобы:

Условие равновесия звена 5 требует, чтобы:

где .

Из построений видно, что направление силы - от n к m , а силы от m к n.

Определим величины реакций в кинематических парах: