4. Пример расчета для 6-го положения механизма.

Дано: - длины звеньев:

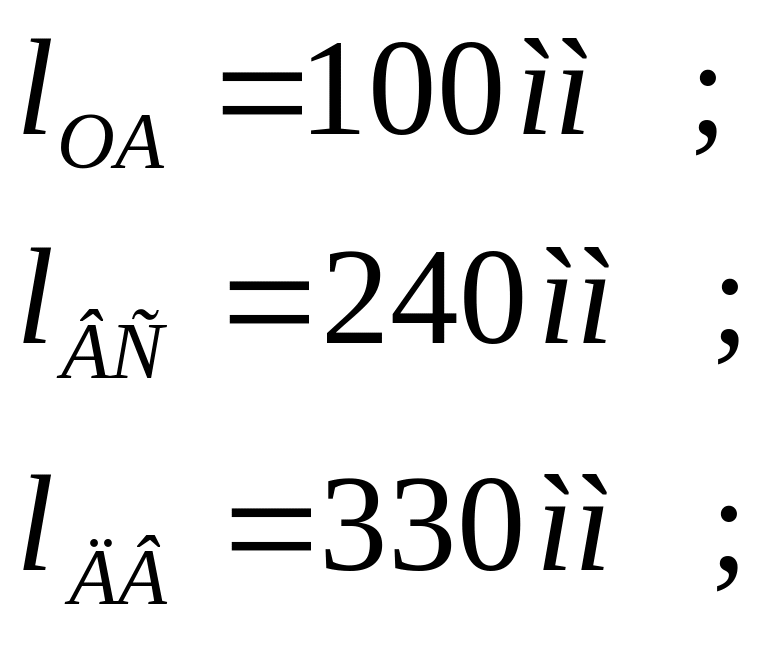
- массы звеньев:

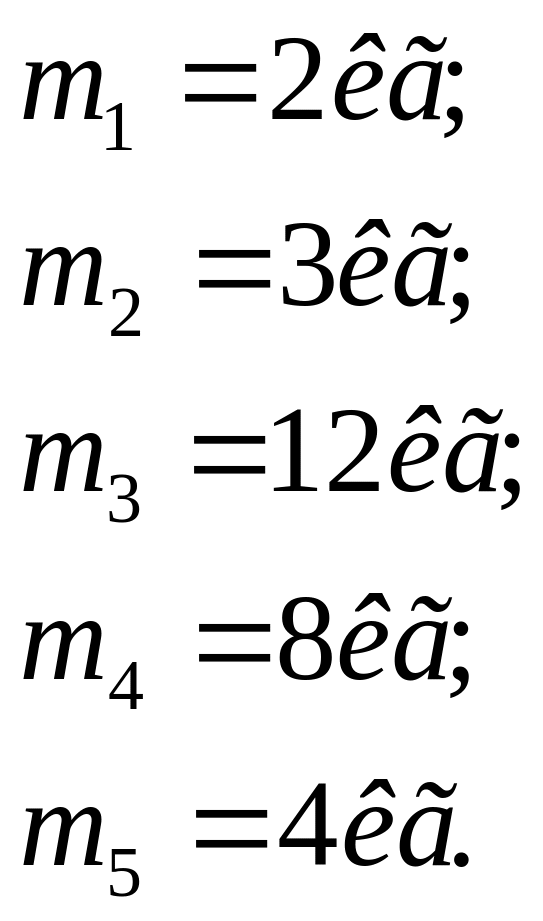
- диаграмма сил полезных сопротивлений (рис.6);

- угловая скорость входного звена .

Часто задается масса единицы длины звена в этом случае массы звеньев находятся умножением длин звеньев на погонную массу .

Определить реакции в кинематических парах и уравновешивающий момент на выходном валу механизма (рис. 1).

4. 1. Определение нагрузок действующих на звенья

4.1.1.Определение реальных нагрузок.

Вычислим силы тяжести. Равнодействующие этих сил приложены в центрах масс звеньев, а величины равны:

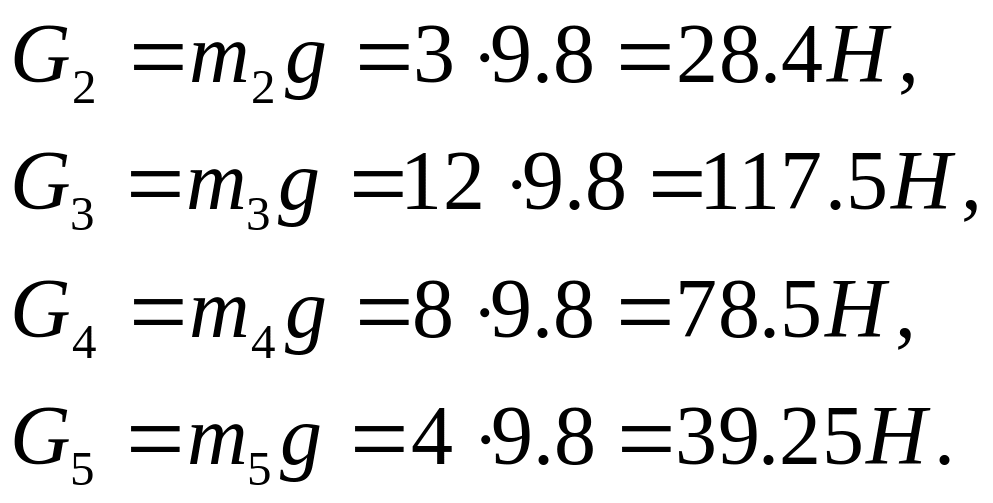
Найдем силу полезного сопротивления по диаграмме (рис.6).

Для рассматриваемого (шестого) положения механизма получим:

Направление этой силы противоположного скорости ползуна – звена 5.

Данных для вычисления сил вредных сопротивлений нет, поэтому их не учитываем.

4.1.2. Определение инерционных (фиктивных нагрузок).

Для определения инерционных нагрузок требуются ускорения звеньев и некоторых точек, поэтому воспользуемся планом ускорений для рассматриваемого положения механизма (рис.2).

Выясним характер движения звеньев механизма. Два звена - ползун 2 и шатун 4 совершают плоскопараллельные движения. Ползун 5 движется поступательно, кулиса3 и кривошип 1 – вращаются. Так как размерами ползунов пренебрегают и считают их точечными массами, то ползун 2, в этой связи, имеет только вращательное движение вместе с кривошипом 1.У кулисы 3 и шатуна 4 в качестве точек ,совершающих переносные движения , примем центры масс звеньев и , лежащие соответственно на 1/3 длины звена 3 и посередине длины звена 4.

Определим силы инерции звеньев. Ведущее звено, как правило, уравновешено , то есть центр масс его лежит на оси вращения, а равнодействующая сил инерции равна нулю. Для определения сил инерции других звеньев механизма предварительно определим ускорения их центров масс:

где -масштаб плана ускорений, :

- вектор - отрезок, изображающий ускорение точки , мм.

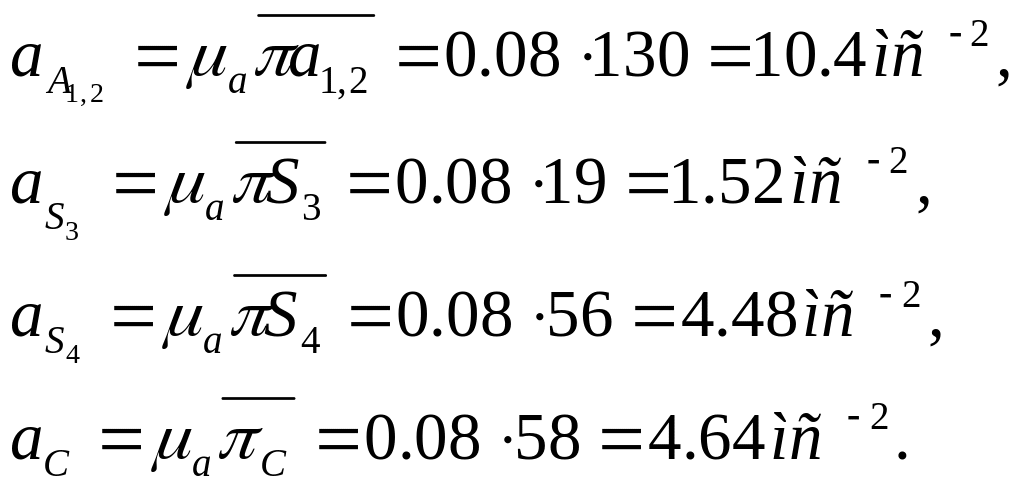
Теперь определим силы инерции: ,

где - масса i -го звена ,кг;

- ускорение центра масс,мс^-2.

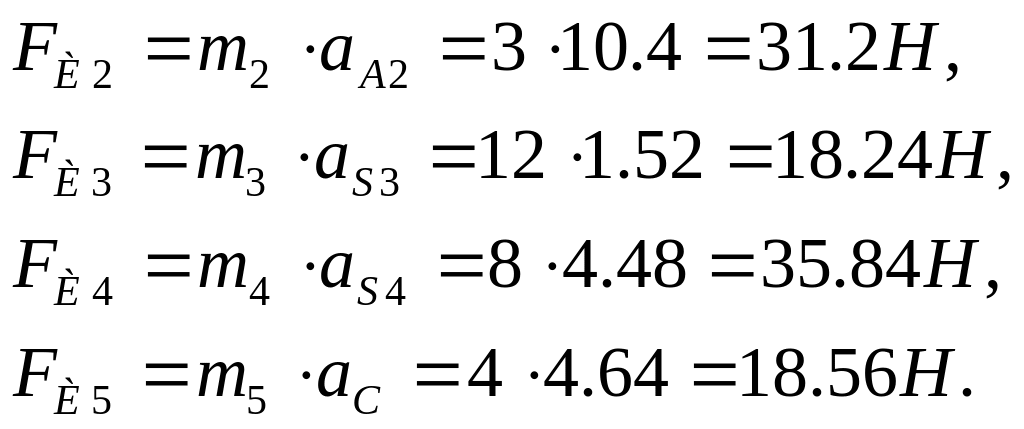
Для определения моментов сил инерции необходимо найти моменты инерции масс звеньев и их угловые ускорения. У звеньев 2 и 5 массы сосредоточены в точках, а у звена 1 угловое ускорение равно нулю, поэтому моменты сил инерции этих звеньев равны нулю.

Примем распределение массы звена 3 по треугольнику, звена 4 – равномерно по длине, тогда момент инерции массы звена 3 относительно точки найдем по раннее полученной зависимости:

Момент инерции массы звена 4 относительно точки равен:

Вообще характер распределения массы по длине звена определяется его конструкцией, выполненной на основе силового, прочностного и других расчетов.

Поэтому для получения меньшей ошибки в расчетах необходимо предварительно ознакомится с конструкциями механизмов аналогичных проектируемому, обратив внимание на формы звеньев и распределение их масс.

Угловые ускорения звеньев 3 и 4 определяются по относительным тангенциальным ускорениям и , векторы которых изображены на плане ускорений отрезками - и соответственно, поэтому:

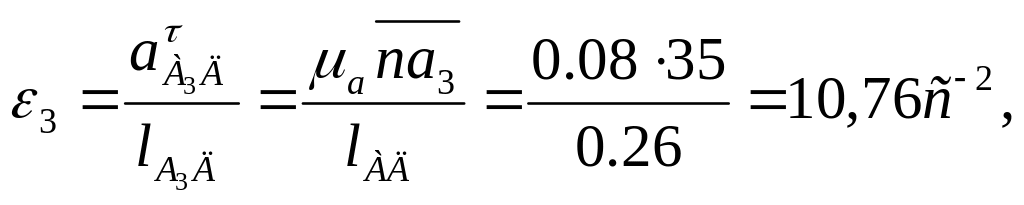
Найдем моменты сил инерции 3-го и 4-го звеньев: