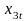2.3. Задания для самостоятельной работы
Задание 2.3.1. Владельцы интернет-аукциона «Э-Слава» составляют бизнес-план своей деятельности на следующие два месяца. Их прежде всего интересует вопрос, каким образом можно увеличить объем реализации в натуральном выражении. В ходе исследования было выявлено, что на количество совершаемых в среднем за месяц покупок ( ) влияют такие факторы, как затраты на баннерную рекламу (тыс. руб., ), расходы на мероприятия, осуществляемые с целью привлечения интернет-пользователей на сайт аукциона (тыс. руб., ), и число зарегистрированных пользователей сайта ( ). Поэтому было решено построить модель множественной регрессии, отражающую зависимость количества покупок от указанных факторов. Данные об этих показателях за последние 20 месяцев представлены в табл. 2.3.1.
Т а б л и ц а 2.3.1
|
|
|
|
|
|
|
|
|
|
1 |
535 |
8,39 |
30,31 |
985 |
11 |
561 |
6,58 |
23,78 |
772 |
2 |
515 |
6,83 |
24,68 |
802 |
12 |
388 |
4,48 |
16,17 |
525 |
3 |
382 |
5,54 |
20,00 |
650 |
13 |
630 |
7,41 |
26,76 |
869 |
4 |
721 |
8,47 |
30,59 |
994 |
14 |
769 |
8,55 |
30,88 |
1003 |
5 |
276 |
6,13 |
22,13 |
719 |
15 |
470 |
5,52 |
19,95 |
648 |
6 |
513 |
5,77 |
20,85 |
677 |
16 |
511 |
6,01 |
21,7 |
705 |
7 |
664 |
7,80 |
28,18 |
915 |
17 |
549 |
6,19 |
22,36 |
726 |
8 |
409 |
4,80 |
17,35 |
563 |
18 |
531 |
8,85 |
31,96 |
1038 |
9 |
537 |
5,42 |
19,57 |
636 |
19 |
499 |
7,21 |
26,05 |
846 |
10 |
794 |
9,31 |
33,62 |
1092 |
20 |
503 |
5,99 |
21,65 |
703 |
Задание 2.3.2. Фирма «Ваше очарование» довольно успешно осуществляет торговлю косметическими товарами на российском рынке. Ее успех определяется, в частности, человеческим фактором. С целью изучения его влияния на среднеквартальный объем продаж (млн. руб., ) через такие показатели, как фонд оплаты труда (млн. руб., ) и численность работников фирмы (чел., ), была сформирована табл. 2.3.2. В этой таблице приведены данные по этим показателям за последние 18 кварталов. Постройте двухфакторную регрессионную модель, отражающую зависимость объема продаж от указанных факторов.
Т а б л и ц а 2.3.2
|
|
|
|
|
|
|
|
1 |
39832 |
3975 |
1986 |
10 |
43671 |
4344 |
2171 |
2 |
33527 |
3337 |
1668 |
11 |
39518 |
3895 |
1946 |
3 |
36181 |
3586 |
1792 |
12 |
47639 |
4941 |
2469 |
4 |
42873 |
4065 |
2031 |
13 |
39518 |
3895 |
1946 |
5 |
28279 |
2859 |
1429 |
14 |
29376 |
2919 |
1458 |
6 |
52256 |
5001 |
2499 |
15 |
28215 |
2809 |
1404 |
7 |
36425 |
3611 |
1805 |
16 |
33193 |
3298 |
1648 |
8 |
27734 |
2760 |
1379 |
17 |
33927 |
3377 |
1688 |
9 |
54547 |
5419 |
2708 |
18 |
57736 |
5250 |
2624 |
Задание 2.3.3. В табл. 2.3.3 представлены данные о продажах квартир на вторичном рынке жилья. В этой таблице приняты следующие обозначения:
– цена квартиры, тыс. долл.;
– число комнат в квартире;
– район города (1 – центральный, 0 – периферийный);
– общая площадь квартиры (кв. м.);
– жилая площадь квартиры (кв. м.);
– площадь кухни (кв.м.);
–
тип
дома (1 – кирпичный, 0 – другой);
–
расстояние
от метро (минут, пешком).
Составьте матрицу парных коэффициентов корреляции и установите: 1) наиболее значимо влияют на цену; 2) какие из факторов коллинеарны. Устранив мультиколлинеарность, постройте линейное уравнение регрессии, характеризующее зависимость от соответствующих факторов. Оцените качество построенного уравнения.
Т а б л и ц а 2.3.3
№ п.п. |
|
|
|
|
|
|
|
|
-1- |
-2- |
-3- |
-4- |
-5- |
-6- |
-7- |
-8- |
-9- |
1. |
13,0 |
1 |
1 |
37,0 |
21,5 |
6,5 |
0 |
20 |
2. |
16,5 |
1 |
1 |
60,0 |
27,0 |
22,4 |
0 |
10 |
3. |
17,0 |
1 |
1 |
60,0 |
30,0 |
15,0 |
0 |
10 |
4. |
15,0 |
1 |
1 |
53,0 |
26,2 |
13,0 |
0 |
15 |
5. |
14,2 |
1 |
1 |
35,0 |
19,0 |
9,0 |
0 |
8 |
6. |
10,5 |
1 |
1 |
30,3 |
17,5 |
5,6 |
1 |
15 |
7. |
23,0 |
1 |
1 |
43,0 |
25,5 |
8,5 |
0 |
5 |
8. |
11,3 |
1 |
0 |
31,0 |
18,0 |
5,5 |
1 |
10 |
О к о н ч а н и е т а б л. 2.3.3
-1- |
-2- |
-3- |
-4- |
-5- |
-6- |
-7- |
-8- |
-9- |
9. |
13,0 |
1 |
0 |
33,0 |
19,6 |
7,0 |
0 |
5 |
10. |
21,0 |
1 |
0 |
53,0 |
26,0 |
16,0 |
1 |
5 |
11. |
12,0 |
1 |
0 |
32,2 |
18,0 |
6,3 |
0 |
20 |
12. |
11,0 |
1 |
0 |
31,0 |
17,3 |
5,5 |
1 |
15 |
13. |
11,0 |
1 |
0 |
36,0 |
19,0 |
8,0 |
1 |
5 |
14. |
15,6 |
1 |
1 |
35,0 |
18,0 |
5,3 |
1 |
3 |
15. |
26,0 |
2 |
1 |
55,5 |
35,0 |
8,0 |
0 |
10 |
16. |
18,5 |
2 |
1 |
48,0 |
28,0 |
8,0 |
0 |
10 |
17. |
13,2 |
2 |
1 |
44,1 |
30,0 |
6,0 |
1 |
25 |
18. |
25,8 |
2 |
1 |
80,0 |
51,0 |
13,0 |
0 |
10 |
19. |
17,0 |
2 |
1 |
60,0 |
38,0 |
19,0 |
0 |
12 |
20. |
18,0 |
2 |
0 |
50,0 |
30,0 |
8,7 |
1 |
15 |
21. |
21,0 |
2 |
0 |
54,6 |
32,0 |
5,5 |
1 |
20 |
22. |
14,5 |
2 |
0 |
43,0 |
27,0 |
12,0 |
1 |
10 |
23. |
23,0 |
2 |
0 |
66,0 |
39,0 |
7,0 |
1 |
5 |
24. |
19,5 |
2 |
0 |
53,5 |
29,5 |
6,0 |
1 |
15 |
25. |
14,2 |
2 |
0 |
45,0 |
29,0 |
6,0 |
1 |
12 |
26. |
13,3 |
2 |
0 |
45,0 |
30,0 |
5,5 |
0 |
5 |
27. |
16,1 |
2 |
0 |
50,6 |
30,8 |
7,9 |
0 |
10 |
28. |
13,5 |
2 |
0 |
42,5 |
28,0 |
5,2 |
0 |
25 |
29. |
15,5 |
3 |
1 |
68,1 |
44,4 |
7,2 |
0 |
5 |
30. |
38,0 |
3 |
1 |
107,0 |
58,0 |
24,0 |
0 |
15 |
31. |
30,0 |
3 |
1 |
100,0 |
58,0 |
20,0 |
0 |
15 |
32. |
24,0 |
3 |
1 |
71,0 |
52,0 |
7,5 |
1 |
15 |
33. |
32,5 |
3 |
1 |
98,0 |
51,0 |
15,0 |
0 |
10 |
34. |
43,0 |
3 |
0 |
100,0 |
45,0 |
35,0 |
1 |
25 |
35. |
17,8 |
3 |
0 |
58,0 |
39,0 |
6,2 |
0 |
10 |
36. |
28,0 |
3 |
0 |
75,0 |
40,0 |
18,0 |
1 |
3 |
37. |
32,7 |
3 |
0 |
85,0 |
59,0 |
9,0 |
0 |
5 |
38. |
31,0 |
3 |
0 |
66,0 |
48,0 |
6,0 |
0 |
2 |
39. |
16,0 |
3 |
0 |
80,0 |
54,0 |
8,0 |
0 |
3 |
40. |
22,0 |
3 |
0 |
62,0 |
37,0 |
10,2 |
1 |
5 |
41. |
23,0 |
3 |
0 |
69,7 |
42,0 |
10,8 |
0 |
15 |
42. |
19,5 |
3 |
0 |
79,0 |
50,3 |
9,1 |
1 |
25 |
43. |
24,5 |
4 |
1 |
90,0 |
64,0 |
15,0 |
0 |
5 |
44. |
27,3 |
4 |
1 |
102,0 |
66,0 |
11,8 |
0 |
7 |
45. |
41,0 |
4 |
1 |
87,0 |
56,5 |
12,5 |
0 |
10 |
46. |
31,0 |
4 |
1 |
114,8 |
74,0 |
25,6 |
0 |
10 |
47. |
35,6 |
4 |
1 |
114,3 |
74,7 |
12,0 |
1 |
5 |
48. |
46,0 |
4 |
1 |
90,0 |
62,0 |
8,0 |
1 |
5 |
49. |
35,0 |
4 |
1 |
116,0 |
81,0 |
16,5 |
0 |
10 |
50. |
35,6 |
4 |
1 |
107,0 |
75,5 |
9,5 |
0 |
10 |
51. |
46,0 |
4 |
0 |
93,0 |
66,0 |
10,0 |
0 |
15 |
52. |
35,0 |
4 |
0 |
176,0 |
129,0 |
15,0 |
0 |
10 |
53. |
26,5 |
4 |
0 |
74,7 |
50,8 |
8,2 |
1 |
10 |
54. |
37,0 |
4 |
0 |
115,0 |
76,0 |
8,5 |
0 |
5 |
55. |
30,0 |
4 |
0 |
92,0 |
62,0 |
9,0 |
0 |
15 |
56. |
43,0 |
4 |
0 |
110,0 |
79,5 |
10,0 |
0 |
5 |
Задание 2.3.4. Для линейного трехфакторного уравнения регрессии имеются данные, представленные в табл. 2.3.4. Выполните следующие задания: 1) определите корреляционную матрицу R и содержащийся в этих данных размер коллинеарности как det(R); 2) рассчитайте размер коллинеарности, в случае если из уравнения выводится переменная ; 3) вычислите гребневые оценки параметров для гребневой константы, равной 0,5 и 0,8.
Т а б л и ц а 2.3.4
|
10,3 |
14,6 |
11,4 |
17,1 |
10,6 |
|
20,8 |
28,0 |
23,0 |
30,5 |
21,7 |
|
4,1 |
20,3 |
9,8 |
8,1 |
17,7 |
|
40,0 |
80,0 |
55,0 |
58,0 |
70,0 |
Задание
2.3.5. По
данным табл. 2.3.5 изучается зависимость
индекса качества жизни населения (
)
от следующих показателей
социально-экономического развития
регионов:
–
ВРП (с учётом уровня покупательной
способности) на душу населения (тыс.
руб.);
–
объём внешнеторгового оборота на душу
населения (млн. долл. США);
–
финансовая обеспеченность региона (с
учётом уровня покупательной способности)
на душу населения (тыс. руб.);
–
общий объём розничного товарооборота
и платных услуг (с учётом уровня
покупательной способности) на душу
населения (тыс. руб.);
–
объём инвестиций в основной капитал на
душу населения (тыс. руб.);
–
доля занятых на малых предприятиях в
общей численности занятых в экономике
(% к общей численности занятых в экономике);
–
основные фонды отраслей экономики (по
полной балансовой стоимости, с учётом
степени удорожания капитальных затрат)
на душу населения (тыс. руб.); коэффициент
плотности автомобильных дорог (коэффициент
Энгеля);
–
уровень регистрируемой безработицы (%
к экономически активному населению);
–соотношение
среднедушевых доходов и среднедушевого
прожиточного минимума;
–
доля населения с доходами ниже прожиточного
минимума (%);
–
обеспеченность местами детей, находящихся
в дошкольных учреждениях (мест на 1000
детей дошкольного возраста);
–
выпуск специалистов высшими и
государственными средними учебными
заведениями (спец. на 10000 чел. населения);
–
обеспеченность населения врачами и
средним мед. персоналом (на 10000 ед.
населения);
–
обеспеченность населения
амбулаторно-поликлиническими учреждениями
(число посещений за смену на 10000 чел.).
Требуется: 1) построить матрицу парных коэффициентов. Рассчитать коэффициенты множественной детерминации, используя в качестве зависимой переменной каждый фактор. Установить, какие факторы мультиколлинеарны; 2) построить уравнение множественной регрессии с полным набором факторов и оценить его качество; 3) отобрать наиболее информативные факторы и построить уравнение регрессии со статистически значимыми факторами.
Т а б л и ц а 2.3.5
Регион |
|
|
|
|
|
|
|
|
г, Москва |
159,71 |
4,99 |
67,37 |
100,49 |
25,39 |
31 |
212,37 |
34,12 |
г, Санкт-Петербург |
80,34 |
1,87 |
40,97 |
42,27 |
20,11 |
26,17 |
127 |
56,86 |
Самарская область |
84,67 |
1,84 |
37,07 |
52,59 |
11,7 |
15,83 |
159,58 |
16,63 |
Липецкая область |
98,17 |
1,6 |
60,19 |
34,64 |
11,92 |
5,75 |
141,92 |
28,4 |
Ханты-Мансийский автономный округ |
315,69 |
13,18 |
199,46 |
44,88 |
61,74 |
4,83 |
471,3 |
2,31 |
Республика Татарстан |
92,37 |
1,08 |
42,97 |
39,43 |
14,3 |
5,22 |
103,97 |
26,21 |
Республика Коми |
83,62 |
1,44 |
38,06 |
40,93 |
13,29 |
8,18 |
170,8 |
7,85 |
Ямало-Ненецкий автономный округ |
440,67 |
6,1 |
141,96 |
39,85 |
166,2 |
5,29 |
166,94 |
1,56 |
Ярославская область |
79,91 |
0,51 |
29,65 |
28,11 |
11,08 |
7,97 |
189,5 |
33,88 |
Свердловская область |
66,89 |
0,94 |
33,43 |
39,24 |
8,68 |
10,78 |
123,86 |
11,53 |
Тюменская область |
70,91 |
1,63 |
36,14 |
40,68 |
9,76 |
9,69 |
104,73 |
8,95 |
Республика Башкортостан |
74,98 |
0,74 |
38,85 |
40,7 |
9,85 |
8,62 |
103,09 |
28,8 |
Нижегородская область |
77,19 |
0,72 |
26 |
32,64 |
9,35 |
12,14 |
92,86 |
25,74 |
Пермская область |
67,87 |
1,01 |
36,81 |
37,89 |
11,7 |
4,15 |
171,56 |
16,27 |
Московская область |
63,19 |
0,98 |
26,37 |
35,39 |
13,69 |
13,07 |
147,96 |
29,92 |
О к о н ч а н и е т а б л. 2.3.5
Регион |
|
|
|
|
|
|
|
|
г. Москва |
1,24 |
10,01 |
20 |
73 |
174,55 |
208,9 |
418,4 |
0,711 |
г. Санкт-Петербург |
2,1 |
3,42 |
28 |
71,5 |
173,75 |
191,96 |
344,6 |
0,723 |
Самарская область |
1,84 |
3,4 |
29 |
76 |
106,7 |
134 |
227,6 |
0,708 |
Липецкая область |
0,69 |
2,88 |
25 |
56,75 |
76,92 |
164 |
290 |
0,705 |
Ханты-Мансийский автономный округ |
2,65 |
5,9 |
5,8 |
68,1 |
30,1 |
163,2 |
271 |
0,867 |
Республика Татарстан |
1,51 |
3,32 |
24 |
67,9 |
95,41 |
169 |
225 |
0,720 |
Республика Коми |
3,13 |
3,49 |
23,5 |
91,88 |
77 |
163,2 |
290,6 |
0,713 |
Ямало-Ненецкий автономный округ |
2,38 |
6,59 |
11 |
82 |
44,04 |
157,7 |
195 |
0,830 |
Ярославская область |
1,98 |
2,88 |
18,36 |
94 |
97,61 |
155,8 |
242 |
0,715 |
Свердловская область |
2,17 |
3,33 |
20,5 |
87,8 |
112,03 |
146,8 |
284,9 |
0,715 |
Тюменская область |
1,61 |
3,51 |
32 |
55 |
126,1 |
152 |
310 |
0,769 |
Республика Башкортостан |
1,58 |
3,15 |
26 |
60 |
93,64 |
150,2 |
228,2 |
0,704 |
Нижегородская область |
0,86 |
2,55 |
20 |
91 |
97,2 |
151 |
237,4 |
0,699 |
Пермская область |
1,5 |
3,19 |
21 |
74 |
91,98 |
172,4 |
199 |
0,704 |
Московская область |
1,76 |
2,52 |
24 |
93,4 |
58,7 |
99,1 |
249 |
0,697 |
3. О Б О Б Щ Е Н Н А Я С Х Е М А
Р Е Г Р Е С С И О Н Н О Г О А Н А Л И З А