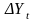4.3. Авторегрессионные модели

4.3.1. Расчетные формулы

4.3.1.1. Модель авторегрессии первого порядка AR(1):

.

4.3.1.2. Модель скользящей средней MA(1) (самостоятельно обычно не используется):

,

где .

4.3.1.3. Авторегрессионная модель скользящей средней ARMA(1,1):

,

где – ненаблюдаемая ошибка в данном уравнении.

4.3.1.4. Коэффициент автокорреляции:

.

4.3.1.5. Доверительный интервал для k-го коэффициента автокорреляции:

.

4.3.1.6. Статистика для проверки по - критерию значимости коэффициентов автокорреляции:

,

где – объем выборочной совокупности;

– максимальный рассматриваемый лаг.

4.3.1.7. Статистика для проверки значимости единичного корня по критерию Дики – Фуллера:

,

где , а – стандартная ошибка .

4.3.1.8. В случае автокорреляции остатков для проверки значимости единичного корня применяется расширенный критерий Дики – Фуллера. В расширенном критерии статистика сравнивается с критическим значением, рассчитываемым по следующей формуле:

.

Значения составляющих EDF в зависимости от уровня значимости следующие:

или ;

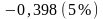или ;

или .

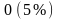Если нулевая гипотеза проверяется для модели со свободным членом

,

то строится уравнение

и расчетное значение сравнивается с критическим значением EDF, рассчитываемым при:

или ;

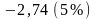или ;

или .

В тех случаях, когда модель содержит и свободный член, и тренд

,

то коэффициент определяется по уравнению

,

а критическое значение для проверки нулевой гипотезы рассчитывается при:

или ;

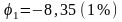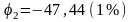или ;

или .

4.3.2. Решение типовых задач

Задание 4.3.2.1. По данным табл. 4.3.2.1, характеризующим объем продаж спортивного оборудования для футбола, постройте модель ARIMA(p, q, 0), предварительно убедившись на 95%-ном уровне значимости в интеграции данного временного ряда и определив порядок авторегрессии. С помощью построенной модели осуществите прогнозные расчеты на два последующих периода.

Т а б л и ц а 4.3.2.1

Год	Назначение оборудования:
	физические упражнения	гольф	кэмпинг	бейсбол	футбол	теннис
1992	680	740	695	580	88	255
1993	839	891	860	621	103	262
1994	1115	987	1008	665	104	271
1995	1290	1102	1130	697	118	283
1996	1434	1139	1234	707	117	294
1997	1546	1276	1340	738	126	310
1998	1654	1324	1419	742	140	367
1999	1755	1490	1490	769	151	380
2000	1825	1793	1555	778	147	259
2001	2510	2130	1612	783	159	235
2002	2890	2463	1660	789	162	240
2003	3180	2749	1700	792	171	235
2004	3400	2800	1738	796	168	215
2005	3635	2770	1765	802	174	220

Решение с помощью табличного процессора Excel.

1. Ввод исходных данных и оформление их в виде табл. 4.3.2.2.

Т а б л и ц а 4.3.2.2

	103	104	118	117	126	140	151	147	159	162	171	168	174
	88	103	104	118	117	126	140	151	147	159	162	171	168

2. Проверка временного ряда на стационарность с помощью критерия Дики – Фуллера, т.е. проверка гипотезы

,

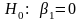значительно меньше нуля.

2.1.Оценка с помощью метода наименьших квадратов (пакета анализа данных Excel) параметров модели

.

(9,349) (0,068)

2.2. Расчет статистики

и сравнение ее с критическим значением расширенного критерия Дики – Фуллера на 95%-ном уровне значимости, равным

.

Для данного уровня значимости ряд нестационарен, так как .

2.3. Разностное представление временного ряда

и оформление результатов в виде табл. 4.3.2.3.

Т а б л и ц а 4.3.2.3

	1	14	-1	9	14	11	-4	12	3	9	-3	6
	15	1	14	-1	9	14	11	-4	12	3	9	-3

2.4. Оценка с помощью метода наименьших квадратов параметров модели

.

(2,387) (0,252)

2.5. Расчет статистики

и сравнение ее с критическим значением расширенного критерия Дики – Фуллера на 95%-ном уровне значимости

.

Для данного уровня значимости ряд стационарен, так как и, следовательно, мы имеем дело с процессом I(1).

3. Определение порядка авторегрессии для преобразованного ряда.

1. Расчет частных коэффициентов автокорреляции.

Частный коэффициент автокорреляции первого порядка равен коэффициенту автокорреляции первого порядка, т.е. . Частный коэффициент автокорреляции второго порядка равен последнему коэффициенту авторегрессионного уравнения второго порядка, т.е. для его получения необходимо построить авторегрессионное уравнение второго порядка с помощью пакета анализа Excel по данным табл. 4.3.2.4.

Т а б л и ц а 4.3.2.4

	14	-1	9	14	11	-4	12	3	9	-3	6
	1	14	-1	9	14	11	-4	12	3	9	-3
	15	1	14	-1	9	14	11	-4	12	3	9

.

Получили, что значение частного коэффициента автокорреляции резко падает, следовательно, для преобразованного временного ряда имеет смысл строить модель ARIMA(1,1,0).

2. Осуществление прогнозных расчетов по авторегрессионной модели первого порядка, построенной в п. 2.4:

,

,

,

,

.

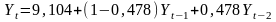Задание 4.3.2.2. Руководство плодово-овощного концерна «Витамин», владеющего большими яблоневыми садами в настоящее время желает заглянуть в перспективу, чтобы ответить на вопрос о целесообразности дальнейшего расширения этих садов. С этой целью было решено построить ARMA-модель, с помощью которой получить прогнозные оценки потребления яблок в следующие два года. Данные, отражающие динамику среднегодового потребления яблок населением г. Воронежа (y, т.), представлены в табл. 4.3.2.5.

Т а б л и ц а 4.3.2.5

T	1	2	3	4	5	6	7	8	9
Y	4980	5010	4870	4910	5860	5760	5950	6120	5050
T	10	11	12	13	14	15	16	17	18
Y	5140	5830	5970	5860	5760	5950	6120	6230	6670
T	19	20	21	22	23	24	25	26
Y	6810	6740	6930	6870	7350	7680	7820	7730

Решение табличного процессора Excel

1. Ввод исходных данных и оформление их в удобном для проведения расчетов виде.

2. Настройка параметра .

   1. 2.1. Присвоение первоначального значения параметру

.

2. Расчет преобразованных значений по следующим формулам:

, , .

(Два последних значения будут использоваться в качестве контрольной выборки для настройки параметра ).

2.3. Формирование ряда значений , .

2.4. Оформление полученных результатов в виде табл. 4.3.2.6.

Т а б л и ц а 4.3.2.6

1	4980	4980		13	5860	6521,01	6610,13
2	5010	5508	4980	14	5760	6412,10	6521,01
3	4870	5420,80	5508	15	5950	6591,21	6412,10
4	4910	5452,08	5420,80	16	6120	6779,12	6591,21
5	5860	6405,21	5452,08	17	6230	6907,91	6779,12
6	5760	6400,52	6405,21	18	6670	7360,79	6907,91
7	5950	6590,05	6400,52	19	6810	7546,08	7360,79
8	6120	6779,01	6590,05	20	6740	7494,61	7546,08
9	5050	5727,90	6779,01	21	6930	7679,46	7494,61
10	5140	5712,79	5727,90	22	6870	7637,95	7679,46
11	5830	6401,28	5712,79	23	7350	8113,79	7637,95
12	5970	6610,13	6401,28	24	7680	8491,38	8113,79

2.5. Нахождение текущих значений параметров регрессии

,

с помощью «Пакета анализа» Excel (см. Вывод итогов 4.3.2.1).

Таким образом, , , 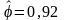а сама модель записывается в виде

.

2.6. Расчет параметров регрессии для исходного ряда

; .

Следовательно, модель для исходных данных записывается в виде

.

2.7. Вычисление по построенной модели прогнозных значений для моментов времени 25; 26.

2.8. Определение суммы квадратов отклонений прогнозных от фактических значений потребления яблок.

ВЫВОД ИТОГОВ 4.3.2.1
Регрессионная статистика
Множественный R	0,900037
R-квадрат	0,810067
Нормированный R-квадрат	0,801023
Стандартная ошибка	378,3206
Наблюдения	23
Дисперсионный анализ
	df	SS		MS		F		Значимость F
Регрессия	1	12819202		12819202		89,56557		5,04E-09
Остаток	21	3005655		143126,4
Итого	22	15824857
	Коэффициенты	Стандартная ошибка		t-статистика		P-Значение		Нижние 95%		Верхние 95%
Y-пересечение	683,5531	642,6216		1,063695		0,299546		-652,852		2019,958
Переменная X 1	0,919154	0,097122		9,463909		5,04E-09		0,717178		1,12113

2.9. Оформление полученных результатов в виде табл. 4.3.2.7.

Т а б л и ц а 4.3.2.7

25	7820	7674,30	21228,71
26	7730	7802,98	5326,19
			26554,91

2.10. Последовательное изменение параметра в интервале (0; 1) с шагом 0,1 и проведение всех расчетов п. 2.1-2.9. Оформление промежуточных результатов в виде табл. 4.3.2.8.

Т а б л и ц а 4.3.2.8

	0,1	0,2	0,3	0,4	0,5
	26554,9	43026,3	78931,6	117823	138404
	0,6	0,7	0,8	0,9
	551719	1261971	53245,1	25672,8

2.11. Уточнение параметра =0,90 с шагом 0,01 и проведение всех расчетов п. 2.1-2.9. Оформление промежуточных результатов в виде табл. 4.3.2.9.

Т а б л и ц а 4.3.2.9

	0,91	0,92	0,93	0,94	0,95	0,96
	25082,25	25048,00	25615,18	26830,12	28740,29	31393,99

Таким образом, оптимальным параметром является = 0,92.

3. Построение прогнозной модели с использованием оптимального параметра = 0,92 путем последовательного выполнения шагов 2.2. – 2.6 для . В результате получится модель, которая записывается в виде

.

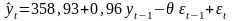4. Расчет по построенной модели прогнозных оценок потребления яблок на два года

,

.