Міністерство освіти україни донецький національний університет

Гаркуша В.В., Зюбанов О.Є., Пойманов В.Д.

Юрченко В.М.

Посібник для розв’язування задач з електродинаміки (постійні електричне та магнітне поля)

Рекомендовано до

видання рішенням ради

фізичного факультету ДонНУ

(протокол № від 2010р.)

Донецьк 2010

УДК 537(075.34)

Збірник задач з електродинаміки: Навчальний посібник / Гаркуша В.В., Зюбанов О.Є., Пойманов В.Д., Юрченко В.М. - Донецьк: ДонНУ, 2010. - 42с.

Зібрано задачі по наступним розділам електродинаміки : постійні електричне і магнітне поля. Перед кожною темою вміщено перелік основних теоретичних положень та формул. Збірник розрахований на студентів-фізиків, радіофізиків.

^{Рецензенти:}

д-р фіз.- мат наук, професор Любчанскій І.Л.

д-р фіз.- мат наук, с.н.с. Стефановіч Л.І.

Технічні редактори:

Передмова.

В даний збірник задач зібрано задачі, які на протязі останніх років розв’язувались на практичних заняттях при вивченні курсу електродинаміки студентами фізичного факультету. Для полегшення роботи студентів перед кожним розділом поміщено основні теоретичні відомості. До збірника включено найбільш характерні і типові задачі курсу електродинаміки по наступнім темам: постійні електричне та магнітне поля. Частина задач складена авторами, інші підібрані з різних збірників задач і відповідно перероблені. Всі задачі мають детальні розв’язки, тому даний збірник може використовуватись студентами для самостійної роботи.

Основні формули теорії.

В криволінійних ортогональних системах координат мають місце наступні тотожності:

в сферичній системі координат:

, , ;

, , ;

;

;

;

;

;

;

в циліндричній системі координат:

, , ;

, , ;

;

;

;

;

;

.

При любих і мають місце тотожності:

; ; .

Основні інтегральні теореми, які дозволяють перетворювати об’ємні, поверхневі і контурні інтеграли один в одного.

Теорема Остроградського-Гаусса:

,

де –деякий об’єм; - замкнута поверхня, яка обмежує цей об’єм.

Теорема Стокса:

де - замкнутий контур, - довільна поверхня, яка опирається на цей контур.

Напруженість електричного поля задовольняє рівнянням Максвелла:

; .

Електростатична теорема Гаусса:

.

Напруженість і потенціал електричного поля пов’язані співвідношенням:

.

Потенціал задовольняє рівнянню Пуассона:

.

На зарядженій поверхні, яка розділяє дві області 1 і 2

,

.

Нормаль направлена з області 1 в область 2, - поверхнева густина зарядів.

Енергія електростатичного поля

;

.

Рівняння Максвела мають вигляд

, ,

де - магнітна індукція, - напруженість магнітного поля, - густина об’ємного струму.

де - магнітна проникливість середовища.

Елемент струму створює в вакуумі, або однорідному середовищі створює магнітне поле

.

Граничні умови для векторів і на межі двох областей 1 і 2

, ,

де - нормаль до межі розділу областей, - густина поверхневого струму.

Магнітне поле можна задати за допомогою векторного потенціалу

.

З додатковою умовою

.

В однорідних магнетиках

.

Енергія магнітного поля, яка локалізована усередині об’єму V виражається

.

ЗАДАЧІ ТА ЇХ РОЗВ’ЯЗУВАННЯ.

1. Знайти за допомогою закону Кулона потенціал і напруженість поля в вакуумі, яке створюється нескінченною прямолінійною ниткою, рівномірно зарядженою з лінійною густиною .

Розв’язання. Виберемо елемент довжини нитки . Напруженість поля, яке створюється цим елементом: . Сумарна напруженість поля направлена перпендикулярно до нитки і по величині дорівнює :

2. Поле створюється в вакуумі рівномірно зарядженим колом радіусом R і зарядом Q. Знайти потенціал та напруженість поля на осі кола.

Розв’язання. Направимо вісь z вздовж вісі кола. Елемент довжини кола створить на осі z поле з напруженістю:

де .

Резельтуюча напруженість поля :

3. Потенціал поля в вакуумі

.

R₀ і a - постійні. R - відстань до вісі. Визначити відповідний розподіл зарядів.

Розв’язання. Напруженість електричного поля визначається:

Так як задача має циліндричну симетрію, то :

Із рівняння Максвела знайдемо :

Для : ;

Для :

З отриманих виразів видно, що поле створюється зарядами, рівномірно розподіленими ( ) по об’єму нескінченно довгого циліндра радіуса .

4. За допомогою рівняння Лапласа визначити потенціал поля, яке створюється в вакуумі рівномірно зарядженою нескінченно довгою поверхнею круглого циліндра радіуса R. Знайти напруженість цього поля.

Розв’язання. Задача має аксіальну симетрію. Тому рівняння Лапласа матиме вигляд:

Можливі дві разв’язки:

( );

( ).

Із граничних умов на поверхні циліндра і

Знайдемо константи і :

Напруженість електричного поля:

5. За допомогою рівняння Пуассона визначити потенціал та напруженість поля, яке створюється нескінченним плоским шаром товщиною _2a, який рівномірно заряджений з об’ємною густиною . Діелектрична проникливість . Навколишнє середовище – вакуум.

Розв’язання. Направимо вісь х перпендикулярно до шару, а початок координат розмістимо на середній площині. Тоді і рівняння Пуассона матиме вигляд:

Необхідно розглянути два випадки: всередині і зовні шару.

1. Всередині шару ( )

Не зменшуючи загальності задачі можна покласти . Площина є площина симетрії і при . Тому і .

2. Зовні шару:

а) при .

б) при

Константи інтегрування знаходимо із граничних умов:

і (при x=a);

і (при x=-a).

Звідси знаходимо:

; ; .

6. За допомогою рівняння Пуассона визначити потенціал та напруженість поля, яке створюється кулею радіусом R рівномірно зарядженою з об’ємною густиною . Діелектрична проникливість . Навколишнє середовище – вакуум.

Розв’язання. Початок системи координат помістимо в центрі кулі. Так як заряд розподілений симетрично відносно центру кулі, то вектор напруженості електричного поля в сферичній системи координат матиме лише радіальну компоненту E_r, яка залежить лише від радіус – вектора r. Проведемо сферичну поверхню S , радіусом r(r>a) і використаємо теорему Гауса:

Потенціал зовні кулі буде:

Покладемо при . Тоді С=0 і .

Дослідимо поле всередені кулі (r<a). Проведемо сферичну поверхню S₂ радіусом r<a. За теоремою Гауса:

; .

Позначимо об’ємну густину зарядів: .

Всередині поверхні S₂ буде заряд: , тому

На поверхні кулі

7. В однорідне електростатичне поле з напруженістю внесли металеву кулю радіусом R. Діелектрична проникливість середовища .

Розв’язання. Початок системи координат помістимо в цент кулі. Так як куля металева, то напруженість поля всередині кулі дорівнює нулю. Зовні кулі поле описується зівнянням Лапласа. Розмістемо екваторіальну площину перпендикулярно вектору ₀.так як поле симетричне, то напруженість і потенціал поля будуть залежати лише від двох сферичних координат r і .

Рівняння Лапласа в сферичній системі координат має вигляд:

(1).

Розв’язок цього рівняння будемо шукати у вигляді добутку двох функцій, одна з яких залежить від координати r, а друга від координати .

(2).

Підставимо в рівняння (1), отримаємо:

(3).

Домножимо обидві частини рівності на , отримаємо:

(4).

Ця рівність мусить виконуватись при довільних значеннях і .це можливо лише в тому випадку, коли кожна із частин рівняння дорівнює постіній величині р²:

(5).

(6).

Розв’язком рівняння (5) є . Після підстановки f₂ в (5) отримаємо, що . Рівняння (6) тепер матиме вигляд:

(7).

Введемо нову змінну таким чином, щоб:

.

Тоді:

Підставимо ці похідні у рівняння (7), отримаємо:

Загальний інтеграл цього рівняння: .

Корені харастеристичного рівняння дорівнють , .

Тоді .

Для потенціалу отримаємо: .

Знайдемо напруженість поля:

, де

, , .

Для визначення постійних інтегрування використаємо граничні умови. При куля не впливає на поле, тому , , .

Поверхня кулі являється еквіпотенціальною. Тому при для всіх значень .а це можливо при умові .

Звідси .

Підставимо значення і ,отримаємо:

Найбільша напруженість поля буде в точці , .

.

8. Два однакових та протилежних по знаку точкових зарядів +q і –q розміщені на кулях з провідника з радіусами R₁ і R₂ відповідно. Відстань між кулями 2h ( , ). Знайти потенційні коефіцієнти та ємність системи.

Розв’язання. Так як і , то електричні центри співпадають з геометричними центрами. Потенційний кщефіцієнт дорівнює потенціалу першого провідника, коли його заряд дорівнює одиниці, а заряд другого доівнює нулю. дорівнює потенціалу першого провідника, коли заряд другого провідника дорівнює одиниці, а першого (і усіх інших) дорівнює нулю.

, .

Аналогічно: , .

Потенціали провідників:

Емкість системи: .

9. В однорідне магнітне поле з напруженістю внесли круглий прямий циліндр з радіусом так, що його вісь перпендикулярна вектору . Магнітна проникливість матеріалу циліндра , навколишнього середовища . Визначити поле всередині та зовні циліндра. Крайові ефекти не враховувати.

Розв’язання. Вісь циліндричної системи координат виберимо так, щоб вона співпадала з віссю циліндра. Будемо вважати, що вектори поля не залежать від координати z. Скалярний потенціал задовольняє рівнянню:

, (1)

і в циліндричній системі координат матиме вигляд:

, (2).

Розв’язок будемо шукати у вигляді добутку двох функцій:

, (3).

Підставимо в рівняння (2), отримаємо:

, (4).

Розділимо всі члени рівняння на і домножимо на . Будемо мати:

, (5).

Так як ця рівність справедлива при довільних значеннях і , права і ліви частини мусять бути рівними деякій константі, яку ми позначимо через . Отримаємо два рівняння:

, (6).

, (7).

Розв’язком рівняння (6) буде:

.

Із умов симетрії при заміні на функція знаку не змінює. Тому .

Оскільки магнітний потенціал не може мати функцій, які кратні куту то . Отже .

Із рівняння (7) знайдемо:

.

В середині циліндра будемо мати:

, (8)

; .

Зовні циліндра:

, (9).

Напруженість магнітного поля будемо шукати так: .

Так як при напруженість магнітного поля скінченна, то . При впливом циліндра можна знехтувати, тому , або

, .

При : , або

, .

Із непреривності потенціалу випливає, що при :

, або .

Підставимо значення К₁:

Для поля в середині циліндра маємо

Модуль вектору , , не змінить від положеня точки в середині циліндра.

Напрудженість зовнішнього магнітного поля

10. Площина XY несе заряд з періодичною поверхневою густиною . Знайти потенціал єлектричного поля в необмеженому просторі.

Розв’язання. Позначимо при а при Потенціали задовільняють рівнянням

(1) и (2)

На площині XY виконуються граничні умови

При , тому, що повний заряд на площині равен 0.

Оскільки функція cos (...) оператором Лапласа відтворюється, то розвязки будемо шукати у вигляді:

Підставимо і у рівнання (1) і (2)

(3)

(4)

Із умови, що і при маємо

С₁ і С₂ находим із граничних умов:

11. Плоский конденсатор у якого відстань між обкладками d, різниця потенціалів на них , вертикально занурили в рідкий діелектрик. На яку висоту підійметься діелектрик між пластинами? Капілярністю знехтувати.

Розв’язання. Позначемо ємність конденсатора до занурення в діелектрік через С₁, а після занурення через С₂. Тоді

де а – шириа конденсатора,

в – висота конденсатора,

х – відстань, на яку його занурили в діелектрік.

Енергія конденсатора збільшиться на величину:

На діелектрік з боку електричного поля конденсатора буде діяти сила:

Ця сила врівноважується вагою діелектрика Звідки

12. Знайти енергію і силу взаємодії двох паралельних нескінченних ниток, рівномірно заряджених з лінійними густинами  та  і розташованих на відстані одна від одної в однорідному середовищі з діелектричною проникливістю .

Розв’язання. Енергія одиниці довжини однієї нитки в колі іншої . Потенціал поля другої нитки . Тому .

Сила, яка діє на одиницю довжини нитки

13. Визначити силу взаємодії ниток з попередньої задачі за допомогою максвелівського тензора натягу.

Розв’язання. Розглянемо , площину, яка проходить через середину відрізка, який з’єднує нитки, перпендикулярно до нього.

На одиницю довжини (вздовж ниток) цієї площини припадає сила

. Тоді

14. Знайти потенціал та напруженість електричного поля кулі , яка рівномірно заряджена по об’єму. Радіус кулі R, заряд q. Діелектрична проникливість навколишнього середовища . За допомогою рівняння Пуассона знайти потенціал і напруженість поля зовні і в середині рівномірно заряженої з густиною кулі.

Розв’язання. Потенціал рівномірно заряженої кулі має сферичну симетрію і заменіть лише від відстані r від центру кулі. Виберемо сферичну систему координат з початком в центрі кулі. В середині кулі r a отримаємо рівняння Пуасона

(1)

Для області зовні кулі

(2)

Із цього рівняння, враховуючи, що при маємо Із (1) отримаємо

При R=0 потенціал , тому С₄ = 0. Із гранічних умов при R = a

і отримаємо рівняння для знаходження С₁ і С₃

.

Для потенціалів отримаємо вирази

Напружності полів дорівнюють

(r a)

(r a)

15. Знайти власну енергію кулі з радіусом а яка рівномірно заряжена по об’єму з густиною .

Розв’язання. Виберемо за елемент об’єм c . Енергія знаходиться по формулі:

Використаємо вираз для потенціалу кулі (задача №...), тоді

де - повний заряд кулі.

16. Визначити власну енергію сфери з зарядом q, рівномірно розподіленим по її поверхні, з густиною .

Розв’язання. Енергію сфери можна знайти за допомогою виразу

.

Потенціал сфери Тоді

17. Визначити взаємну енергію двох точкових диполів, які знаходяться на відстані r один від одного.

Розв’язання. Дипольний потенціал де - дипольний момент системи. Енергія одного диполя в полі іншого дорівнює

, де

18. Визначити векторний потенціал однорідного магнітного поля ( )

Розв’язання. Розглянемо то можна взяти

Тоді а

19. Визначити векторний потенціал і напруженість магнітного поля всередині і зовні нескінченного прямолінійного циліндра радіусом а. По циліндру тече струм з густиною

Розв’язання. Векторний потенціал задовольняє рівнянню

(1)

В циліндрічній системі координат це рівняння матиме вигляд

Поле циліндричного однорідного струму має циліндричну симетрію і тому векторний потенціал матиме лише компоненту A_z 0, яка залежить від координати r.

Тому - середині циліндра

і - зовні.

Розв’язками для внутрішньої і зовнішньої областей будуть

На вісі струму (r = 0) потенціал мусить бути скінченним, тому С₁ = 0. Так як циліндр нескінченний, то не можна вважати, що при . Використовуючи цумову непреревності

і при r = a, отримаємо

Величина С₄ не суттєва. Знайдемо напружність полів

20. Визначити векторний потенціал магнітного поля, яке створюється в вакуумі прямолінійним струмом I довжиною . Розглянути випадок, коли →∞.

Розв’язання. Виберемо початок координат в центрі відрізка, а вісь z направимо вздовж відрізка.

В точці Р(r,z) векторний потенціал розрахуємо згідно з формулою.

21. Диск радіусом рівномірно заряджений по поверхні з густиною . Знайти потенціал і напруженість електричного поля на вісі диску на відстані .

Розв’язання. За елемент площі виберемо кільце

По одну сторону від диску потенціал буде дорівнювати

Поле по нормалі дорівнює

По іншу сторону від диску х<0 і тому

22. Визачити потенціал і еквіпотенціальні поверхні заряда , який рівномірно розподілений вздовж відрізку довжиною з лінійною густиною.

Розв’язання. Задача має вісьову симметрію, тому достатньо розглянути поле в площині, яка проходить через вісь х, (на якій лежить відрізок 2l). В точці А(х,у) потенціал знайдемо таким чином

За допомогою підстановки інтеграл зводиться до елементарного і ми отримаємо

Лінії постійного потенціалу визначаються рівнянням

Позначимо через і відстані від кінців відрізка і до т. А, а через і - координати проекцій і на вісь х. Тоді

Це видно з того, що . Маємо два рівняння: і .

Складаємо ці рівняння і, враховуючи що отримаємо

Отже точки лежать на еліпсі з великою напіввіссю і лінійним ексцентриситетом .

23. Визначити ємність еліпсоїда обертання з напівосями .

Розв’язання. З попередньої задачі маємо

,

, а з іншого боку

Тому

24. Визначити ємність циліндричного провода довжиною . Радіус провода .

Розв’язання. Циліндричний провідник можна розглядати як еліпсоїд обертання, для якого . Тоді

25. Визначити силу, з якою притягуються обкладенки плоского конденсатора.

Розв’язання. позначимо через відстань між обкладинками. Тоді енергія дорівнює

де напруженість поля між обкладинками. Знак “-” означає, що сила намагається зменьшити відстань . На одиницю площаді діє сила .

26. Знайти напруженість магнітного поля на вісі круглого одношарового соленоїду довжиною і “витків” на одиницю довжини.

Розв’язання. Із точки зовні соленоїда переріз видно під тілесним кутом

Магнітний потенціал дорівнює

Магнітне поле вісі соленоїда знайдемо як

Аналогічно розраховується поле в середені соленоїда. В цьому випадку точка лежить на відстані від лівого кінця соленоїда і ділить його на дві частини.

Ліва частина створює потенціал, який можна отримати із виразу для , якщо покласти і замінити через :

Права частина створює від’ємний потенціал (тому що ), який знаходиться так само, якщо взяти і замінити через довжину правої частини :

Потенціал в середені соленоїда дорівнює

Напружність магнітного поля:

Якщо соленоїд нескінченний, то і напружність поля в середені соленоїда дорівнює

,

27. Визначити коефіцієнт самоіндукції відрізку довжиною L лінійного провідника радіусом a (a<<L) , по якому протікає струм силою I.

Розв’язання. Прямолінійний провідник довжиною L можна розглядати як частину замкнутого провідника зі струмом . На відстанях r L магнітне поле складає пропорційно . Тому енергією поля на таких відстанях можна знехтувати  На відстанях r<L поле прямолінійного провідника дорівнює H= : Магнітна енергія розраховується за формулою

ln

Магнітну енергію в серелині првідника можна не враховувати  Як відомо

Тому

28 Знайти силу взаємодії в повітрі між двома паралельними нескінченними прямолінійними струмами силою і . Відстань між ними 2a.

Розв’язання. Напруженість магнітного поля створюваного струмом в місці знаходження струму

На основі формули

де - сила яка діє на елемент лінійного струму в зовнішньому полі отримаємо що на кожну одиницю довжини одного струму діє з боку другого струму сила

Для паралельних струмів ця сила має характер притягування  для антипаралельних відштовхування

9. Розв’язати попередню задачу за допомогою тензора натягу Максвела.

Розв’язання. Виберемо площину в якій лежать струми за координатну площину XZ і вісь X направимо перпендикулярно струмам Сила  яка діє на одиницю довжини першого струму розраховується з допомогою максвеловського тензора натягу наступним чином

Напруженість поля створюваного струмом I₁ має компоненти

Аналогічно розраховуються і компоненти напруженості поля створюваного струмом I₂

Після інтегрування отримаємо :

;

30. Плоский контур обертається кутовою швидкістю в однорідному магнітному полі навколо вісі, яка перпендикулярна полю. Індукція поля . Визначити електрорушійну силу в контурі. Площа контуру . Визначити силу струму в контурі, cамоіндукція контуру , опір .

Розв’язання. Ерс індукції розраховується за формулою

де =кут між нормаллю до контура і напрямком поля в початковий момент часу t=0 

Сила струму в контурі буде визначатись диференціальним івнянням



Після інтегрування отримаємо

де , - постійна інтегрування, яка залежить від початкової сили струму.

31. Заряджений конденсатор з ємністю замкнутий на опір з самоіндукцією . Визначити заряд на обкладках конденсатора як функцію часу. Початковий заряд .

Розв’язання. Так як різниця потенціалів на обкладинках конденсатора дорівнює , то аналогічно попередній задачі маємо

Сила струму в контурі :

Підставимо в попереднє рівняння і отримаємо

Загальний розв’язок цього рівняння запишемо у вигляді

,

де ; ;

Враховуючи початкові умови (при , , )

;

32. Вивести рівняння для напруженості магнітного поля і векторного потенціалу в коаксіальному кабелі шляхом інтегрування рівнянь Пуассона–Лапласа для векторного потенціалу. Радіус внутрішнього провідника , зовнішнього і відповідно ( ).

Розв’язання. Виберемо ціліндричну систему координат. Так як вектор густини струму має лише одну проекцію, то і векторний потенціал теж матиме лише одну проекцію на вісь , яка перпендикулярна площини малюнка. Всередені центрального провідника ( ) рівняння Пуассона матиме вигляд:

де - магнітна проникність матеріалу провідника. Після інтегрування отримаємо

Розрахуємо напружність магнітного поля

Враховуючи, що , , запишемо вириз для ротора в ціліндричній системі координат

Оскільки скінченна величина при , то теж можна вибрати 0.

;

Між провідниками ( ) густина струму дорівнює нулю, тому зідно з рівнянням Лапласа матимемо:

Після інтегрування отримаємо

, ;

Для знаходження постійних інтегрування використаємо граничні умови при :

Векторний потенціал неперервний, тому при

;

В товщі труби ( ) густина струма постійна і дорівнює

Рівняння Пуассона матиме вигляд

Після інтегрування отримаємо

Постійні і визначимо з граничних умов. При : ,

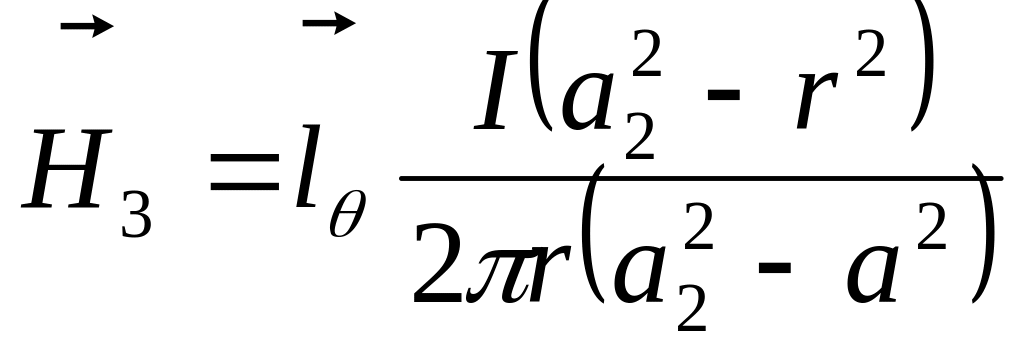
Зовні кабелю векторний потенціал постійний

33. По двох паралельних стрічкових провідниках в протилежних напрямках течуть однакові постійні струми Ширина і довжина провідників не обмежена товщина мала  Один з провідників розташований в площині X0Z інший на відстані 2с від ней  Напрямок струмів паралельний вісі XВизначити потенціал і напруженість магнітного поля в точках 0  якщо поверхнева густина струму 

Розв’язання. Виділимо в лівому провіднику нитку струму дуже малой ширини dz  на відстані Z від вісі X паралельно до неї  Величина струму в цій нитці  Цей струм створює в деякій точці m на відстані y від силового провідника з напруженістю dH Розкладемо ії на дві складові такої ж величини  але протилежного напрямку  яка створюється струмом в другій нитці струму  на відстані Z від вісі X

Компонента



Замінимо ; = ;

Тоді

Проінтегруємо по всій нескінченній ширині лівого провідника  що відповідає зміні кутової змінної інтегрування від до 



Внаслідок симетрії в точці m правий провідник створює поле з такою ж самою напруженістю  Повна напруженість



Таке поле називається однородним

Векторний потенціал прямої нитки струму паралельний до неї в просторі між провідниками матиме лише одну складову



Запишемо компоненти ротора і прирівняємо їх величини  Отримаємо





Виберемо при y=c Отримаємо



Таким чином 

34. По прямому круглому циліндричному провіднику радіуса a тече струм з постійною густиною  В провіднику є циліндрична порожнина з круглим перерізом і радіусом b<a. Вісі обох циліндрів і паралельні і розташовані на відстані с одна від одної Знайти напруженість поля в пустоті  якщо магнітна проникливість матеріалу провідника і середовища  яке заповнює порожнину  однакова і дорівнює 

Розв’язання. Виберемо напрям струму вздовж вісі Z Вісь X проведемо через т і  Якби порожнини не було  то напруженість в точці p дорівнювала б

; 

В порожнині струму немає  Але можна вважати що в ній є два уявних протилежно напрямлених однакових по величині струми Напруженість поля в точці p від уявного струму  який тече в напрямку  протилежному струму провідника :



Загальна напруженість вточці р

Але

Тому 

Магнітне поле в порожнині однорідне  Вектор перпендикулирний прямій  а



35. Знайти потенціал електричного поля еліпсоїда виготовленого з провідника 

Розв’язання. Нехай - деяка функція  яка задається рівнінням

(1)

( >0) Рівняння задає сімейство сфокусованих поверхонь другого порядку При це сімейство еліпсоїдів; при – однополосних гіперболоїдів; при - двополосних гіперболоїдів В усіх випадках рівняння може бути сімейством еквіпотенціальних поверхонь  Для цього необхідно виконання умови:

(2)

Введемо функцію

(3)

Продиференцюємо рівняння (1) по x

Звідсі



Подвійне диференцювання дасть:



Напишемо аналогічні похідні по y i z і складемо їх  Після спрощення отримаємо :

(4)

Отже умова (2) виконується і

(5)

Задача зводиться до інтегрування рівняння

(6)

Якщо всі знайменники в правій частині рівняння (6) будуть додатні  то еквіпотенціальними поверхнями (1) будуть софокусні еліпсоїди  При =0 отримаємо еліпсоїд

(7)

Якщо потенціал знайти з рівняння (6) то на поверхні еліпсоїдів (7) він буде постійним і буде розв’язком даної задачі Проінтегруємо рівняння(6) отримаємо :

(8)

де А- постійна інтегрування 

Виберемо потенціал для нескінченно віддаленої точки і проінтегруємо ще раз

(9)

Постійна А визначається з умови що на великих відстанях потенціал переходить в потенціал точкового заряду

При великих значеннях еліпсоїд (1) переходить в кулю з радіусом  а інтеграл (9) в

Отже (10)

Це еліптичний інтеграл  Для витягнутого еліпсоїда обертання (b=c)

(11)

Нехай

Тоді

(12)

Величина 2А це велика вісь еквіпотенціального еліпсохда  2f = відстань між фокусами

Сімейства софокусних еліпсоїдів 

Для стиснутого еліпсоїда (a=b)

- це мала вісь еліпсоїда  а

- відстань між фокусами

36. Знайти емкість одиниці довжини двох парадедьних нескінченно довгих циліндрів з радіусами a і b  Відстань між вісями ціліндрів l

Розв’язання. Візьмемо дві нескінченно довгі паралельни прямі і  рівномірно заряжені з зарядами протилежних знаків (мал)  Еквіпотенціальними поверхнями будуть круглі циліндри  Нехай і два з них  розташовані зовні один від одного  Розташування вісей циліндрів задано умовою

Потенціали поверхностей S і S’ будуть

(1)

де

Якщо заряди і перейдуть з ліній і на поверхні цидіндрів S і S’  то поле всередині циліндрів перетвориться в нуль  а в зовнішньому просторі не зміниться  Отримаємо необхідний для задачі розподіл зарядів  Знайдемо і ємкість

(2)

Для визначення d і d’ маємо рівняння



з яких знаходимо

Розглянемо випадок  коли циліндр S’ повністю лежить всередині циліндра S  Розмірковуючи аналогічно отримаємо

37. Два однакових контура і мають форму квадратів із стороною а  Сторони квадратів паралельні  а їхні центри лежать на відстані d від прямої  яка перпендикулярна їх площинам  Визначити коефіцієнт взаємної індукції цих квадратів і силу  з якою притягуються контури  якщо по ним течуть струми і 

Розв’язання. Коефіцієнт взаємної індукції визначається за формулою

Всі члени що відносяться до взаємно перпендикулярних пар елементів і  дорівнюють нулю Для двох паралельних прямих довжиною a на відстані h одна від одної маємо (мал)

де і координати точок обох відрізків 

Після інтегрування отримаємо

Комбінуючи попарно паралельні сторони квадратів і отримаємо чотири пари відрізків  для яких h=d  і чотири пари  для яких По перших чотирьох парах течуть паралельні струми  а по інших чотирьох протилежні  Таким чином



Для визначення сили притягання між квадратами використаємо формулу

