МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ
ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
Гаркуша В.В., Зюбанов О.Є.,
Пойманов В.Д., Юрченко В.М.
ПОСІБНИК ДЛЯ РОЗВ’ЯЗУВАННЯ
ЗАДАЧ З ЕЛЕКТРОДИНАМІКИ
(основи векторного і тензорного аналізу, спеціальна теорія відносності та релятивістська механіка)
Рекомендовано до
видання рішенням ради
фізичного факультету ДонНУ
(протокол № від 27.06.2010 р.)
Донецьк 2010
УДК 53(075.34)
Збірник задач з електродинаміки: Навчальний посібник / Гаркуша В.В., Зюбанов О.Є., Пойманов В.Д., Юрченко В.М. -Донецьк: ДонНУ, 2010.-51с.
Зібрано задачі по спеціальній теорії відносності та основами векторного і тензорного аналізу. Перед кожною темою вміщено перелік основних теоретичних положень та формул. Збірник розрахований на студентів-фізиків, радіофізиків.
Рецензенти:
д-р фіз.- мат наук, професор Любчанскій І.Л.
д-р фіз.- мат наук, с.н.с. Стефановіч Л.І.
Технічні редактори:
Передмова.
В даний збірник задач зібрано задачі, які на протязі останніх років розв’язувались на практичних заняттях при вивченні курсу електродинаміки студентами фізичного факультету. До збірника включено найбільш характерні і типові задачі курсу електродинаміки. Частина задач складена авторами, інші підібрані з різних збірників задач і відповідно перероблені. Всі задачі мають детальні розв’язки, тому даний збірник може бути рекомендований для самостійної роботи студентів. В даний збірник включено наступні розділи: основи векторного і тензорного аналізу, спеціальна теорія відносності та релятивістська механіка.
Основи векторного і тензорного аналізу.
В криволінійних ортогональних системах координат мають місце наступні тотожності:
в сферичній системі координат:
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
в циліндричній системі координат:
![]() ,
,
![]() ,
,
![]() ;
;
,
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
При
любих
![]() і
і
![]() мають місце тотожності:
мають місце тотожності:
;
![]() ;
;
![]() .
.
Основні інтегральні теореми, які дозволяють перетворювати об’ємні, поверхневі і контурні інтеграли один в одного.
Теорема Остроградського-Гаусса:
![]() ,
,
де
![]() –деякий
об’єм;
–деякий
об’єм;
![]() -
замкнута поверхня, яка обмежує цей
об’єм.
-
замкнута поверхня, яка обмежує цей
об’єм.
Теорема Стокса:
![]()
де
![]() -
замкнутий контур,
-
довільна поверхня, яка опирається на
цей контур.
-
замкнутий контур,
-
довільна поверхня, яка опирається на
цей контур.
Задачі та їх розв’язання.
Два напрямки
 і
і
 в
сферичній системі координат визначаються
кутами
в
сферичній системі координат визначаються
кутами
 ,
, і
і
 ,
,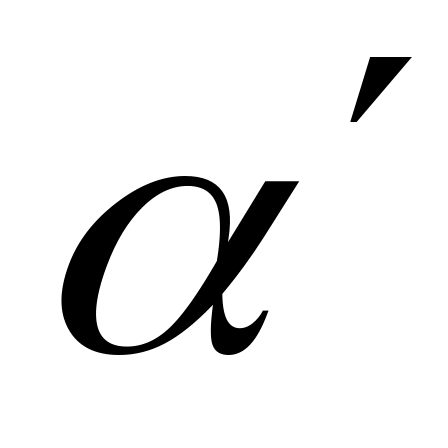 .
Знайти косинус кута між ними.
.
Знайти косинус кута між ними.
Р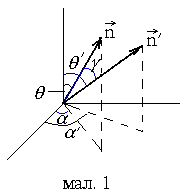 озв’язання.
Так як
і
- одиничні вектори, то їх скалярний
добуток дорівнює:
озв’язання.
Так як
і
- одиничні вектори, то їх скалярний
добуток дорівнює:![]() .
.
З другого боку:
![]() .
.
З мал.1. видно, що:
мал.1. видно, що:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
З
цих рівнянь можна знайти
![]() :
:
![]()
Довести, що коли
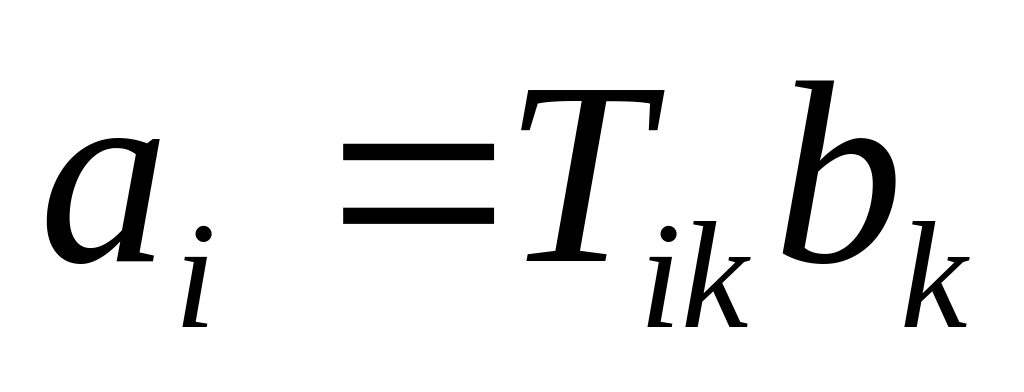 в кожній системі координат і
в кожній системі координат і
 -
тензор другого
рангу, а
-
тензор другого
рангу, а
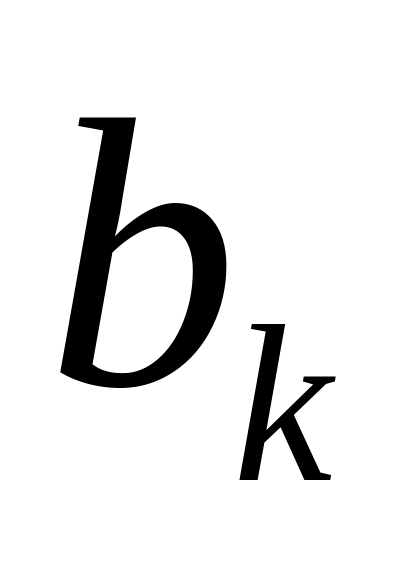 -
вектор, то
-
вектор, то
 -
також вектор.
-
також вектор.
Розв’язання.
В іншій
системі координат цей вираз має вигляд
![]() .
.
Компоненти
тензора
![]() і вектора
і вектора
![]() виражаються через
виражаються через
![]() і
і
![]() в силу їх тензорних і векторних
властивостей:
в силу їх тензорних і векторних
властивостей:
![]() ;
;
![]() .
.
Використовуючи ці формули знаходимо:
![]() .
.
Таким
чином компоненти величини
![]() при зміні системи координат перетворюються
як компоненти вектора.
при зміні системи координат перетворюються
як компоненти вектора.
Показати, що компоненти тензора
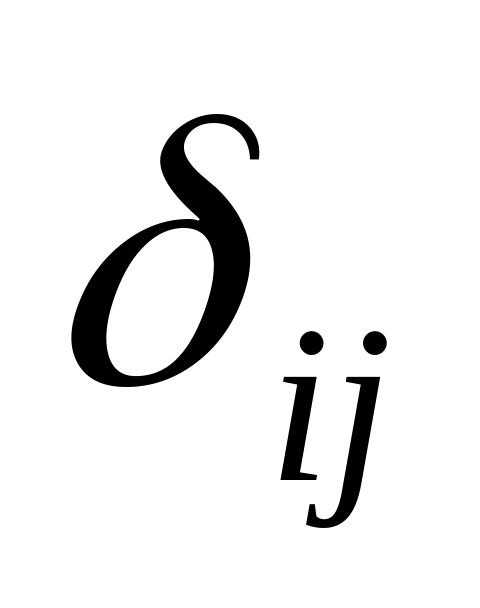 (символ Кронекера) являється тензором
другого рангу.
(символ Кронекера) являється тензором
другого рангу.
Розв’язання. Якщо - тензор другого рангу, то мусить виконуватись рівність:
![]() .
.
Так
як
![]()
![]()
![]() .
.
Таким
чином, компоненти тензора
![]() інваріантні відносно всіх систем
координат.
інваріантні відносно всіх систем
координат.
Довести, що величина
 є тензором другого рангу.
є тензором другого рангу.
Розв’язання. Виконаємо наступні перетворення
![]() .
.
Так
як
![]() і
і
![]() є компонентами векторів:
є компонентами векторів:
![]() ,
,
![]() .
.
Тоді отримаємо:
![]() .
.
Ми отримали закон перетворення компонентів тензора другого рангу.
Довести, що властивість симетрії (антисиметрії) тензора зберігається при поворотах системи координат.
Розв’язання.
При умові
![]() (симетричний тензор другого рангу).
Покажемо, що і в новій системі координат
(симетричний тензор другого рангу).
Покажемо, що і в новій системі координат
![]() .
Використаємо тензорні властивості:
.
Використаємо тензорні властивості:
![]() .
.
Довести, що коли тензор
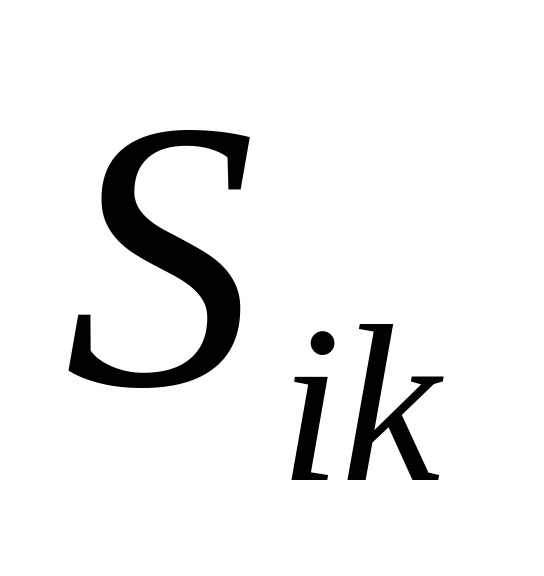 -
симетричний, а тензор
-
симетричний, а тензор
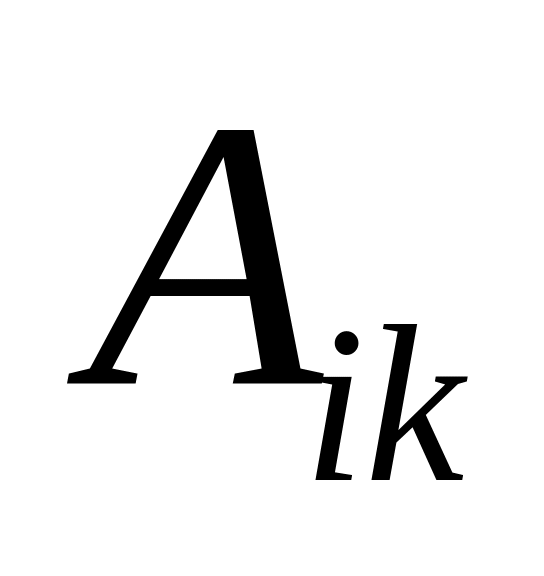 -
антисиметричний, то
-
антисиметричний, то
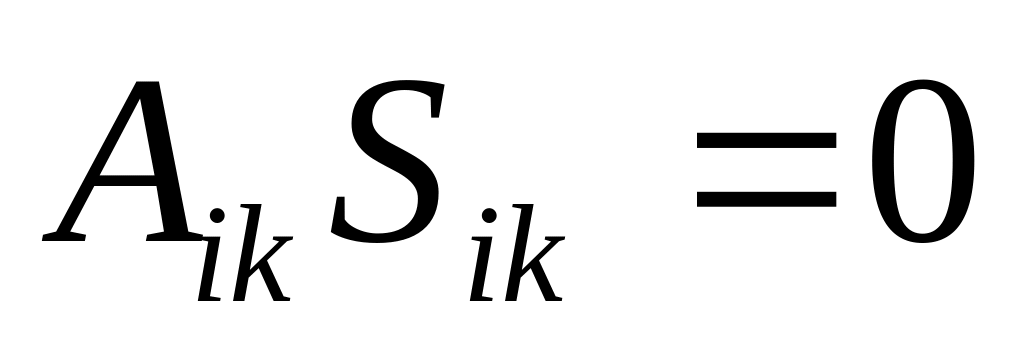 .
.
Розв’язання.
По умові
![]() ,
,
![]()
![]()
Довести, що сума діагональних компонент тензора другого рангу є інваріантом.
Розв’язання.
Знайдемо
суму діагональних компонент тензора
![]() в іншій системі координат
в іншій системі координат
![]()
Нехай у всіх системах координат компоненти вектора
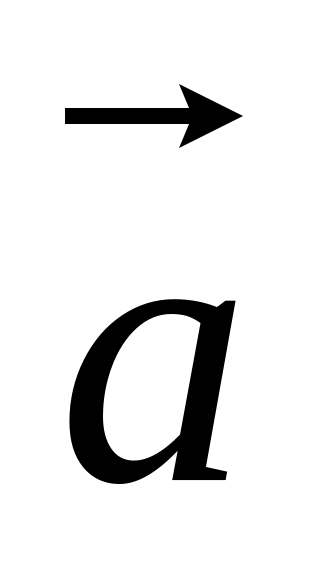 лінійно виражаються через компоненти
вектора
лінійно виражаються через компоненти
вектора
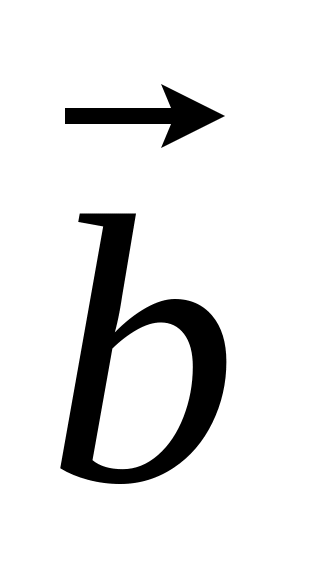 :
:
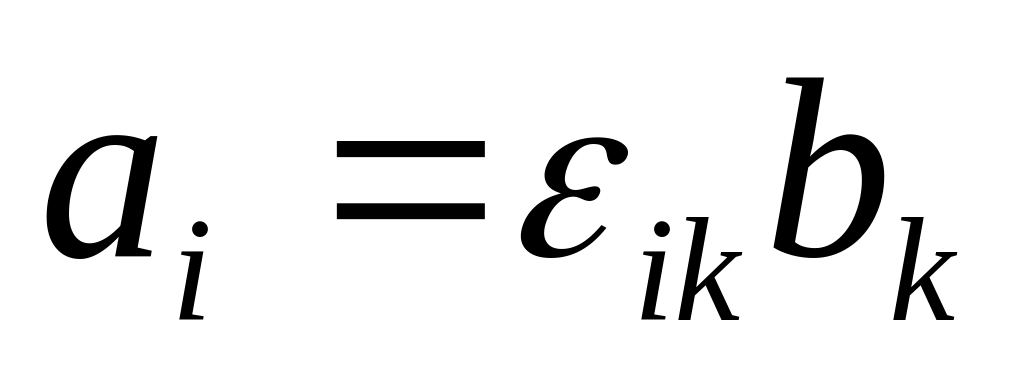 .
Довести, що сукупність величин
.
Довести, що сукупність величин
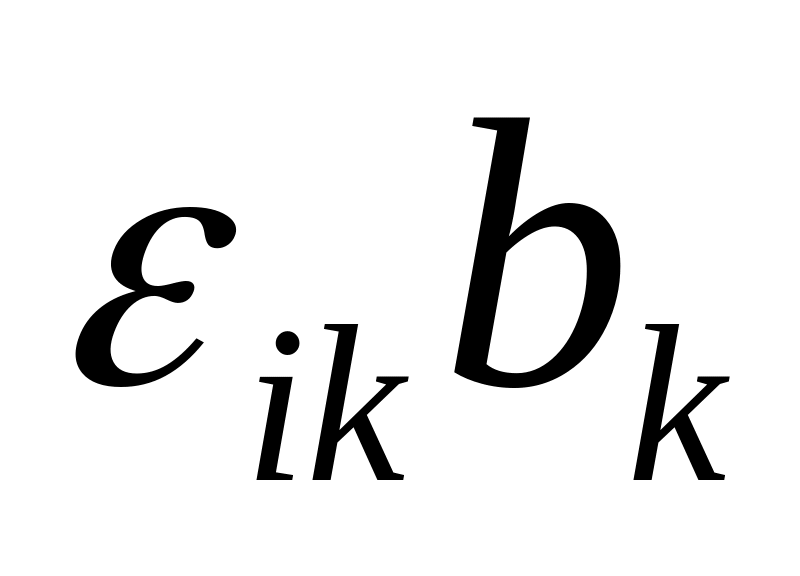 є тензором другого рангу.
є тензором другого рангу.
Розв’язання.
По умові
![]() ,
,
![]() .
.
Використаємо наступні рівності:
,
![]() ,
,
![]() .
.
Помножимо
останню рівність на
![]() і використаємо властивість матриць
:
і використаємо властивість матриць
:
![]() ;
тоді
;
тоді
![]() .
.
Можна
записати, що
![]() і скоротимо на
і скоротимо на
![]() .
Отримаємо
.
Отримаємо
![]() .
.
Це і є закон перетворення компонент тензора
Довести, що сукупність величин
 ,
де
,
де
 -
тензор третього рангу, а
-
тензор третього рангу, а
 -
тензор другого рангу, являється вектором.
-
тензор другого рангу, являється вектором.
Розв’язання. Запишемо цей вираз в нових координатах:
![]()
Показати, що матриця нескінченно малого повороту системи координат ε може бути записана у вигляді ε=I+ε1, де ε1 - антисиметрична матриця (
 ).
).
Розв’язання.
Розглянемо
довільний вектор
![]() в двох системах координат, які можна
сумістити нескінченно малим поворотом.
Матрицю такого перетворення представимо
у вигляді
в двох системах координат, які можна
сумістити нескінченно малим поворотом.
Матрицю такого перетворення представимо
у вигляді
![]() і покажемо, що
і покажемо, що
![]() .
.
Довжина
в обох системах координат однакова
![]() .
.
![]() .
.
Ми
використали властивість
![]() .
.
Звідси
випливає, що
![]() тобто
,
оскільки
тобто
,
оскільки
![]() є інваріантна величина.
є інваріантна величина.
Довести, що коли
 - ортогональна матриця перетворення,
то при її транспонуванні отримаємо
матрицю оберненого перетворювання.
- ортогональна матриця перетворення,
то при її транспонуванні отримаємо
матрицю оберненого перетворювання.
Розв’язання. Розглянемо довільний вектор в двох ортонормованих базисах, які пов’язані між собою співвідношеннями:
![]() ;
;
![]() ;
;
![]() .
.
Розкладемо вектор по цим базисам:
![]() ;
;
![]() .
.
Прирівняємо праві частини
![]() .
.
Помножимо
цю рівність скалярно на
![]()
![]() ,
,
![]() ,
,
![]() .
.
Якщо
попередню рівність помножити на
![]() ,
то отримаємо
,
то отримаємо
![]() .
.
З цих рівностей і випливає твердження задачі.
Знайти рівняння лінії вектора
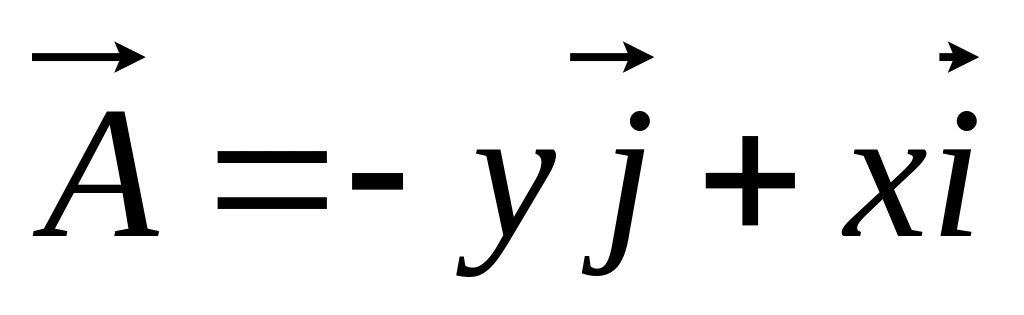 .
.
Розв’язання.
Поле плоске у всіх площинах
![]() ,тому лінії вектора
,тому лінії вектора
![]() будуть однакові. Вони визначаються із
співвідношення:
будуть однакові. Вони визначаються із
співвідношення:
![]() .
.
Так
як
![]() ;
;
![]() ,
то
,
то
![]() .
.
Після інтегрування отримаємо
![]() .
.
Покладаємо
![]() .
Тоді рівняння лінії вектора матиме
вигляд
.
Тоді рівняння лінії вектора матиме
вигляд
![]() для
всіх
.
Це сім’я кіл з радіусами
для
всіх
.
Це сім’я кіл з радіусами![]() .
Вони лежать в площинах, паралельних
площині x0y.
Їх центри лежать на вісі z.
.
Вони лежать в площинах, паралельних
площині x0y.
Їх центри лежать на вісі z.
Підрахувати потік вектора
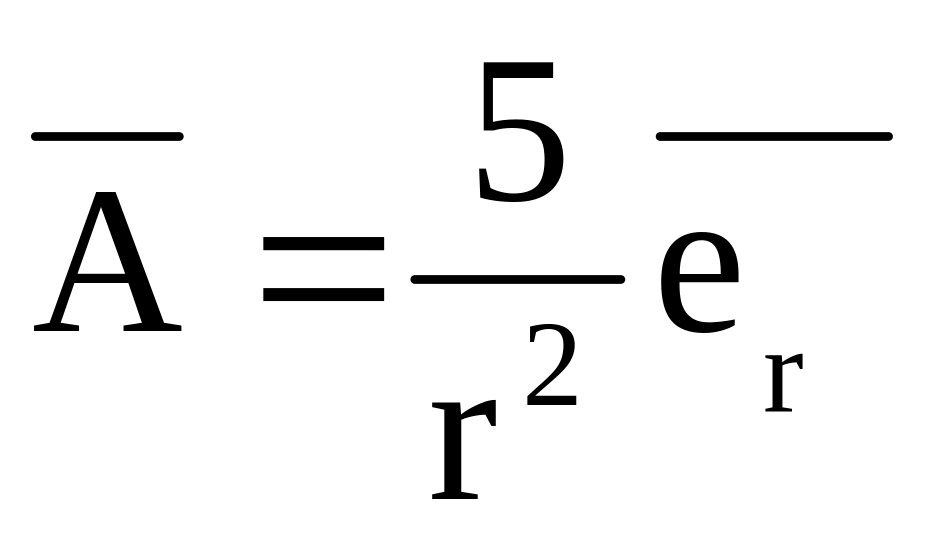 через сферичну поверхню радіусом
через сферичну поверхню радіусом
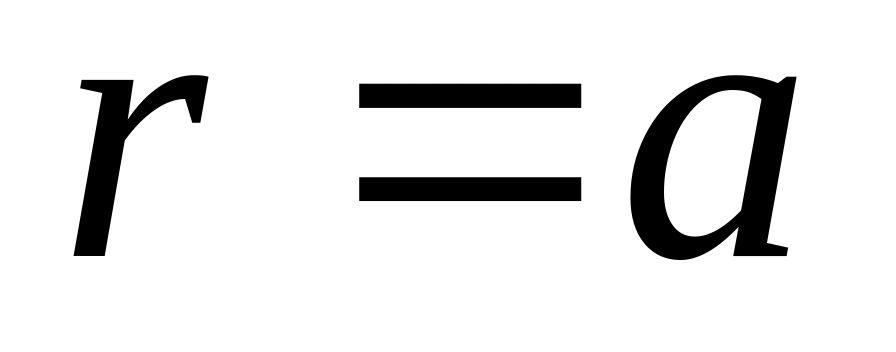 .
Центр сфери співпадає з точкою
.
Центр сфери співпадає з точкою
 .
.
Розв’язання. Потоком вектора через замкнуту поверхню називають скалярну величину
![]() ,
,
де
![]() -
проекція вектора на напрям додаткової
нормалі до площадки. Так як у задачі
поверхня S-
сферична і напрям вектора
співпадає з напрямком радіус-вектора,
то
-
проекція вектора на напрям додаткової
нормалі до площадки. Так як у задачі
поверхня S-
сферична і напрям вектора
співпадає з напрямком радіус-вектора,
то
![]() для всіх точок поверхні інтегрування.
для всіх точок поверхні інтегрування.
Отже потік буде
![]() .
.
Обчислити дивергенцію радіус-вектора прямокутній декартовій, сферичній, та циліндричній системах координат.
Розв’язання. В декартовій системі координат
![]() ,
,
де
вектор
має компоненти
![]()
В
сферичній системі координат вектор
має компоненти
![]() ,
тому
,
тому
![]() .
.
В
циліндричній системі координат
![]() .
.
![]() .
.
Довести наступні тотожності:
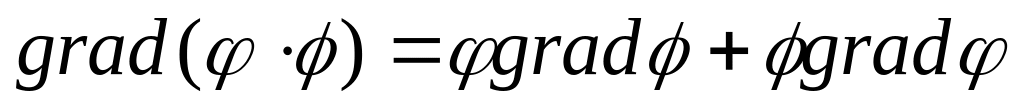 ;
; ;
; ;
; .
.
Розв’язання. 1) Запишемо i-ту компоненту вектора в лівій частині:
![]() .
.
Із рівності проекцій векторів в лівій і правій частинах випливає рівність самих векторів.
2)
![]() ;
;
3)
![]() .
.
Виконаємо перестановку індексів і отримаємо:
![]() .
.
 .
.
Остаточно маємо, що
![]() .
.
Знайти: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 .
.
Розв’язання.
Як відомо
![]() ,
,
![]()
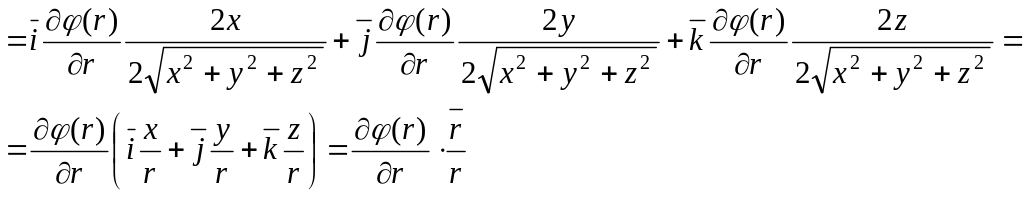
Використаємо наступну тотожність, доведену в попередній задачі:
![]() .
.
Тоді отримаємо:
![]() .
.
3)
Так як
![]()
Знайти дивергенцію та ротори таких векторів та
 ,
де
,
де
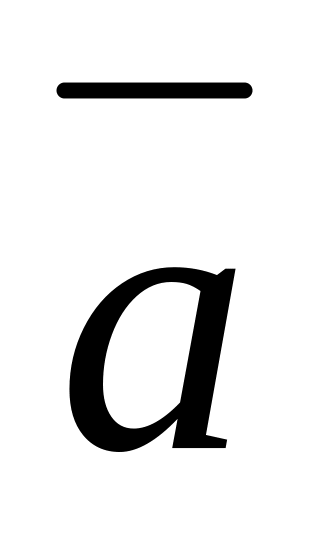 і
і
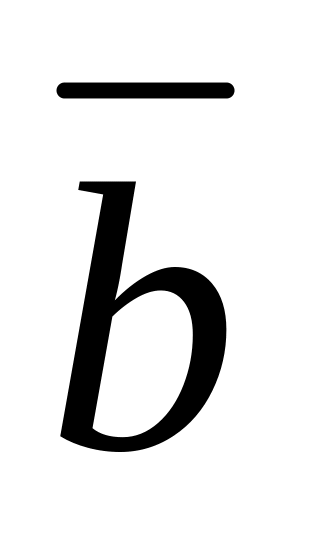 -
постійні вектори.
-
постійні вектори.
Розв’язання.
1)
![]() .
.
![]() .
.
Із рівності проекцій випливає і рівність самих векторів:
![]()
2).
![]() .
.
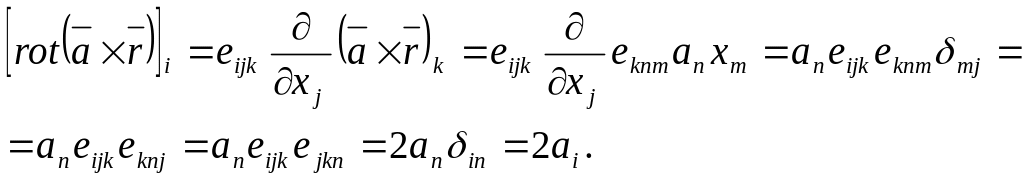
Звідси випливає, що
![]() .
.
Обчислити інтеграл
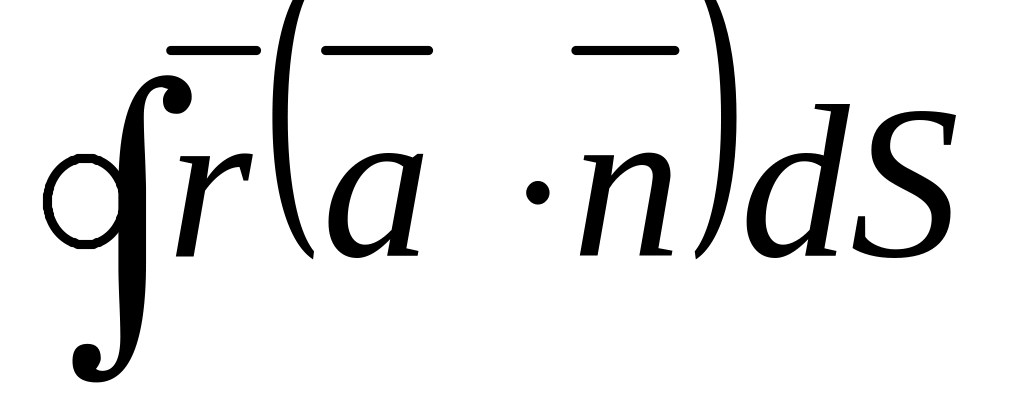 .
.
Розв’язання.
Помножимо скалярно інтеграл на постійний
вектор
![]() і використаємо теорему Гауса:
і використаємо теорему Гауса:
![]()
Так як вектор довільний, то
![]() .
.
Інтеграл по замкненому контуру
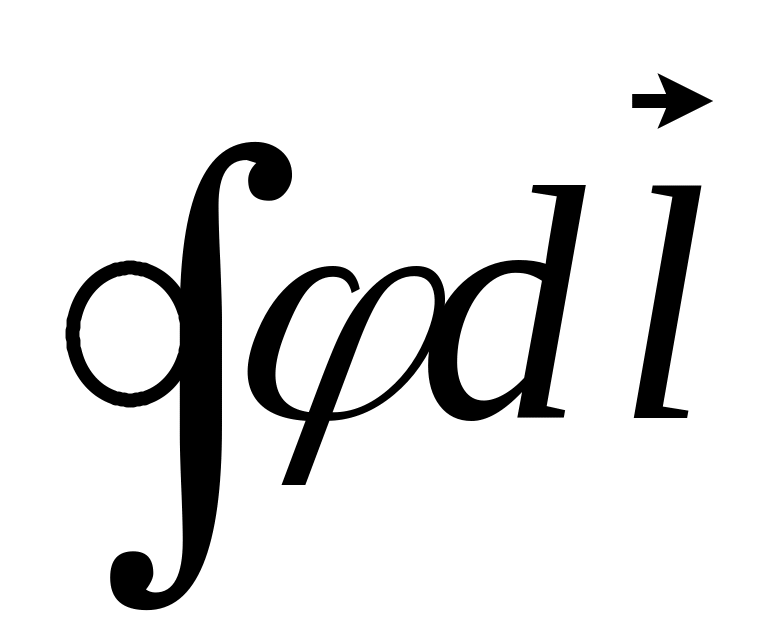 перетворити на інтеграл по поверхні,
яка опирається на цей контур.
перетворити на інтеграл по поверхні,
яка опирається на цей контур.
Розв’язання. Використаємо теорему .Стокса
![]() .
.
Помножимо наш інтеграл скалярно на постійний вектор .
![]() .
.
Виконаємо
циклічну перестановку векторів
,
![]() ,
,
![]() :
:
![]() .
.
Отже
![]() .
.
Довести, що компоненти антисиметричного тензора другого рангу при поворотах перетворюються як компоненти вектора.
Розв’язання.
Тензор
![]() має вигляд:
має вигляд:
 .
.
Звідси
видно, що
![]() ,
,
![]() .
.
Таким
чином у антисиметричного тензора
третього рангу всього три незалежних
компоненти:
![]() ,
,
![]() ,
,
![]() .
.
Позначимо
їх так:
![]() ,
,
![]() ,
,
![]() .
.
Ці
рівності можна записати в такому вигляді:
![]() ,
де
,
де
![]() -- повністю антисиметричний тензор
третього рангу.
-- повністю антисиметричний тензор
третього рангу.
Але,
так як
є тензор третього рангу, а
![]() - тензор другого рангу, то величини
- тензор другого рангу, то величини
![]() являються
компонентами тензора.
являються
компонентами тензора.
У всіх декартових системах координат задана сукупність величин , які мають такі властивості: при перестановці любих двох індексів змінює знак ,
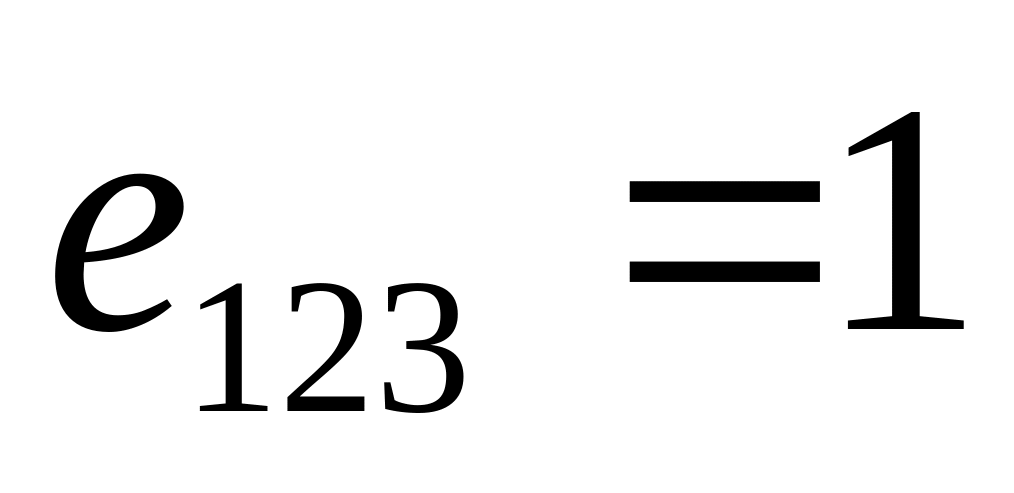 .
.
Довести, що є псевдотензором третього рангу (повністю антисиметричний одиничним псевдотензором третього рангу).
Розв’язання. Із 27 величин відмінні від нуля лише шість:
![]() .
.
Всі
інші мають мінімум по два однакових
індекси і тому в силу антисиметрії
перетворюються в нуль: (![]() ).
).
Запишемо зв’язок між компонентами тензора в двох ортонормованих базисах:

Якщо і=1, k=2, l=3, то визначник дорівнює 1.
Якщо і=2, k=1, l=3, то визначник дорівнює –1.
Тому:
 .
.
Компоненти
тензора
![]() однакові у всіх системах координат.
однакові у всіх системах координат.
При
допомозі тензора
можна записати вираз
![]() у формі
у формі
![]() ,
і
,
і
![]() вектори, а
псевдотензор, компоненти якого не
змінюють знак при інверсії. Так як
вектори, а
псевдотензор, компоненти якого не
змінюють знак при інверсії. Так як
![]() теж не змінює знак, то не змінює знак і
.
Отже
являється псевдотензором.
теж не змінює знак, то не змінює знак і
.
Отже
являється псевдотензором.
Довести, що
 ,
при
,
при
 .
.
Розв’язання.