Методика измерений

1. Ослабив винты 5, установите призмы 6 на заданное (преподавателем) расстояние. Закрепите винты.

2. Установите кронштейн 4 на одинаковом расстоянии от стоек. Закрепите винты.

3. Расположите образец на призмах так, чтобы гнездо индикатора находилось над средней частью по ширине образца.

4. Вставьте индикатор в гнездо, осторожно утопив его так, чтобы стрелка малой шкалы оказалась около метки 5 мм. Аккуратно зажмите индикатор винтом 9.

5. Измерьте штангенциркулем толщину b и ширину a образца. Измерьте линейкой расстояние между ребрами призм l. Установите поворотом кольца нуль на индикаторе.

6. Аккуратно поставьте на платформу гирю. Запишите (по красной шкале) показания индикатора.

7. Снимите с платформы гирю. Если стрелка сместилась с нулевой отметки, установить нуль. Повторите для контроля несколько раз измерения с тем же грузом.

8. Проведите аналогично п.7 измерение прогиба с гирями большей массы (массы брать около 1,2,3,4,5 кг).

9. Результаты занести в таблицу предложенной формы 16.1.

10. Рассчитайте модуль Юнга при каждом измерении и усредните результат.

11. Рассчитайте ошибку определения модуля Юнга E (достаточно рассчитать для одного опыта).

12. Значения модуля Юнга, совпадающие с учетом ошибки E друг с другом, т.е. не выходящие за границы значений (E_cp+ E) и (E_cp - E), позволяют определить истинное (среднее) значение модуля Юнга.

13. С учетом п.12 определить среднее значение модуля Юнга.

14. Ошибка модуля Юнга E определяется из рабочей формулы (16.9) как сумма частных ошибок всех величин, входящих в выражение :

, где

Контрольные вопросы.

1. Что такое модуль Юнга?

Модуль Юнга(модуль упругости)— коэффициент, характеризующий сопротивление материала к растяжению/сжатию при упругой деформации. Назван в честь английского физика XIX века Томаса Юнга.

2. Что такое абсолютное и относительное удлинение образца?

Линейная деформация (деформация растяжения) – деформация, при которой происходит изменение только одного линейного размера тела.

Количественно она характеризуется абсолютным Δl и относительным ε удлинением.

,

где Δl – абсолютное удлинение (м); l и l₀ – конечная и начальная длина тела (м).

• Если тело растягивают, то l > l₀ и Δl = l – l₀;

• если тело сжимают, то l < l₀ и Δl = –(l – l₀) = l₀ – l (рис. 9).

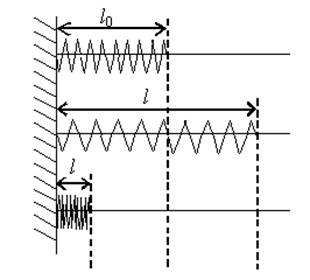
Рис. 9

или ,

где ε – относительное удлинение тела (%); Δl – абсолютное удлинение тела (м); l₀ –начальная длина тела (м).

3. Что такое механическое напряжение?

Состояние упруго деформированного тела характеризуют величиной σ, называемой механическим напряжением.

Механическое напряжение σ равно отношению модуля силы упругости F_упр к площади поперечного сечения тела S:

.

Измеряется механическое напряжение в Па: [σ] = Н/м² = Па.

Наблюдения показывают, что при небольших деформациях механическое напряжение σ пропорционально относительному удлинению ε:

. (2)

Эта формула является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным.

Коэффициент пропорциональности Е в законе Гука называется модулем упругости (модулем Юнга). Экспериментально установлено, что

модуль Юнга численно равен такому механическому напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза.

Докажем это: Из закона Гука получаем, что . Если модуль Юнга E численно равен механическому напряжению σ, то . Тогда .

Измеряется модуль Юнга в Па: [E] = Па/1 = Па.

Практически любое тело (кроме резины) при упругой деформации не может удвоить свою длину: значительно раньше оно разорвется. Чем больше модуль упругости Е, тем меньше деформируется стержень при прочих равных условиях (l₀, S, F). Таким образом, модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения или сжатия.

Закон Гука, записанный в форме (2), легко привести к виду (1). Действительно, подставив в (2) и , получим:

или ,

где .

4. Что такое коэффициент Пуассона?

Коэффициент Пуассона (обозначается как или ) характеризует упругие свойства материала. При приложении к телу растягивающего усилия оно начинает удлиняться (то есть продольная длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз изменяется поперечное сечение деформируемого тела при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно упругого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5. (Измеряется в относительных единицах: мм/мм, м/м).

5. Что такое абсолютное и относительное поперечное сжатие?

6. Какие из перечисленных характеристик относятся к материалу?

7. Какие из перечисленных характеристик относятся к образцу ?

8. Закон Гука и его физический смысл.

Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид

, (1)

где F_упр – модуль силы упругости, возникающей в теле при деформации (Н); Δl – абсолютное удлинение тела (м).

Коэффициент k называется жесткостью тела – коэффициент пропорциональности между деформирующей силой и деформацией в законе Гука.

Жесткость пружины численно равна силе, которую надо приложить к упруго деформируемому образцу, чтобы вызвать его единичную деформацию.

В системе СИ жесткость измеряется в ньютонах на метр (Н/м):

.

Коэффициент жесткости зависит от формы и размеров тела, а также от материала.

Закон Гука для одностороннего растяжения (сжатия) формулируют так:

сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.

9. Кривая зависимости  и ее характерные точки и участки.

10. Деформация сдвига, иллюстрация пластических деформаций.

Деформация сдвига. Деформацию сдвига можно наглядно продемонстрировать на модели твердого тела, представляющего собой ряд параллельных пластин, соединенных между собой пружинами (рис. 3). Горизонтальная сила F сдвигает пластины друг относительно друга без изменения объема тела. У реальных твердых тел при деформации сдвига объем также не изменяется. Деформации сдвига подвержены заклепки и болты, скрепляющие части мостовых ферм, балки в местах опор и др. Сдвиг на большие углы может привести к разрушению тела – срезу. Срез происходит при работе ножниц, долота, зубила, зубьев пилы и т.д.

11. В чем состоит суть данного метода измерения Е?

12. Зависит ли модуль Юнга от нагрузки и стрелы прогиба?

13. Чем отличается деформация прогиба от деформации растяжения?

14. Напишите формулу для модуля Юнга по прогибу.

Форма 16.1.

	a =0.05м	b =0.006м		l =0.52м
Масса гири m, кг		0,5кг	1,285кг		1,785кг	2,575кг
Показания индикатора n, дел		6	20		26	39,5
Сила F, Н		4,9Н	12,593Н		17,493Н	25,235Н
Стрела прогиба h, м		0,0006м	0,002м		0,0026м	0,00395м
Модуль Юнга E, Н/м2		2,66*1010 Н/м2	2,05*1010 Н/м2		2,19*1010 Н/м2	2,08*1010 Н/м2

Е_ср =2,245*10¹⁰ Н/м²

∆Е_m=0,027*10¹⁰ Н/м²

∆Е_l=0,015*10¹⁰ Н/м²

∆Е_h=0,022*10¹⁰ Н/м²

∆Е_a=0,003*10¹⁰ Н/м²

∆Е_b=0,066*10¹⁰ Н/м²

∆Е=0,077*10¹⁰ Н/м²

Е=2,245±0,077*10¹⁰ Н/м²

Вывод:

Модуль Юнга, с учётом погрешностей, равен Е=2,245±0,077*10¹⁰ Н/м².