
2 Способ решения задачи показан на рисунке 3.2.
Точки 12, 62, принадлежат контурным образующим конуса, и перенесем их по линиям связи на горизонтальную проекцию конуса. Точки 11 , 61 находятся на оси. Для нахождения дополнительных точек введем дополнительные секущие горизонтальные плоскости уровня (H, T, R, Q).

Рисунок 3.1. Построение линии пересечения конуса проецирующей плоскостью.
Фронтальные проекции точек 22, 102 находятся на пересечении следа данной плоскости Р2 и следа введенной плоскости Q2. Для построения горизонтальных проекций 21, 101 , построим в плоскости П1 фигуру сечения конуса плоскостью Q. Искомая фигура будет окружностью, радиус которой равен расстоянию от оси конуса до его контурной образующей, измеренный по следу плоскости Q2. Построив окружность, находим на ней с помощью линии связи проекции точек 21 , 101. Точки 23, 103 находятся по двум уже построенным проекциям. Остальные точки 3, 4, 5, 7, 8, 9 строятся аналогично. Видимость линии пересечения определяется точно так же как в первом способе решения задачи.
2. Для определения натуральной величины (н.в.) сечения применен метод замены плоскостей проекций. Дополнительная плоскость мысленно проводится перпендикулярно плоскости проекций П2 и параллельно следу Р2. Из каждой точки фронтальной проекции фигуры сечения проводим перпендикуляры к полученной оси сечения (рисунок 3.2). Точки 1 и 6 будут находиться на оси, положение остальных точек определяем, используя заменяемую плоскость П1. Например, на перпендикуляре, проходящем через точки 2 и 10, отложим расстояние [21101], измеренное на горизонтальной проекции фигуры сечения. Таким же образом определяется положение остальных точек. Соединив их между собой, получим натуральную величину сечения.
Задача 2. Построить линию пересечения многогранной поверхности и поверхности вращения.
Линия пересечения двух поверхностей строится способом вспомогательных секущих плоскостей (уровня или проецирующих). С их помощью определяют характерные точки и промежуточные точки линии пересечения. Плоскость следует выбирать так, чтобы линии ее пересечения с поверхностями проецировались в простейшие фигуры (окружности или прямые). Когда боковая поверхность цилиндра или призмы занимает относительно плоскости проекций проецирующее положение (образующие поверхности перпендикулярны этой плоскости проекций), то одна проекция линии пересечения становится известной без дополнительных построений, она совпадает с проекцией поверхности.
Порядок построения
В качестве примера рассмотрено пересечение конуса и треугольной призмы (рисунок 3.3).
Для построения линии пересечения вводим вспомогательные секущие фронтально-проецирующие плоскости, совпадающие с плоскостями граней призмы. В сечении конуса плоскостью Е получаем часть эллипса, плоскостью F – часть эллипса. Фронтальные проекции фигур сечения совпадают с проекциями граней призмы, поэтому необходимо построить только горизонтальные проекции. Для этого введем вспомогательные горизонтальные плоскости уровня R, T, Q, Y, V, H. Пересечение следов введенных плоскостей с фронтальной проекцией призмы дадут точки, принадлежащие искомой линии пересечения. Точки 3, 3', 8, 8' принадлежат ребрам призмы, точка 1 – контурной образующей конуса, эти точки являются характерными, остальные точки – дополнительными. Построение горизонтальных проекций найденных точек описано в задаче 1.
Определить видимость проекций линии пересечения и контуров заданных поверхностей (рисунок 3.3).
Задачи 3, 4. Пересечение тел вращения.
Для определения линии пересечения необходимо выбрать наиболее рациональный способ решения. При построении линии пересечения двух поверхностей нужно сначала найти характерные точки искомой кривой:
Точки, проекции которых лежат на проекциях контурных линий одной из поверхностей, а также точки, отделяющие видимую часть линии от невидимой;
«Крайние точки»: правые и левые, наивысшие и наинизшие, ближайшие и наиболее удаленные от плоскостей проекций.
На чертеже обязательно нужно показать построение опорных точек кривой, а также двух-трех промежуточных.
Задача 3. Построить линию пересечения двух поверхностей способом вспомогательных секущих плоскостей.
Вспомогательные секущие плоскости выбирают таким образом, чтобы в пересечении с данными поверхностями они давали наиболее простые линии (окружности, прямые линии). Для всех вариантов заданий в качестве вспомогательных секущих плоскостей могут быть выбраны плоскости уровня: горизонтальные и фронтальные.
Порядок построения:
Проводим вспомогательные секущие плоскости H, V, Y, Q, T, R (H2, V2, Y2, Q2, T2, R2) (рисунок 3.4).
Находим горизонтальные проекции линий пересечения секущих плоскостей с обеими пересекающимися поверхностями (сечения конуса – окружность, цилиндра – прямоугольник).
Находим общие точки пересечения построенных линий.
Соединяем последовательно построенные точки и получаем горизонтальную проекцию линию пересечения двух поверхностей.
Фронтальная проекция искомой линии будет совпадать с проекцией цилиндра.
Определим видимость проекций линии пересечения и контурных образующих заданных поверхностей.
Задача 4. Построить линию пересечения двух поверхностей способом вспомогательных секущих сфер.
Для построения линии пересечения поверхностей вращения с пересекающимися осями и общей плоскостью симметрии применяется способ вспомогательных секущих сфер. В основу этого способа положено свойство сферы пересекать соосную с ней поверхность вращения по окружности. Для того чтобы вспомогательная секущая сфера пересекала обе поверхности вращения по окружностям, центр сферы должен лежать в точке пересечения осей этих поверхностей.
Порядок построения:
Определяем радиус наименьшей сферы – эта сфера должна быть касательной к большей поверхности (рисунок 3.5).
Проводим секущую сферу СФ 1.
Определяем радиус наибольшей сферы – эта сфера должна проходить через точку пересечения контуров пересекающихся поверхностей,
наиболее удаленную от центра вспомогательных секущих сфер.
Проводим секущую сферу СФ 2.
Строим линии пересечения данной сферы с поверхностями вращения (конуса – А2 В2; цилиндра – С2 D2 и К2 L2).
Определяем общие точки при пересечении этих линий 12 и 22.
Построив нужное количество сфер, соединим последовательно общие точки и получим линию пересечения двух поверхностей.
Строим горизонтальную проекцию линии пересечения, используя линии связи и проекции линий пересечения соответствующей поверхности со сферами. Например, для построения точек 21, 21', 11, 11', необходимо на фронтальной проекции измерить расстояние от оси конуса до точки А2 (она принадлежит контурной образующей) и в горизонтальной проекции из центра окружности – проекции основания конуса, провести дугу окружности радиусом R, на которую затем спроецировать точки 12, 22.
Определим видимость проекций линии пересечения и контурных образующих данных поверхностей.
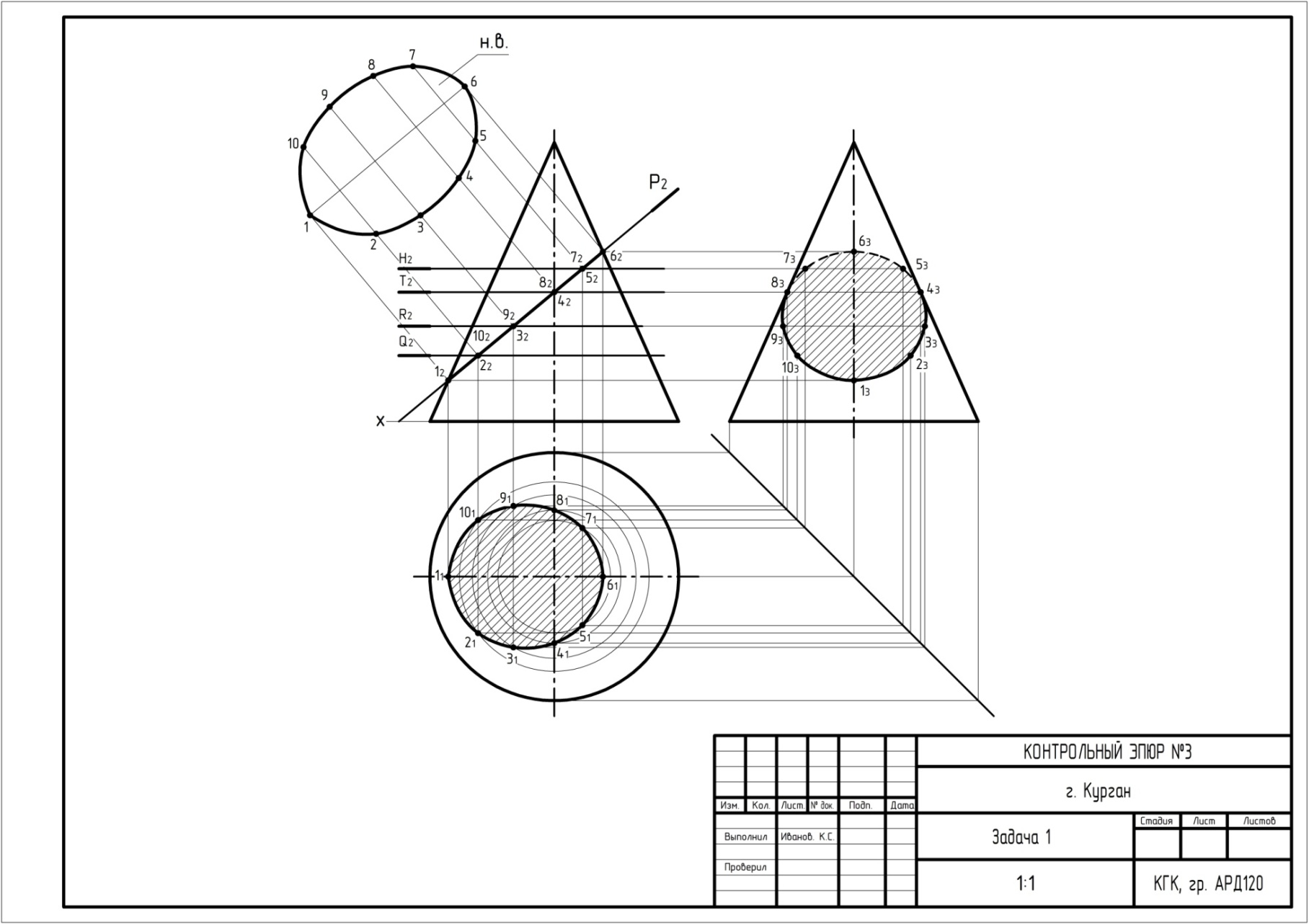
Рисунок 3.2. Пример выполнения задачи 1 эпюра № 3.

Рисунок 3.3. Пример выполнения задачи 2 эпюра № 3.

Рисунок 3.4. Пример выполнения задачи 3 эпюра № 3.

Рисунок 3.5. Пример выполнения задачи 4 эпюра № 3.
ПРИЛОЖЕНИЕ 1
