3.2. Определение размеров зубчатых колес

3.2.1. Вычислить размеры шестерни быстроходной ступени и тихоходной ступени по формулам (НВ < 350):

– цилиндрическая прямозубая передача

мм; (10)

– цилиндрическая косозубая передача

мм; (11)

– коническая передача

мм. (12)

В формулах (10), (11), (12) обозначено: – крутящий момент силы, передаваемый шестерней, Нм; – передаточное число быстроходной или тихоходной ступени; [ ] – допускаемое контактное напряжение, МПа; – отношение ширины венца зубчатого колеса к диаметру шестерни; – коэффициент нагрузки (K_НВ– коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца; – коэффициент, учитывающий динамическую нагрузку; – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями); – коэффициент ширины зубчатого венца конической передачи; коэффициент – прямозубая коническая передача; – косозубая коническая передача; – коническая передача с круговыми зубьями.

Штрихом отмечены величины, которые подлежат уточнению в процессе расчетов. На первом этапе ими задаются или рассчитывают их ориентировочные значения.

Ориентировочные значения коэффициентов на первом этапе можно принимать следующими:

 = 1,3 – косозубая цилиндрическая, прямозубая двух-поточная;

 = 1,4 – прямозубая, шевронная цилиндрическая, коническая косозубая и с круговым зубом;

 = 1,5 – коническая прямозубая;

 = 0,7...0,8 – косозубая цилиндрическая;

 = 0,8...0,9 – прямозубая;

 = 0,9...1,0 – шевронная;

 = 1,1...1,2 – косозубая двухпоточная;

 = 1,3...1,4 – прямозубая двухпоточная;

 = 0,285...0,30 – конические передачи.

Определить диаметры колес по формуле

,

где – передаточное число быстроходной (тихоходной) ступени.

3.2.2. Ориентировочно определить размеры редуктора

Рассчитать ширину колес по формулам:

– ширина венца зубчатого колеса ;

– ширина шестерни ;

– ширина венца конического колеса ;

– внешнее конусное расстояние конических передач

.

Вычислить углы делительных конусов ,

.

Определить диаметры валов редуктора по формуле

,

где – наибольшее значение крутящего момента сил на соответствующем валу; = (20...30) МПа – пониженное допускаемое касательное напряжение для материала вала.

Вычертить в масштабе 1:2 зубчатые колеса и валы согласно заданной кинематической схеме и показать руководителю проекта.

3.2.3. Уточнить параметры цилиндрической зубчатой передачи

 Определить межцентровое расстояние , мм.

 Определить модуль зацепления , мм

и согласовать с ГОСТом m = 1,0; 1,25; 1,5; 1,75; 2,0; 2,25; 2,5; (2,75); 3,0; (3,25); 3,5; (3,75); 4,0; (4,25); 4,5; 5,0; 5,5; 6,0; 6,5; 7,0; 8,0; 9,0... (значения модулей, указанные в скобках, желательно не применять).

 Определить суммарное число зубьев шестерни и колеса

(округлить до целого числа; = 0 – прямозубые, – косозубые, – шевронные).

 Определить число зубьев шестерни, , (округлить до целого числа ).

 Определить число зубьев колеса .

 Уточнить передаточное число (отклонение допустимо до 5 %).

 Уточнить угол наклона зуба ( определяется с точностью до секунды).

 Определить основные размеры зубчатой пары и разработать конструкцию колеса [4, с.140, 167; 3, с.15; 5, c.27, 33].

 Назначить степень точности изготовления зубчатых колес по окружной скорости [ 4, с.153 и др.].

, мс^–1.

После выбора значения модуля, зная число зубьев, можно уточнить диаметры зубчатых колес по формуле: d_i = m z_i.

3.2.4. Уточнить параметры конической зубчатой передачи

Принять число зубьев шестерни Z₁ (17...25). Определить число зубьев колеса Z₂ по формуле (округлить число зубьев Z₂ до целого числа).

Вычислить модуль зацепления или :

– прямозубые конические ;

– косозубые или с круговым зубом ,

(согласовать с ГОСТом (см. п.3.2.3.)).

Уточнить размеры зубчатых колес , .

Вычислить внешнее конусное расстояние :

– прямозубая коническая ;

– косозубая или с круговым зубом .

Вычислить среднее конусное расстояние :

– прямозубая коническая R_m = R_e – 0,5b;

– косозубая ( ) или с круговым зубом ( )

.

Вычислить нормальный модуль зацепления m = m_eR_m/R_e

.

(Нормальный модуль зацепления по ГОСТу не выбирается.)

Назначить степень точности по окружной скорости V = 4,310^–4 d₁, мс^–1, где d_i – диаметр шестерни в мм (см. табл. П4).

3.3. Проверка напряжений в зубьях зубчатых передач

3.3.1. Определить рабочие контактные напряжения и сравнить их с допускаемыми:

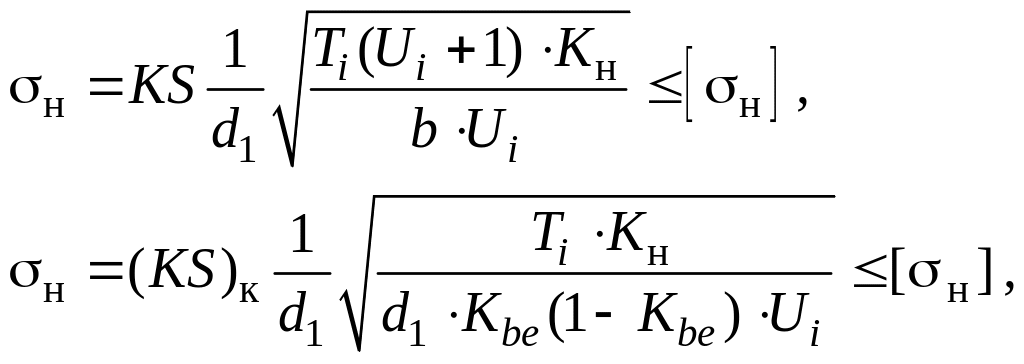(13)

где KS = 19200 – прямозубая цилиндрическая передача; KS = 16300 – косозубая, шевронная цилиндрическая; (KS)_к = 32240 – прямозубая коническая; (KS)_к = 24200 – коническая с круговым зубом; (KS)_к = 25400 – косозубая коническая; d₁ –диаметр делительной окружности шестерни, мм; b – ширина венца зубчатого колеса, мм; U_i – уточненное значение передаточного числа; – крутящий момент силы на том валу, где шестерня, Нм; – уточненное значение коэффициента нагрузки; – прямозубые передачи; + – косозубые передачи; – степень точности (целое число) ; – прямозубая цилиндрическая; – косозубая цилиндрическая; – прямозубая коническая; = 1 – косозубые цилиндрические передачи.

Прямозубые цилиндрические передачи:

– симметричная относительно опор;

– несимметричная относительно опор;

– двухпоточная.

Конические передачи:

;

– прямозубые цилиндрические и конические;

– косозубые цилиндрические и конические.

3.3.2. Определить рабочие напряжения изгиба и сравнить их с допускаемыми

 Цилиндрические прямозубые, косозубые, шевронные:

,

где – крутящий момент силы на том валу, где установлена шестерня, Нм; b – ширина венца колеса, мм; – модуль нормальный, мм; – делительный диаметр шестерни, мм; – коэффициент формы зуба; – приведенное число зубьев ( для прямозубых передач); – число зубьев шестерни, – число зубьев колеса; ; – коэффициент нагрузки; ; – шестая степень точности; – седьмая степень точности; – восьмая степень точности;

– цилиндрические прямозубые;

– цилиндрические косозубые.

Рабочие напряжения изгиба колеса определяются соотношением

.

 Конические прямозубые и косозубые:

,

где K_F = 2280 – прямозубые; K_F = 1500 – косозубые; – имеют тот же физический смысл, что и в формуле (13); – прямозубые, – косозубые, – подставляется уточненное значение; приведенное число зубьев , – косозубая коническая пе-редача; ;

– прямозубая коническая;

– косозубая и с круговым зубом конические передачи.

.

3.3.3. Проверка напряжений при перегрузках:

, (14)

где – контактное напряжение при перегрузках; – рабочее контактное напряжение, которое возникает при номинальном крутящем моменте; – допускаемое контактное напряжение при перегрузках; – максимальное значение момента сил сопротивления; – момент движущих сил (отношение / определяется из графика).

,

где , , , , – имеют тот же смысл, что и в формуле (14), но только для напряжений изгиба.

4. Эскизная компоновка редуктора

Этот вопрос необходимо решать, используя работы [9, с. 24-32; 10, с. 105].

5. Подбор подшипников

5.1. Расчет сил, действующих в зацеплении [11, с. 293; 3, с. 61, 83]

Определить окружную F_t, осевую F_a, радиальную F_r силы в зацеплении зубчатых передачах по формулам:

· цилиндрические передачи ,

,

,

где T_i – крутящий момент силы, передаваемый зубчатым колесом, диаметр делительной окружности которого равен d_i;  – угол наклона зуба (в прямозубых передачах  = 0);  – угол зацепления ( = 20);

 конические передачи прямозубые:

,

,

,

,

;

 конические передачи с круговыми зубьями для ведущего зубчатого колеса:

(15)

 для ведомого зубчатого колеса

(16)

В формулах (15), (16) надо брать верхний знак при совпадении винтовой линии зубьев и внешнего момента, нижний – в противном случае (F_t – направлена в противоположную сторону внешнего момента). Выбор направления действия сил в зацеплении см. рис. 4.

Рис. 4. Схема сил, действующих в зацеплении

5.2. Построение расчетных схем валов [12, с. 19; 3, с. 169]

5.3. Подбор подшипников

Подобрать подшипники по динамической грузоподъемности [9, с. 79...88], разработать конструкцию подшипникового узла, предусмотрев его фиксацию на валу и в корпусе, а также условия смазки и предохранения от пыли, грязи и абразивных частиц [11, с. 316; 9, с. 92, 149].

6. Подбор муфт [11, с. 456].

7. Расчет валов на статическую прочность,

выносливость и жесткость [12, с.20; 2, с.262, 263, 267]

8. Выбор посадок, расчет одной посадки

Составить расчетную схему и выписать исходные величины: d – диаметр вала, D – диаметр ступицы или диаметр впадин зубчатого колеса, – длина посадочного места, T – крутящий момент сил, передаваемых данным зубчатым колесом, f – коэффициент трения,  – коэффициент Пуассона, Е – модуль продольной упругости, и – высота микронеровностей вала и отверстия.

Рассчитать величину наибольшего натяга по формуле

,

где – величина необходимого удельного давления для передачи крутящего момента сил с вала на зубчатое колесо;

; ,

где – внутренний диаметр вала.

Вычислить расчетный натяг по зависимости

.

По величине выбрать посадку [9].

Проверить прочность соединяемых деталей.

Определить наибольшее удельное давление по наибольшему натягу выбранной посадки

.

Рассчитать эквивалентные напряжения по третьей теории прочности

,

где – главные напряжения.

Эквивалентные напряжение на внутреннем контуре колеса

,

где ; – сжимающее напряжение; – растягивающее напряжение.

Наибольшее эквивалентное напряжение сравнивается с пределом текучести.

Показать поле допуска для выбранной посадки.

9. Выбор смазки [9, с. 147; 3, с. 144]

10. Оценка неравномерности движения машины

Определить неравномерность движения машины по формуле

,

где – определяется из рис. 3,е;  – частота вращения тихоходного вала редуктора; I_п – приведенный момент инерции масс, определяемый по формуле

I_п = (I_р + I₁)(U_б U_т)² + I₂U²_т + I₃ ,

где I_р – момент инерции массы ротора двигателя; I₁, I₂, I₃ – моменты инерции вращающихся масс на быстроходном, промежуточном и тихоходном валах редуктора соответственно; U_б , U_т – передаточные числа быстроходной и тихоходной ступеней редуктора.

Момент инерции массы диска в общем случае определяется по зависимости

,

где b – ширина диска, м; D – диаметр диска, м;  – удельный вес материала диска, Н/м³ ; g – ускорение силы тяжести, м/с².