§ 5. Матрицы.

5.1. Найти обратную матрицу.

Общие сведения и расчётные формулы: по представленному заданию.

Пусть задана невырожденная квадратная матрица , и необходимо найти обратную ей матрицу . Общий алгоритм вычислений обратной матрицы определяется соответствием:

→ = = · ,

где – алгебраическое дополнение к элементу матрицы .

Вычисление обратной матрицы может проводиться двумя способами, каждый из которых по-разному проявляется в применении к конкретной матрице .

Способ-1. Используя выражение (4), выполняют действия:

1) Вычисляем определитель заданной матрицы: d = | |.

2) Если d =0, то поиск матрицы прекращается.

3) Если d ≠0, то матрица для заданной матрицы существует. Поиск матрицы продолжается.

4) Вычисляем матрицу , затем обратную матрицу = .

Способ-2. Используется связка двух матриц . К этой связке применяют элементарные преобразования с целью получить запись этой связки в виде: .

В качестве элементарных преобразований в этом случае принимаем такие преобразования:

▫ умножение строки связки матриц на число;

▫ прибавление к некоторой строке связки матриц другой строки, умноженной на число.

Примеры (и образец оформления):

Пример–1: Найти обратную матрицу для матрицы: .

Решение:

Способ-1. Используя выражение = , выполним действия:

1) Вычисляем определитель заданной матрицы: d =(1)= =(2)=1· –1.

Выполнены операции: (1): [R2]–[R3]; [R1]–[R2]. (2): применяем разложение по столбцу-1 и завершаем вычисление.

2) Так как d ≠0, то матрица для заданной матрицы существует. Поиск матрицы продолжается.

3) Вычисляем матрицу = , где = – алгебраическое дополнение к элементу матрицы .

При построении матрицы для вычисления алгебраического дополнения , соответствующего элементу , будем выделять соответствующий минор при помощи полосок картона, закрывая элемент горизонтальной и вертикальной полосками. Это позволит видеть любой выделяемый минор и легко записывать для дальнейшего использования! Указанные действия рекомендуется выполнять на черновике!

* Выделим миноры: к элементу ; к элементу ; к элементу :

	1											2											3
1					= –1;					1					= 38;					1					=–27,
		3	4							2	6		4							2	6	3
		-2	-3								5		-3								5	-2

и вычислим алгебраические дополнения , , выделенных миноров:

= = –1; = = 38; = = –27;

* Выделим миноры: к элементу ; к элементу ; к элементу :

	1											2											3
		5	7		= 1;						2		7		= –41;						2	5			= 29,
2										2										2
		-2	-3								5		-3								5	-2

и вычислим алгебраические дополнения , , выделенных миноров:

= = 1; = = –41; = = 29;

* Выделим миноры: к элементу ; к элементу ; к элементу :

	1											2											3
		5	7		= –1;						2		7		= 34;						2	5			= –24;
		3	4								6		4								6	3
3										3										3

и вычислим алгебраические дополнения , , выделенных миноров:

= = –1; = = 34; = = –24;

4). Учитывая результаты вычислений, можем записать: = · .

Способ-2. Записываем связку двух матриц : = . Далее одновременным преобразованием строк этой матрицы, добиваемся преобразования ее левой половины в единичную матрицу . Правая половина матрицы будет иметь вид .

1). Выполним операции: (1): [R2] –[R3]; [R1] –[R2]: имеем = .

2). Выполним операции: (2): [R2] –[R1]; [R3] –[R1] ·5. (3): [R2]+[R3]·2. Имеем:

=(2)→ =(3) → = .

3). Выполним операции: (4): [R2]+[R3]. (5): [R3]·( –1), где R – строка. Имеем:

=(4) → =(5) → .

4). Получена обратная матрица: в правой половине связки матриц.

Замечание: часто сравнивают применение Способа-1 и Способа-2 по трудоёмкости вычисления матрицы , после чего отдают предпочтение одному из них; сравнивают также по степени защищённости указанных способов от вычислительных ошибок; на самом деле оба способа играют важную роль в обучении предмету!

Ответ: = .

Варианты индивидуальных заданий:

Вар.	Задание:	Вар.	Задание:	Вар.	Задание:
1.		2.		3.
4.		5.		6.
7.		8.		9.
10.		11.		12.
13.		14.		15.
16.		17.		18.
19.		20.		21.
22.		23.		24.
25.		26.		27.
28.		29.		30.

5.2. Найти ранг матрицы: а) методом окаймляющих миноров; б) приведением к ступенчатому виду.

Общие сведения и расчётные формулы: по представленному заданию.

Максимальное число линейно независимых столбцов (строк) матрицы (то есть число столбцов (строк), входящих в любую подсистему линейно независимых столбцов (строк)), называется рангом этой матрицы; обозначение – . Мы применяем два способа вычисления ранга матрицы.

Способ-1. Метод окаймляющих миноров.

Получено правило вычисления ранга матрицы:

– при вычислении ранга матрицы переходят от миноров меньших порядков, к минорам больших порядков;

– если уже найден минор -го порядка не равный нулю, то следует переходить к окаймлению его минором ( +1)-го порядка;

– если все окаймляющие миноры ( +1)-го порядка равны нулю, то ранг матрицы равен числу .

Способ-2. Приведение к ступенчатому (диагональному) виду применением элементарных преобразований (не меняют ранга!):

– транспозиция двух строк или столбцов;

– умножение строки (столбца) на число, не равное нулю;

– прибавление к строке (столбцу) другой строки (столбца), умноженной на некоторое число;

– после получения диагональной формы матрицы число единиц на главной диагонали определяет ранг матрицы.

Замечания: 1) правило приведения матрицы к диагональному виду применяют обычно в тех случаях, когда требуется только определить ранг матрицы: следить за всеми перестановками строк и столбцов неудобно;

2) если столбцы не переставлять (за одними строками следить не так сложно!), а единицы на главной диагонали получать способом уравнивания коэффициентов, то метод вполне удобен для выделения в системе векторов-строк максимальной линейно независимой подсистемы векторов.

Замечание: при выполнении задания каждый применяет оба из указанных способов.

Примеры (и образец оформления):

Пример–1: Найти ранг матрицы: методом окаймляющих миноров.

Решение:

1). Так как в матрице есть элементы не равные нулю, то ранг матрицы . Окаймление любого из них приводит к минору 2-го порядка.

2). Не равных нулю миноров 2-го порядка несколько. Это значит, что . Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу:

	4	3	-5	2	3
	8	6	-7	4	2
1	4	3	-8	2	7
2	4	3	1	2	-5
3	8	6	-1	4	-6
	3	2	1

3). Окаймляющие миноры будем обозначать: , где – указывает номер отмеченной для окаймления строки, – указывает номер отмеченного для окаймления столбца. Тогда можем записать:

= =(–5) –(–7) +(–8) =m₁·(24)–h₁·(8)+g₁·(–8)= (–5)·(24)–(–7)·(8)+(–8)·(–8)=0;

Замечание: параметры: m₁, h₁, g₁ изменяются при переходе к минорам , числа: (7), (–14), (–7) не изменяются. Это позволяет применить единый шаблон вычислений!

= = m₂·(24)–h₂·(8)+g₂·(–8)= 3·(24)–6·(8)+3·(–8)=0;

= = m₃·(24)–h₃·(8)+g₃·(–8)= 4·(24)–8·(8)+4·(–8)=0;

= =(–5) –(–7) + =m₁·(–24)–h₁·(–16)+g₁·(–8)=(–5)·(–24)–(–7)·(–16)+1·(–8)=0;

Замечание: параметры: m₁, h₁, g₁ изменяются при переходе к минорам , числа: (–24), (–16), (–8) не изменяются. Это позволяет применить единый шаблон вычислений!

= = m₂·(–24)–h₂·(–16)+g₂·(–8)=3·(–24)–6·(–16)+3·(–8)=0.

= = m₃·(–24)–h₃·(–16)+g₃·(–8)=4·(–24)–8·(–16)+4·(–8)=0.

= =(–5) –(–7) +(–1) =m₁·(–32)–h₁·(–24)+g₁·(–8)=

=(–5)·(–32)–(–7)·(–24)+(–1)·(–8)=0;

Замечание: параметры: m₁, h₁, g₁ изменяются при переходе к минорам , числа: (–28), (–24), (–8) не изменяются. Это позволяет применить единый шаблон вычислений!

= = m₂·(–32)–h₂·(–24)+g₂·(–8)= 3·(–32)–6·(–24)+6·(–8)=0.

= = m₃·(–32)–h₃·(–24)+g₃·(–8)= 4·(–32)–8·(–24)+8·(–8)=0.

4). Так как все окаймляющие миноры 3-го порядка равны нулю, то .

Ответ: = 2.

Пример–2: Найти ранг матрицы: = элементарными преобразованиями.

Решение:

1). Применим элементарные преобразования к заданной матрице:

=(1)→ =(2)→ =(3) → .

Операции: (1): [C5]+[C2]–[C4]; [C4]+[C1]+[C2]; [C3]–[C1]+[C2] . (2): [C1]–[C2]·3. 3): делим [R5] на 13 и при помощи числа 1 обнуляем элементы [C2]; делим [R4] на 67 и при помощи числа 1 обнуляем элементы [C1].

2). Видим (!): ранг матрицы равен 2.

Ответ: = 2.

Пример–3: Найти ранг матрицы: двумя способами: методом окаймляющих миноров и применяя элементарные преобразования.

Решение:

Способ-1. Метод окаймляющих миноров.

1). Так как в матрице есть элементы не равные нулю, то ранг матрицы . Окаймление любого из них приводит к минору 2-го порядка.

2). Не равных нулю миноров 2-го порядка несколько. Это значит, что . Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу:

	2	-3	3	2	-2
	2	9	3	4	2
1	3	-3	-1	2	2
2	3	-3	3	-1	-5
	3	2	1

3). Окаймляющие миноры будем обозначать: , где – указывает номер отмеченной для окаймления строки, – указывает номер отмеченного для окаймления столбца. Тогда можем записать:

= =3· –3· +(–1)· =m₁·(4)–h₁·(8)+g₁·(12)=3·(4)–3·(8)+(–1)·(12) 0;

Это значит, что и необходимо вычислить окаймляющие миноры 4-го порядка:

	2	-3	3	2	-2
	2	9	3	4	2
	3	-3	-1	2	2
1	3	-3	3	-1	-5
	2	1

3). Окаймляющие миноры будем обозначать: , где – указывает номер отмеченной для окаймления строки, – указывает номер отмеченного для окаймления столбца. Тогда можем записать:

= =(–3)· –9· +(–3)· –(–3)· ,

или: = m₁·(12)–h₁·(32)+g₁·(6) –q₁·(–24)= (–3)·(12)–9·(32)+ (–3)·(6) –(–3)·(–24) 0.

4). Так как минор 4-го порядка не равен нулю, то .

Ответ: .

Способ-2. Приведение к ступенчатому (диагональному) виду применением элементарных преобразований (не меняют ранга!):

1). Применим элементарные преобразования к заданной матрице:

=(1)→ =(2)→ =(3)→ .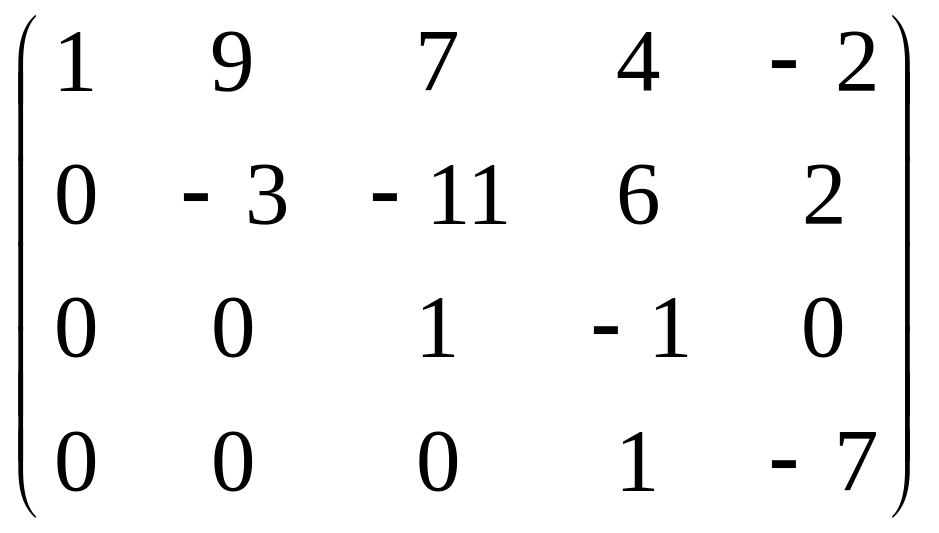

Операции: (1): [R1]+[R2]–[R3]; [R4] –[R3]; [R3]–[R2] –[R1] . (2): [R3]–[R2]·2; [R2]–[R3]·3; разделим [R2] на 22 и поменяем местами [R2] и [R3]. 3): [R4]–[R3]·4.

2). Видим (!): ранг матрицы равен 4.

Ответ: .

Варианты индивидуальных заданий:

Вар.	Задание:	Вар.	Задание:
1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.