- •Тема 3.2 Дифференциальное исчисление
- •1)Написание рефератов, докладов
- •2)Исследовательская работа. Решение задач
- •Тема 4.1. Неопределенный интеграл
- •1)Исследовательская работа, решение задач
- •Тема 4.2 Определенный интеграл
- •1)Написание рефератов, докладов.
- •2)Исследовательская работа, решение задач.
- •Контрольные задачи к разделу
- •Контрольные задачи к разделу «Дифференциальное исчисление функций нескольких переменных»
- •Раздел 6. Двойные интегралы
- •Тема 6.1. Двойные интегралы
- •Контрольные задачи к разделу
- •Тема 7.1. Числовые ряды
- •Тема 7.2. Степенные ряды
Тема 3.2 Дифференциальное исчисление
1)Написание рефератов, докладов
-Физический смысл второй производной
2)Исследовательская работа. Решение задач
Вычисление производных сложных функций
Найти производные следующих функций:
3.2.1.
⨍(x
)=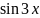 ;
3.2.2.
⨍(x
)=
;
3.2.2.
⨍(x
)=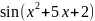 ;
3.2.3.
⨍(x
)=
;
3.2.3.
⨍(x
)=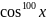 ;
;
3.2.4.
⨍(x
)=
tg(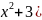 ;
3.2.5.
⨍(x
)=
;
3.2.5.
⨍(x
)=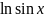 ;
3.2.6.
⨍(x
)=
;
3.2.6.
⨍(x
)= ;
;
3.2.7.
⨍(x
)=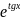 ;
3.2.8.
⨍(x
)=
;
3.2.8.
⨍(x
)=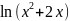 ;
3.2.9.
⨍(x
)=
;
3.2.9.
⨍(x
)=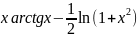 ;
;
3.2.10.
⨍(x
)=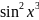 ;
3.2.11.
⨍(x
)=
;
3.2.11.
⨍(x
)=
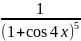 ;
3.2.12.
⨍(x
)=
;
3.2.12.
⨍(x
)=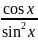 +
+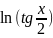 ;
;
3.2.13.
f(x)=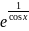 ;3.2.14.
f(x)=
;3.2.14.
f(x)=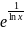 ;3.215.
f(x)=
;3.215.
f(x)=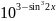 ;3.2.16.
f(x)=sin(
;3.2.16.
f(x)=sin(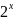 )
;
)
;
3.2.17.
f(x)=arccos(1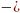 2x);
3.2.18.
f(x)=arcsin(
2x);
3.2.18.
f(x)=arcsin(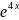 );
3.2.19.
f(x)=arctgln(5x+3);
);
3.2.19.
f(x)=arctgln(5x+3);
3.2.20.
f(x)=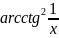 ;
3.2.21.f(x)=tgsincosx;
3.2.22.
f(x)=
;
3.2.21.f(x)=tgsincosx;
3.2.22.
f(x)=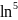 sinx;
3.2.23. f(x)=
sinx;
3.2.23. f(x)= ;
3.2.24.
f(x)=ln(x+1+
;
3.2.24.
f(x)=ln(x+1+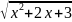 );
3.2.25.
f(x)=
+ln(tg
);
3.2.25.
f(x)=
+ln(tg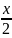 );
3.2.26.
f(x)=
);
3.2.26.
f(x)=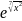 ;
3.2.27.
f(x)=ln(sin
x+
;
3.2.27.
f(x)=ln(sin
x+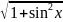 );
);
3.2.28.
f(x)=arcsin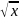 ;
3.2.29.
f(x)=
;
3.2.29.
f(x)=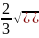 ;
3.2.30.
f(x)=
;
3.2.30.
f(x)=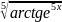 .
.
3.2.31.
y=tg(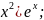 3.2.32.y=
3.2.32.y=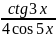 ;
3.2.33.
y=
;
3.2.33.
y=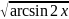 ; 3.2.34.
y=arcos(
; 3.2.34.
y=arcos(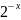 );
3.2.35.y=
);
3.2.35.y=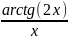 ;
3.2.36.y=
;
3.2.36.y=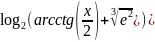 ;
3.2.37.y=(2/x+3)
;
3.2.37.y=(2/x+3)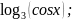 3.2.38.
y=
3.2.38.
y= ;
3.2.39.
y=
;
3.2.39.
y= arcctg(1+2
arcctg(1+2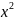 );
3.2.40.y=
);
3.2.40.y=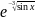 +
ln
+
ln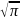 ;
3.2.41.
y=ln(ln
x); 3.2.42.
y=ctg
x
;
3.2.41.
y=ln(ln
x); 3.2.42.
y=ctg
x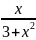 ;
3.2.43.y=
;
3.2.43.y=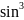 (3-x);
3.2.44.
y=arcsin(arcos
x); 3.2.45.
y=
(3-x);
3.2.44.
y=arcsin(arcos
x); 3.2.45.
y=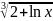 ;
;
3.2.46.
y=x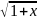 tg
x.
tg
x.
Найдем
отдельно случай, когда нужно найти
производную функции вида y=u(x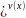 .
Воспользуемся логарифмическим тождеством
a=
.
Воспользуемся логарифмическим тождеством
a=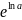 .
Так как ln(u(x
=v(x)
ln
(u(x)),
то y=u(x
=
.
Так как ln(u(x
=v(x)
ln
(u(x)),
то y=u(x
=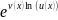 и
y′=(u(x
и
y′=(u(x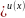 )′=(
)′=
)′=(
)′=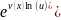 (u(x)ln(u(x))′=u(x
(v(x)ln(u(x)).
(u(x)ln(u(x))′=u(x
(v(x)ln(u(x)).
Таким образом,y′=(u(x ) ′=u(x (u(x)ln(u(x))′.
Пример
1. Найти
производную функции y=(sinx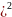 .
▲
y′=(sin
.
▲
y′=(sin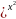 (
ln(sinx))′=(sin
x
(2x
ln sin x+
(
ln(sinx))′=(sin
x
(2x
ln sin x+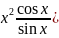 .
▲
.
▲
? Вопросы для самопроверки
1.
Дайте
определение производной функции y=f(x)
в точке
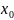 .
.
2. Каков геометрический смысл производной функции y=f(x) в точке ?
3.
Дайте определение касательной к графику
функции y=f(x)
в точке
 ;
f(y=f(
))
и напишите уравнение касательной.
;
f(y=f(
))
и напишите уравнение касательной.
4. Каков физический смысл производной функции y=f(x) в точке ?
5. Может ли функция, имеющая производную в точке, быть непрерывной в этой точке?
6. Дайте определение дифференциала функции в точке .
7. Каков геометрический смысл дифференциала?
8. Сформулируйте теорему о производной сложной функции
Проведите полное исследование следующих функций и постройте их графики:
3.3.1.
y= (x-10
;
3.3.
2.
(x-10
;
3.3.
2.
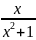 ;
3.3.3.
y=
;
3.3.3.
y=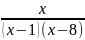 ;
3.3.4.
y=
;
3.3.4.
y=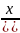 ;
;
3.3.5.
y=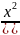 ;
3.3.6.
y=
;
3.3.6.
y=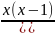 ;
3.3.7.
y=
;
3.3.7.
y=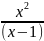 ;
3.3.8.
y=
;
3.3.8.
y=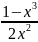 ;
;
3.3.9.
y=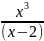 ;
3.3.10.
y=(x+1)
;
3.3.10.
y=(x+1) 3.3.11.
y=
3.3.11.
y=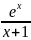 ;
3.3.12.
y=
;
3.3.12.
y=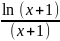 ;
;
3.3.13.
y=(x+1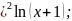
Тема 4.1. Неопределенный интеграл
1)Исследовательская работа, решение задач
Упражнения. Вычислить следующие интегралы:
1.
 10.
10.
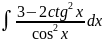
2.
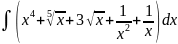 11.
11.
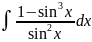
3.
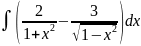 12.
12.
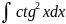
4.
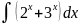 13.
13.
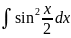
5.
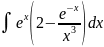 14.
14.
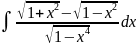
6.
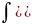 15.
15.
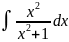
7.
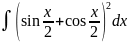 16.
16.
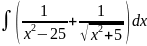
8.
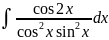 17.
17.
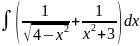
9.
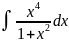 18.
18.
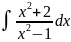
?Вопросы для самопроверки
1. В чем состоит метод непосредственного интегрирования?
2. Напишите формулу замены переменной в неопределенном интеграле. При каких условиях эта формула справедлива?
3. Напишите формулу интегрирования по частям. При каких условиях эта формула справедлива?
4. Какие интегралы наиболее удобно вычислять интегрированием по частям?
5. Каково назначение рекуррентных формул?
Контрольные задачи к разделу
Применяя метод замены переменной, вычислить следующие интегралы:
4.1.1.
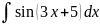
4.1.
2.
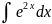
4.1.3.
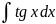
4.1.4.
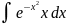
4.1.5.
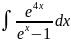
4.1.6.
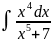
4.1.7.
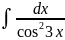
4.1.8.
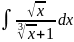
4.1.9.
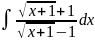
4.1.10.
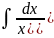
4.1.11.

4.1.12.
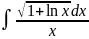
4.1.13.
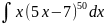
4.1.14.
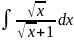
4.1.15.
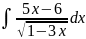
4.1.16.
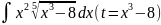
4.1.17.
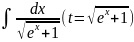
4.1.18.
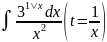
4.1.19.
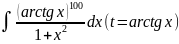
4.1.20.
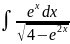
4.1.21.
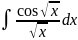
4.1.22.
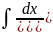
С помощью метода интегрирования по частям вычислить следующие интегралы:
4.1.23.
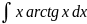
4.1.24.
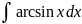
4.1.25.
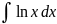
4.1.26.
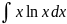
4.1.27.
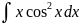
4.1.28.
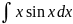
4.1.29.
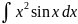
4.1.30.
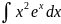
4.1.31.
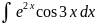
4.1.32.
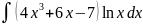
4.1.33.
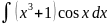
4.1.34.