
ЛАБОРАТОРНАЯ РАБОТА № 4
Тема: МОДЕЛИ ОПТИМИЗАЦИИ. ЛИНЕЙНЫЕ МОДЕЛИ
Цель работы: Научиться рассчитывать и анализировать линейные модели с помощью инструмента «Поиск решения» табличного процессора EXCEL 2007 и принимать решения на основе анализа.
Бюджет времени: 4 часа.
ЗАДАНИЯ:
Прочитайте лекцию и дополнительные теоретические сведения по теме.
Выучите определения.
Подготовьте отчет по лабораторной работе.
ОТЧЕТ ДОЛЖЕН СОДЕРЖАТЬ:
Результаты выполнения заданий.
Формулировку решений руководства на основании полученных результатов.
Ответы на контрольные вопросы.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
Назовите типовые задачи оптимизации.
Перечислите основные этапы решения задач оптимизации.
Как провести анализ решаемых задач?
Что такое оптимальный подбор исходных данных по заданному значению результата?
Запишите общий случай задач оптимизации.
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕМЕ:
При решении оптимизационных задач с помощью Поиск решений необходимо различать линейные и нелинейные модели. Под линейными понимаются модели, в которых связь между ограничениями на неизвестные и целевой ячейкой описывается линейными функциями. Общий вид линейной функции: Y=AX1+BX2+…+CXn, где A, B, C – константы, X1, X2, X3 – переменные, Y – результирующие значение.
Линейное программирование – наиболее развитый раздел математического программирования, вычислительные средства которого позволяют находить глобальный оптимум линейной задачи оптимизации.
Большинство экономических и управленческих задач возможно описать линейными моделями – именно этим обстоятельством объясняется успех практического использования линейных моделей и алгебраических методов для решения задач планирования и управления на уровне отдельных организаций, предприятий и даже отраслей производства.
Для решения линейных моделей целесообразно применять методы оптимизации линейных задач.
Именно этот математический результат лежит в основе симплекс-метода – для поиска оптимума нужно в определенном порядке пересмотреть некоторое количество вершин, используя несложный алгоритм последовательного улучшения значения целевой функции. Мощные и эффективные средства линейного программирования определенным образом используются и в целочисленном программировании для решения более сложных задач оптимизации.
Если выражение для целевой ячейки и выражения для ограничений являются линейными, то можно применять быстрые и надежные методы поиска решения. Для использования именно линейных методов следует установить параметр Линейная модель в окне Параметры поиска решений (Solver Options). Если этот параметр не установить, то даже для линейной задачи будут использоваться более общие методы.
Ниже рассмотрены некоторые практические примеры задач оптимизации, которые относятся к линейным моделям:
Задание 1: «ПЛАН ПРОИЗВОДСТВА»
Постановка задачи.
Предприятие имеет запасы 4-х видов ресурсов (мука, жиры, сахар, финансы), с которых производится 2 виды продуктов (хлеб и батон) (рис.59).
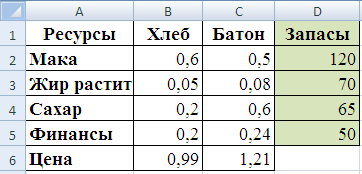
Рис.56. Запасы (ресурсы) предприятия
Известны:
нормы расходов ресурсов на производство единицы продукции;
запасы ресурсов;
цены продуктов;
спрос на хлеб.
Найти оптимальный план производства, при котором доход от реализации произведенной продукции должен быть максимальный.
Экономико-математическая модель.
Найдите план производства (количество хлеба и батонов) при котором:
Доход =0,99 * количество хлеба +1,21* количество батонов => мах.
При ограничениях:
0,6*количество хлеба +0,5* количество батонов <=120
0,05* количество хлеба +0,08* количество батонов <=70
0,2* количество хлеба +0,6* количество батонов <=65
0,2* количество хлеба +0,24* количество батонов <=50
(120<= количество хлеба, 150 <= количество батонов) =>0
Решение в Excel.
Создайте таблицу с формулами, которые связывают план, ограничения и целевую функцию (Доход) (рис.60):

Рис.56. Пример выполнения задания
В столбце «Затрачено» в каждую ячейку вводим формулу вычисления количества использованных ресурсов.
В ячейку Е7 вводим формулу расчета «Дохода».
Совет. Если таблицу разместить так, как показано, достаточно ввести формулу в первую ячейку, зафиксировать абсолютные координаты плана (нажать F4, чтобы появились символы $) и протянуть это формулу (маркером автозаполнения) к строке Цена.
Запустите команду Поиск решений командой Данные=>Поиск решения (в Excel 2007). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения введите соответствующие адреса ячеек.
Так как это линейная модель, то в окне Параметры поиска решений установите переключатель в положение Линейная модель и Неотрицательные значения. Нажмите кнопку Выполнить и в появившемся окне Результаты поиска решения выведите отчет.

Рис.57. Окно «Поиск решения»
Анализ результата выполнения.
Чтобы получить максимальный доход в размере 202,21 ден. ед. необходимо производить 151,92 ед. хлеба и 57,69 ед. батона. Из отчета видим, что ресурсы Мука и Сахар дефицитные, т.к. потрачены полностью.
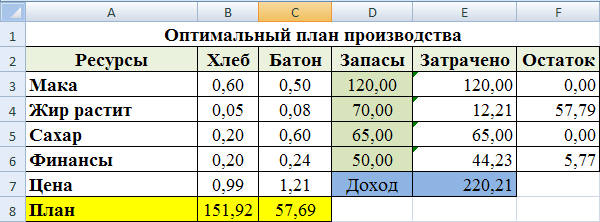
Рис.58. Результат расчетов инструмента «Поиск решения»
Очевидно, что хлеб и батоны должны быть целыми числами, после полученного отчета и анализа результата, мы можем, например, в нашей модели увеличить запас Сахара на 1 единицу, и снова выполнить процедуру Поиск решений, добавив ограничение относительно целочисленных значений плана. Результат расчета модели после редакции данных: чтобы получить максимальную прибыль в размере 221,1 д. ед. нужно производить 150 ед. хлеба и 60 ед. батонов.
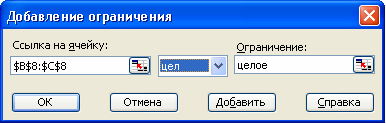
Рис.59. Редактирование условий для «Поиска решений»
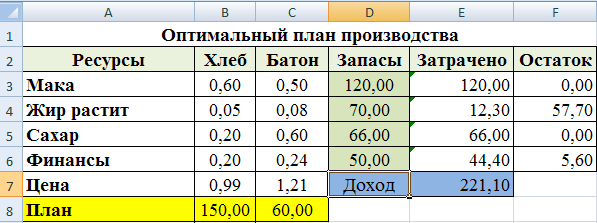
Рис.60. Построение модели по отредактированным условиям
Задание 2: «КУПИТЬ ИЛИ ПРОИЗВОДИТЬ?»
Постановка задачи.
Завод получил заказ на выпуск приборов 3 типов, для их производства приобретены материалы 2 типов. Если этих запасов окажется мало, завод обязуется докупить часть недостающих приборов на другом заводе. Нужно определить план исполнения заказа, при котором затраты будут минимальные. На рисунке 65 представлены данные относительно заказа, запасов, норм затрат материалов и затрат на производство, а так же покупку приборов.
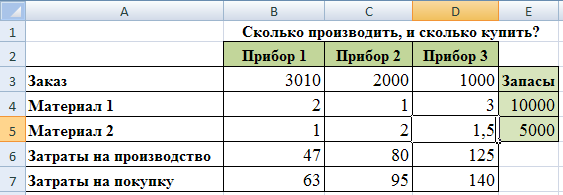
Рис.61. Исходные данные задания 2
