2.2 Дифференциальное уравнение равновесия Эйлера

В состоянии относительного покоя частицы жидкости не перемещаются относительно друг друга. При этом силы внутреннего трения отсутствуют, что позволяет считать жидкость идеальной.

В состояние относительного покоя форма объема жидкости не изменяется, и она, подобно твердому телу, перемещается как единое целое. Так, жидкость находится в относительном покое в перемещающемся сосуде (например, в цилиндре), внутри вращающегося с постоянной угловой скоростью барабана центрифуги и т.д. В подобных случаях покой рассматривают относительно стенок движущегося сосуда.

Жидкость в неподвижном сосуде находится в абсолютом покое (относительно поверхности земли), который в таком понимании является частным случаем относительного покоя.

Независимо от вида покоя на жидкость действуют силы тяжести и давления. В случае относительного покоя следует учитывать также силу инерции переносного (вместе с сосудом) движения жидкости.

Соотношение между силами, действующими на жидкость, которая находится в состоянии покоя, определяющие условия равновесия жидкости, выражается дифференциальными уравнениями равновесия Эйлера.

В объеме жидкости, находящейся в покое, выделим элементарный параллепипед объемом dV с ребрами dх, dy, dz, расположенными параллельно осям координат x,y,z. Сила тяжести, действующая на параллепипед будет равна .

Сила гидростатического давления на любую из граней параллепипеда равна произведению гидростатического давления на площадь этой грани.

Будем считать, что давление является функцией всех трех координат

Выясним вид этой функции, т.е. закон распределения гидростатического давления по объему жидкости.

Рис. 2.1.

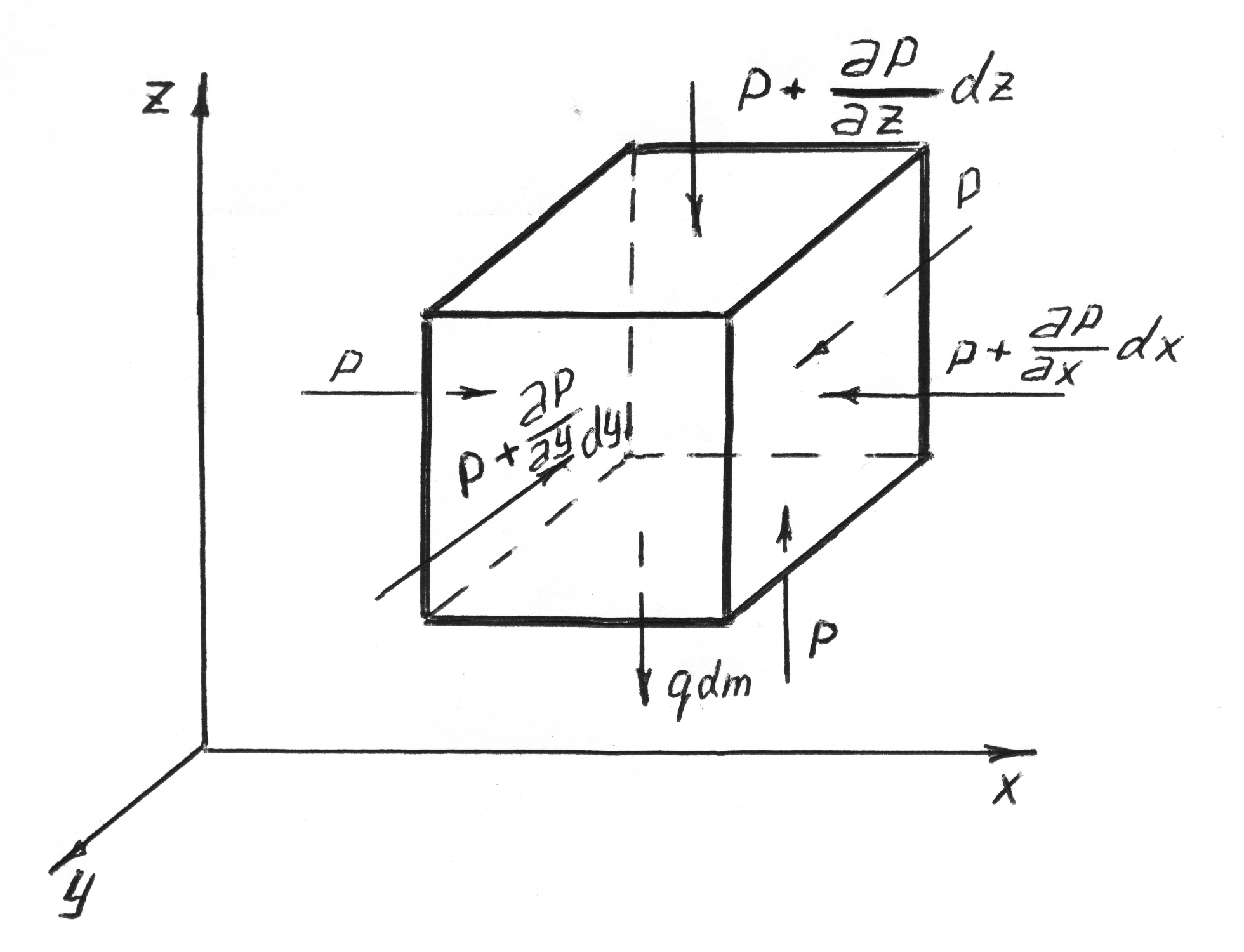
Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю.

В противном случае происходило бы перемещение жидкости.

Рассмотрим сумму проекций сил на ось z.

Сила гидростатического давления действует на нижнюю грань параллелепипеда по нормали к ней и ее проекции на ось z равна . Если изменение гидростатического давления в данной точке в направлении оси z равно , то по всей длине ребра dz оно составит . Тогда гидростатическое давление на противоположную (верхнюю) грань равно и проекция силы гидростатического давления на ось z

.

Проекция равнодействующей силы давления на ось z.

.

Сумма проекций сил на ось z равна нулю, то есть

(1)

или, учитывая, что объем параллелепипеда , получим

Проекции сил тяжести на ось х и у равны нулю. Поэтому сумма проекций сил на ость х

Откуда после раскрытия скобок и сокращения находим

, (2)

или

.

Соответственно для оси у

, (3)

или

.

Таким образом, условия равновесия элементарного параллелепипеда выражаются системой уравнений

(4)

Уравнения (4) представляют собой дифференциальные уравнения равновесия Эйлера.

Для получения закона распределения давления во всем объеме покоящейся жидкости следует проинтегрировать систему уравнений (4). Интегралом этих уравнений является основное уравнение гидростатики, широко используемое в инженерной практике.