4.2 Тепловые балансы

Согласно уравнению теплового баланса тепло, отдаваемое более нагретым теплоносителем, затрачивается на нагрев более холодного теплоносителя, и некоторая относительно небольшая часть тепла расходуется на компенсацию потерь тепла аппаратом в окружающую среду. Величина тепловых потерь в теплообменных аппаратах, покрытых тепловой изоляцией, не превышает 3 5 % полезно используемого тепла. Поэтому в расчетах потерями можно пренебречь. Тогда тепловой баланс выразится равенством

где Q – тепловая нагрузка аппарата;

Q₁ – количество тепла отданного более нагретым теплоносителем;

Q₂ – количество тепла принятого менее нагретым теплоносителем.

Пусть массовый расход более нагретого теплоносителя составляет G₁, его энтальпия на входе в аппарат i_1н и на выходе из аппарата i_1к. Соответственно расход более холодного теплоносителя – G₂, его начальная энтальпия i_2н и конечная энтальпия i_2к. Тогда уравнение теплового баланса

(1)

Если теплообмен протекает без изменения агрегатного состояния теплоносителей, то энтальпии последних равны произведению теплоемкости на температуру:

Величины С_1н; С_1к и С_2н; С_2к представляют собой средние удельные теплоемкости более и менее нагретых теплоносителей в переделах изменения температур.

Если теплообмен протекает при изменении агрегатного состояния теплоносителя (конденсация пара, испарение жидкости и др.) или в процессе теплообмена протекают химические реакции, сопровождаемые тепловыми эффектами, то в тепловом балансе должно быть учтено тепло, выделяющееся при физическом или химическом превращении. Так, при конденсации насыщенного пара, являющегося греющим агентом, величина i_1н в уравнении (1) представляет собой энтальпию поступающего в аппарат пара, а i_1к - энтальпию удаляемого парового конденсата.

В случае использования перегретого пара его энтальпия i_1н складывается из тепла, отдаваемого паром при охлаждении от температуры t_n до температуры насыщения t_нас, тепла конденсации пара и тепла, выделяющегося при охлаждении конденсата.

(2)

где r – удельная теплота конденсации, дж/кг;

с_п и с_к – удельные теплоемкости пара и конденсата, дж/(кг град);

t_к – температура конденсата на выходе из аппарата.

При обогреве насыщенным паром, если конденсат не охлаждается, то есть t_к = t_n = t_нас, первый и третий члены правой части уравнения (2) из теплового баланса исключаются.

Произведение расхода теплоносителя G на его среднюю удельную теплоемкость С условно называется водяным эквивалентом W. Численное значение W определяет массу воды, которая по своей тепловой емкости эквивалентно количеству тепла, необходимому для нагревания данного теплоносителя на 1 ⁰С, при заданном его расходе. Поэтому если теплоемкости обменивающихся теплом жидкостей (С₁ и С₂) можно считать не зависящими от температуры, то уравнение теплового баланса (1) примет вид

(3)

или

(4)

4.3 Основное уравнение теплопередачи

Общая кинетическая зависимость для процессов теплопередачи, выражающая связь между тепловым потоком Q и поверхностью теплообмена F представляет собой основное уравнение теплопередачи:

(1)

где К – коэффициент теплопередачи, определяющий среднюю скорость передачи тепла вдоль всей поверхности теплообмена;

– средняя разность температур между теплоносителями, определяющая среднюю движущую силу процесса теплопередачи, или температурный напор;

– время.

Согласно уравнению (1), количество тепла, передаваемое от более нагретого к более холодному теплоносителю, пропорционально поверхности теплообмена F, среднему температурному напору и времени .

Для непрерывных процессов теплообмена уравнение теплопередачи имеет вид

(2)

Из уравнения (1) вытекают единица измерения и физический смысл коэффициента теплопередачи. Так, при F = 1 м², = 1 град., = 1 сек.

Таким образом, коэффициент теплопередачи показывает, какое количество тепла (дж) переходит в 1 сек от более нагретого к более холодному теплоносителю через поверхность теплообмена 1 м² при средней разности температур между теплоносителями, равной 1 град.

4.4. Теплопередача при постоянных температурах теплоносителей через плоскую стенку.

Определим количество тепла, которое передается в единицу времени от более нагретой среды к менее нагретой среде, через разделяющую их стенку, причем t₁ > t₂.

Рис.4.1.

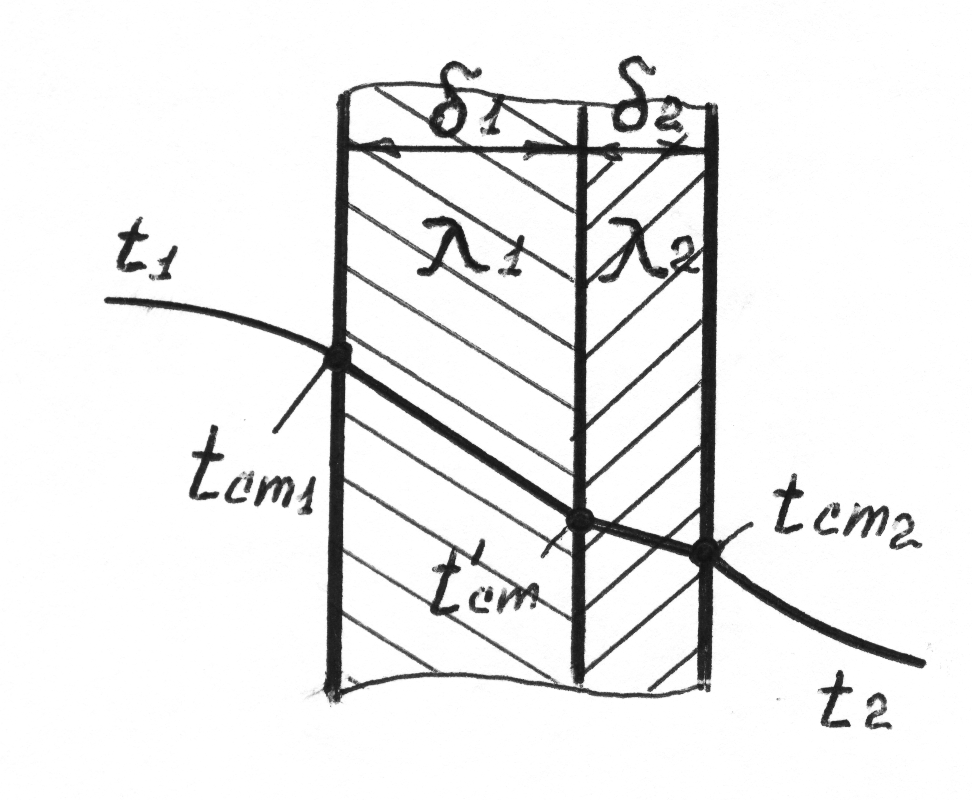
Стенка состоит из двух слоев с различной толщиной и теплопроводностью. Стенка толщиной имеет коэффициент теплопроводности , толщиной . Рабочая поверхность стенки F, процесс теплообмена установившийся. Следовательно, от более нагретой среды к стенке, сквозь стенку и от стенки к менее нагретой среде за одинаковое время передается одно и то же количество тепла.

Количество тепла, передаваемого за время от более нагретой среды к стенке, по уравнению теплопередачи (закон Ньютона) составляет

Количество тепла, проходящего путем теплопроводности через слои стенки (закон Фурье), равно

;

Количество тепла, отдаваемого стенкой менее нагретой среде

Полученные выражения могут быть представлены в виде

Сложив эти уравнения, получим

или

Первый множитель правой части этого уравнения называется коэффициентом теплопередачи

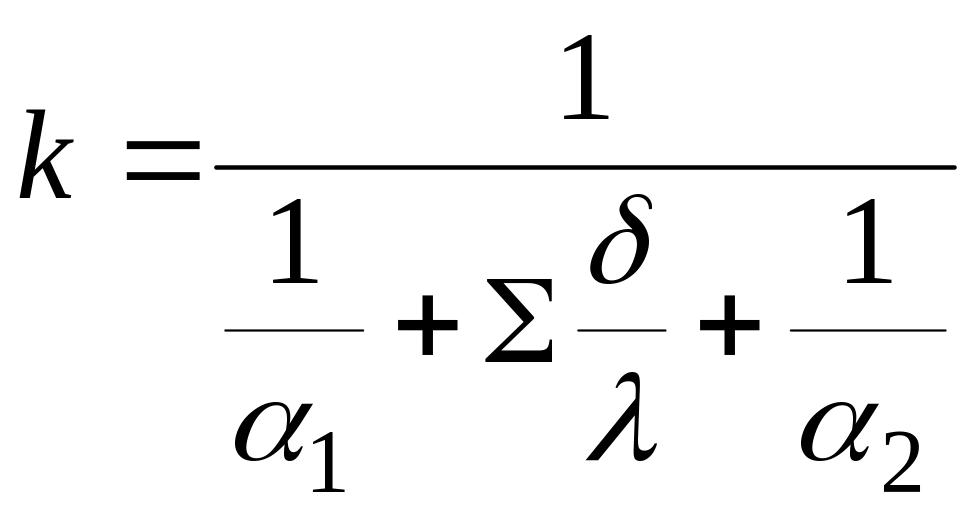
Соответственно уравнение теплопередачи для плоской стенки при постоянных температурах теплоносителей имеет вид

и для непрерывных процессов

Величина обратная к, называется общим термическим сопротивлением

где и - термическое сопротивление более нагретой и менее нагретой среды, соответственно;

- термическое сопротивление многослойной стенки.

Термические сопротивления отдельных слоев многослойной стенки могут значительно отличаться по величине, и одно из них, соответствующее слою с теплопроводностью, значительно более низкой, чем теплопроводность других слоев, является определяющим.

При теплопередаче через чистую металлическую стенку (без загрязнений и тепловой изоляции) термическое сопротивление стенки невелико и в первом приближении им можно пренебречь, приняв

.

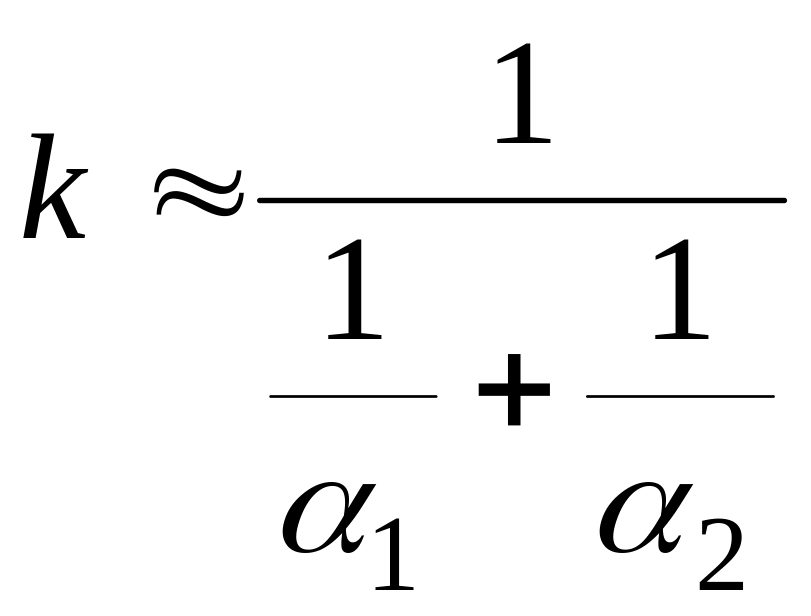Если значения коэффициентов теплоотдачи и значительно отличаются друг от друга, например , то 1/ во много раз больше 1/ и величина к практически определяется значением . В этом случае

.