99. Принципы построения САУ: разомкнутые и замкнутые системы, управление по возмущению, управление по отклонению, комбинированное управление. Классификация САУ.

В зависимости от схемы передачи сигналов различают следующие принципы построения САУ:

Е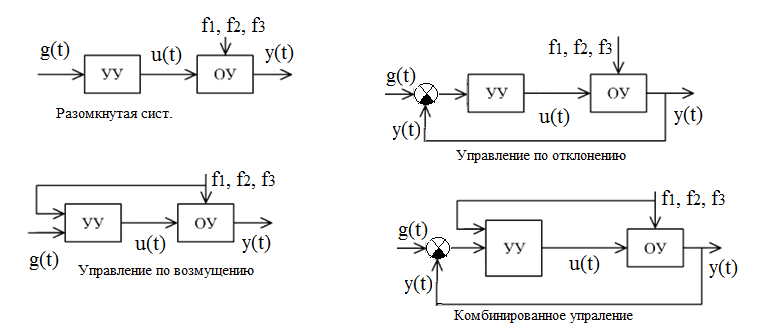 сли информация по выходной величине не используется, то система разомкнутая: выходная величина y(t) зависит от управляющего воздействия u(t), поступающего с Устройства Управления (УУ).

На вход УУ поступает задающее воздействие g(t). Величины f_i , приводящие к отклонению величины y(t) от заданного значения называются возмущающими воздействиями.

Задача САУ – обеспечение постоянства или изменение по заданному закону выходной величины. Для выполнения задачи используются принципы:

1. У правление по возмущению (Принцип компенсации возмущения).

Принцип: измеряется возмущение и с помощью УУ на объект создается воздействие, компенсирующее вредное влияние возмущения. f1 (контролируемое) называют главным возмущением.

Достоинства («+»): высокое быстродействие, т.к. управляющее воздействие u(t) создается одновременно с возникновением возмущения.

Недостатки («-»): 1) Устраняется влияние только измеряемого возмущения. 2) Точная компенсация требует настройки регулятора и с течением времени нарушается, т.к. изменяются параметры системы.

Поэтому регулирование по возмущению самостоятельно применяется редко.

2. Управление по отклонению (по ошибке).

И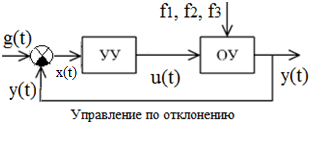 дея состоит в том, чтобы найти разность x(t)=g(t)-y(t) между задающим воздействием и выходной величиной, и по x(t) создать управляющее воздействие u(t) на Объект Управления (ОУ). Величина x(t) – ошибка регулирования.

∆ y=- x(t)= y(t)-g(t) – отклонение регулируемой величины от заданного значения. УУ вырабатывает воздействие, чтобы уменьшить величину ошибки.

«+»: 1) Устраняет влияние любого возмущения, действующего на объект. 2) Нет жестких требований к стабильности параметра УУ, т.к. изменение параметра приводит к ошибке x(t), которая затем устраняется УУ.

«-»: 1) Управляющее воздействие u(t) вырабатывается после появления ошибки, т.е. в первый момент ошибка может быть значительна. 2) Наличие замкнутого контура может приводить к неустойчивой работе (колебаниям).

Система по возмущению – разомкнутая система.

Система по отклонению – замкнутая.

3. Комбинированное управление.

О дновременно используется управление по возмущению и по ошибке.

В первый момент при возмущении f1 вырабатывается управляющее воздействие по принципу компенсации и если ошибка ≠0, то дополнительно вырабатывается воздействие по ошибке. Достоинства 1-го и 2-го принципа объединяются.

Системы 2-го и 3-го замкнутого типа называются системы с обратной связью (ОС).

ОС – подача сигнала с выхода на ее вход. Если сигнал обратной связи вычитается (-y(t)), то это отрицательная ОС. Иначе – положительная (ПОС).

При регулировании по ошибке используется ООС.

Классификация сау.

По наличию обратной связи: разомкнутые // замкнутые.

По числу управляемых величин: одномерные // многомерные.

По степени использования вычислительной техники: системы без вычислительных устройств // с использованием микропроцессоров // системы с программируемым компьютерным управлением.

По назначению: системы автоматического регулирования (САР) // системы с произвольным законом управления (оптимальные // самонастраивающиеся // адаптивные).

САР: системы стабилизации (задающее воздействие g(t)=const) // системы программного регулирования (g(t)=var – известный закон) // следящие системы (g(t)=var – неизвестная функция).

По способу математического описания и характеру протекания процессов:

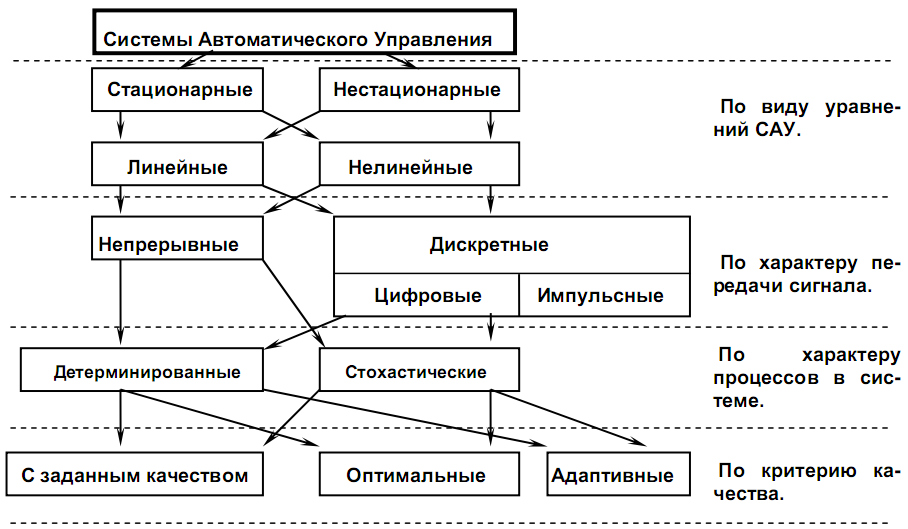
По виду уравнений САУ: стационарные///нестационарные; линейные///нелинейные.

По характеру передачи сигнала: непрерывные///дискретные (цифровые//импульсные).

По характеру процессов в системе: детерминированные///стохастические.

По критерию качества: оптимальные/// адаптивные///с заданным качеством.

100 Уравнения линейных систем в изображениях по Лапласу. Передаточная функция по Лапласу. Связь передаточной функции по Лапласу с операторной передаточной функцией.

В ТАУ для описания свойств линейных звеньев широко используются передаточные функции. Существуют два вида передаточных функций:

– операторная передаточная функция W(p);

– передаточная функция по Лапласу.

Суть преобразований Лапласа состоит в переходе от функции времени к функции комплексной переменной , где s=c+jω.

Преобразование Лапласа осуществляется по следующим формулам:

прямое преобразование:

обратное преобразование: , при ,

Рассмотрим основные свойства преобразования Лапласа

1. Линейность:

, ; .

2. Изображение производной:

;

Для производной любого порядка

.Если все начальные условия нулевые, т.е. 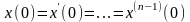, то .

3. Изображение интеграла:

.

4. Свойства для пределов оригинала и изображения:

, (теорема о начальном значении оригинала);

, (теорема о конечном значении оригинала).

Используется для нахождения начального и конечного положения, если знаем изображение.

5. Изображения типовых функций времени:

а) единичная ступенчатая функция

;

б) единичная импульсная функция (функция Дирака)

; . .

в) функция запаздывания

, τ – время запаздывания; например, если x(t)=A·sin(ωt), то

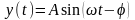, где φ=ωτ.

Имеем: .

Пусть теперь имеется динамическое звено, описываемое обыкновен­ным линейным дифференциальным уравнением

,

или в операторной форме при p=d/dt

, (1) где ,

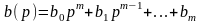
Согласно уравнению (1) операторная передаточная функция звена

.

Применяя к этому дифференциальному уравнению преобразование Лапласа, получим: , или при нулевых начальных условиях

,

где , .

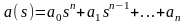Отношение называется передаточной функцией динамического звена по Лапласу.