И. Э. Симонова, И. А. Тарасова

Б. В. Симонов, А. А. Ермакова

Начала

аналитической геометрии

М ИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

И. Э. СИМОНОВА, И. А. ТАРАСОВА

Б. В. СИМОНОВ, А. А. ЕРМАКОВА

НАЧАЛА

АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

Учебное пособие

Волгоград

2010

У ДК 514.12(075)

Рецензенты:

зав. кафедрой «Математический анализ и теория функций»

Волгоградского государственного университета д-р физ.-мат. наук А. А. Клячин;

д-р техн. наук, профессор кафедры «Математический анализ»

Волгоградского государственного педагогического университета

Б. А. Жуков

Издается по решению редакционно-издательского совета

Волгоградского государственного технического университета

Симонова, И. Э.

Начала аналитической геометрии : учеб. пособие / И. Э. Симонова, И. А. Тарасова, Б. В. Симонов, А. А. Ермакова. – Волгоград : ИУНЛ ВолгГТУ, 2010. – 48 с.

ISBN 978–5–9948–0610–4

Приведены основные понятия по разделу «Аналитическая геометрия» кур-са математики; многочисленные примеры и графические иллюстрации, а также справочные материалы. Показаны возможности использования ППП Mathcad. Представлены методические материалы по контролю знаний студентов; даны 25 вариантов заданий для самостоятельной работы.

Предназначено для студентов первого курса всех специальностей и всех форм обучения.

Ил. 28. Табл. 5. Библиогр.: 7 назв.

ISBN 978–5–9948–0610–4 © Волгоградский государственный

технический университет, 2010

Введение

Основной задачей аналитической геометрии является исследование геометрических форм с помощью алгебраического анализа.

Идея аналитической геометрии восходит к работам философа и математика Р. Декарта. В 17 в. он ввел первую (декартову) систему координат на плоскости (см. п. 1.1).

Метод координат, дающий возможность однозначного описания положения точек при помощи чисел, называемых их координатами, лег в основу аналитической геометрии.

Аналитическая геометрия устанавливает, каким образом геометрические свойства линий, поверхностей и других геометрических объектов отражаются на алгебраических соотношениях, задающих координаты точек этих объектов. Исследованию этого вопроса посвящены пп. 1.2–1.7.

В свою очередь, алгебраические зависимости (уравнения, неравенства, системы) можно интерпретировать как геометрические объекты, получая наглядные представления чисто алгебраических задач.

Методы аналитической геометрии широко применяеются в естествознании, технике, экономике. При изучении аналитической геометрии предполагается, что студенты уже изучили раздел «Векторная алгебра» курса математики.

В первой части пособия приводятся основные теоретические положения и решения стандартных задач.

Во второй части представлены учебно-методические материалы по контролю заданий. Эти материалы могут быть использованы студентами при выполнении ОргСРС, подготовке к контрольной работе «Аналитическая геометрия» и подготовке к экзамену.

1. Стандартные задачи и основные положения теории

1. Метод координат. Уравнения линий и поверхностей

Д екартовая прямоугольная система координат (СК) на плоскости Охуz задается с помощью точки О (начала координат) и парой выходящих из нее ортонормированных векторов , , образующих декартов базис. Каждой точке М плоскости Оху соответствует пара ее координат (х_M у_M) (см.рис.1.1).

Д екартовая СК в пространстве Охуz задается с помощью точки О начала координат и ортонормированного базиса ( , , ). Положение точки М определяется координатами (х_M,у_M,z_M), являющимися ее проекциями на координатные оси Оx, Оy, Oz (см. рис. 1.2). Заметим, что длина векторов , , равна единице масштаба.

В торая СК на плоскости – полярная, она задается точкой О (полюсом) и полярной осью – выходящим из нее лучом ОЕ с выбранной единицей масштаба. Положение точки М задается парой координат – полярным радиусом ρ_М=ОМ и полярным углом φ_М (см.рис.1.3).

Формулы перехода из полярной СК в декар-товую и обратно следуют из соотношений меж-ду сторонами и углом в треугольнике ОМx_М:

х_М = ρ_М ∙ cosφ;

у_M = ρ_М ∙ sinφ;

ρ_M =

Угол φ определяется двумя условиями:

sin φ= у_M /ρ_M ; cos φ= х_М /ρ_M ;

Ц илиндрическая СК объединяет эти две СК: в трехмерном пространстве на плоскости Оху вводятся полярные координаты (ρ,φ), а по оси Оz откладывается проекция луча ОМ на эту ось. Тогда положение точки М в пространстве определяется тремя координатами: М=М(ρ_М, φ_М, z_M)

В сферической СК точка М задается координатами М(r_M, φ_М, θ_M ), где r_M = |OM|, а в качестве третьей координаты берется угол θ_M между радиус-вектором и осью Оz а (см. рис. 1.5)

Успех решения многих прикладных задач физики (в т.ч. механики), химии, техники в значительной степени определяется выбором подходящей для данной задачи системы координат

Способы задания линий и поверхностей

В декартовой СК на плоскости существует три основных способа задания линий.

Первый из них – «явный», с помощью функции y = y(x), x[a,b];

В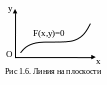 торой, более общий способ – «неявный», с помощью уравнения F(x,y)=0, если этому уравнению удовлетворяют те и только те точки, которые принадлежат линии L

Третий способ – «параметрический», когда координаты (x,y) точек линии L задаются уравнениями х=х(t), y=y(t), t[t₁,t₂]. Параметр t часто интерпретируется как время.

В полярной СК явное уравнение линии имеет вид:

ρ=ρ(φ), φ [ , ], неявное – F(ρ,φ)=0.

Пример 1.1 Окружность радиуса R с центром в точке О может быть задана в декартовой СК:

1. явно: с помощью пары функций y = ±, x 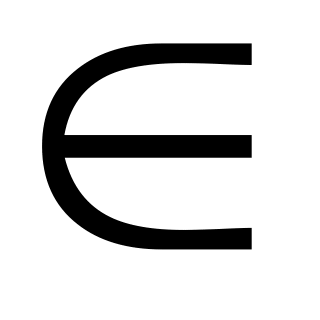[-R,R];

2. неявно: уравнением x²+y²=R²;

3 ) параметрически: x=Rcosφ

y=Rsinφ , φ [0,2 ]

В полярной СК уравнение этой же окружности =R.

Уравнение поверхности в пространстве с введенной в нем декартовой СК может быть задано неявно с помощью уравнения F(x,y,z)=0, если ему удовлетворяют те и только те точки М(x,y,z), которые лежат на поверхности . В такой форме принято представлять, например, уравнения поверхностей второго порядка (см. п. 1.7).

Аналогично задаются поверхности в цилиндрической и сферической СК.

Л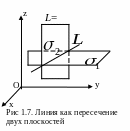 иния L в пространстве может быть задана как линия пересечения двух поверхностей: L= (рис. 1.7).

Аналитически этому соответствует решение системы уравнений

F ₁(x,y,z)=0,

F₂(x,y,z)=0,

где F₁(x,y,z)=0 и F₂(x,y,z)=0 – уравнения поверхностей и в декартовой СК.

Второй способ – параметрическое задание линии системой трех уравнений:

x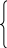 =x(t)

y=y(t) t [t₁,t₂]

z=z(t)

В разных СК одна и та же линия или поверхность задается разными формулами. Подтверждением этому служит пример 1.1.

С другой стороны, одна и та же формула порождает разные геометрические формы и разные, по сути, виды движения в зависимости от используемой СК. Это иллюстрируют примеры 1.2, 1.3.

Три основных типа движения, рассматриваемых в механике - поступательное, колебательное и вращательное.

Пример 1.2. В декартовой СК с координатами (t,y) прямолинейное движение задается линейным уравнением y=a+bt или, в частном случае, уравнением y=t.

Н о движения, описываемые одной и той же формулой линейной зависимости, в декартовой, полярной и цилиндрической СК совершенно различны.

В декартовой СК уравнение y=at+b описывает прямолинейное движение. В полярной СК при t=φ, a>0 уравнение r=at+b описывает движение по раскручивающийся спирали. В цилиндрической СК получаем снова спираль (рис. 1.8).

В частном случае, когда a=0, b=1, получаем прямую y=1 в декартовой СК и окружность r=1 в полярной СК.

Пример 1.3. В декартовой СК колебательное движение задается уравнением y=sin t или более общим уравнением Acos (at+b),где t - время, А – амплитуда, а – частота колебаний, b – фаза.

Д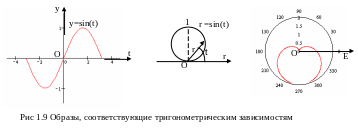 вижение, описываемое формулой y=sint в декартовой СК – это колебательное движение с периодом 2. В полярной СК формула r=sint (при t=φ) задает движение по окружности. Взяв формулу y=1-sint, в декартовой СК снова получим колебательное движение, в полярной - кардиоиду (рис 1.9).