2.3.4 Суммарное число зубьев и угол наклона

Минимальный угол наклона зубьев косозубых колес [1, стр. 21]

β_min = arcsin(4m/b₂);

β_min = arcsin(4∙4.0/71) = 13.02^o.

Суммарное число зубьев

z_s = 2a_wcosβ_min/m = 109,6.

Полученное значение z_s округляют в меньшую сторону до целого числа и определяют действительное значение угла β наклона зуба:

β = arccos[z_sm/(2a_w)].

z_s = 117;

β = arccos[109 ∙ 4.0/(2∙225)] = 14,3^o.

Справочно: для косозубых колес β = 8...20^o, для шевронных - β = 25...40^o.

2.3.5 Число зубьев шестерни и колеса

Число зубьев шестерни [1, стр. 21]

z₁ = z_s / (u   1) ≥ z_1min;

z₁ = 109 / (2.24 + 1) = 33.64

Значение z₁ округляют в ближайшую сторону до целого числа. [1, стр. 21]

z₁ = 34.

Число зубьев колеса внешнего зацепления z₂ = z_s - z₁.

z₂ = 109 - 34 = 75.

2.3.6 Фактическое передаточное число

u_ф = z₂/z₁ = 75/34 = 2.21.

Фактические значения передаточных чисел не должны отличаться от номинальных более чем на: 3% - для одноступенчатых, 4% - для двухступенчатых и 5% - для многоступенчатых редукторов.[1, стр. 22]

Отклонение от номинального передаточного числа

Δ = (u - u_ф)/u = 1,3 %.

2.3.7 Диаметры колес

Рис. 6 [1, рис. 2.5, стр. 22]

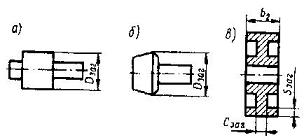
Рис. 7 [1, рис. 2.6, стр. 22]

Делительные диаметры d [1, стр. 22]:

шестерни.........................................d₁ = z₁m/cosβ;

колеса внешнего зацепления............d₂ = 2a_w - d₁;

колеса внутреннего зацепления........d₂ = 2a_w + d₁;

d₁ = 34 ∙ 4.0 / cos14,3^o = 131,78 мм;

d₂ = 2 ∙ 225 - 131.78 = 318.22 мм.

Диаметры d_a и d_f окружностей вершин и впадин зубьев колес внешнего зацепления [1, стр. 22]:

d_a1 = d₁ + 2m;

d_f1 = d₁ - 2(1,25 - x₁)m;

d_a2 = d₂ + 2m;

d_f2 = d₂ - 2(1,25 - x₂)m;

где x₁ и x₂ - коэффициенты смещения у шестерни и колеса; y = -(a_w - a)/m - коэффициент воспринимаемого смещения; a - делительное межосевое расстояние: a = 0,5m(z₂   z₁).

a = 0.5 ∙ 4.0 ∙ (75+34) = 218 мм;

y = -(225 - 218)/4.0 = -1.5;

d_a1 = 131.7 + 2 ∙ 4.0 = 139,78 мм;

d_f1 = 131.78 - 2 ∙ 1,25 ∙ 4.0 = 121.78 мм;

d_a2 = 318.22 + 2 ∙ 4.0 = 326,2 мм;

d_f2 = 318,22 - 2 ∙ 1,25 ∙ 4.0 = 308.21 мм;

2.3.8 Размеры заготовок

Чтобы получить при термической обработке принятые для расчета механические характеристики материала колес, требуется, чтобы размеры D_заг, C_заг, S_заг заготовок колес не превышали предельно допустимых значений D_пр, S_пр (табл. 1 [1, табл. 2.1, стр. 11]) [1, стр. 22]:

D_заг ≤ D_пр; C_заг ≤ C_пр; S_заг ≤ S_пр.

Значения D_заг, C_заг, S_заг (мм) вычисляются по формулам: для цилиндрической шестерни (рис. 7, а) D_заг = d_a + 6 мм; для колеса с выточками (рис. 7, в) C_заг = 0,5b₂ и S_заг =8m; для колеса без выточек (рис. 6) S_заг = b₂ + 4 мм.

D_заг1 = 139.78 + 6 мм = 145.78мм;

D_заг2 = 326.2 + 6 мм = 332.2 мм;

S_заг2 = 71+ 4 мм = 75 мм.

2.3.9 Проверка на выносливость по контактным напряжениям и напряжениям изгиба тихоходной ступени редуктора.

Условие контактной прочности передачи имеет вид _HP.

Контактные напряжения определяются по формуле:

= ,

где = 8400 для прямозубых передач,

К_Н - коэффициент контактной нагрузки.

Коэффициент контактной нагрузки определяется по формуле:

К_Н = K_Hα K_Hβ К_НV,

где K_Hα - коэффициент неравномерности распределения нагрузки между зубьями,

K_Hβ – коэффициент неравномерности распределения нагрузки по ширине колеса,

К_НV – динамический коэффициент.

Коэффициенты К_НV и K_Hα уточняем по таблицам после определения размеров передачи и фактической окружной скорости:

, где A=0.15 – для прямозубых передач;

При для определения K_w используем выражение:

.

Коэффициент неравномерности распределения нагрузки по ширине колеса:

,

- коэффициент неравномерности распределения нагрузки в начальный период работы.

Для определения вычислим коэффициент ширины венца по диаметру:

По значению определим методом линейной интерполяции c.14(см. табл.9.1)[2], , тогда .

Динамический коэффициент определим методом линейной интерполяции по табл. 10.1, К_НV=1.05.

Окончательно найдём К_Н:

К_Н =1,09∙1,02004∙1,05=1,17.

Таким образом,

Допускается перегрузка по контактным напряжениям не более 5%, рекомендуемая недогрузка до 15%. Расчет перегрузки или недогрузки выполним по формуле

Определяем недогрузку

Напряжения изгиба в зубе шестерни:

Коэффициенты формы зуба : - эквивалентное число зубьев.

- коэффициент, учитывающий влияние угла наклона зуба на его прочность:

Коэффициент торцевого перекрытия:

Коэффициент, учитывающий перекрытие зубьев

Коэффициент нагрузки при изгибе

Для определения составляющих коэффициентов используем следующие зависимости:

Тогда:

Напряжение изгиба в зубьях колеса: