4.3.8. Уравнение Михаэлиса–Ментен

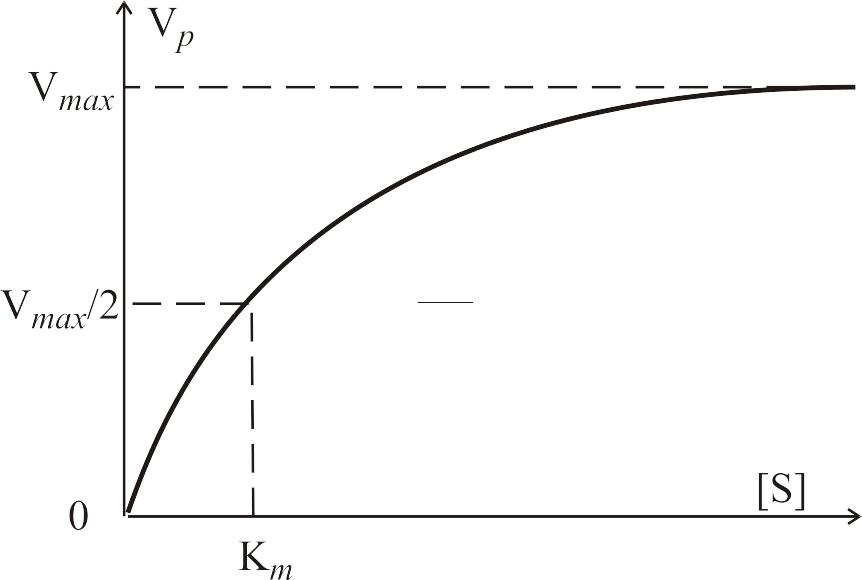
Максимальная скорость характеризует эффективность ферментативной реакции. Наличие предельной скорости объясняется тем, что при высоких концентрациях субстрата [S] активные центры практически всех молекул фермента оказываются насыщенными. Новые комплексы могут образоваться лишь через время, необходимое для диссоциации уже имеющихся фермент – субстратных комплексов. Уравнение (4.32) в форме

(4.34)

носит название уравнения Михаэлиса–Ментен. Зависимость (4.34) скорости ферментативной реакции Михаэлиса–Ментен (4.21) от концентрации субстрата [S] представлена на рис. 4–7.

Рис. 4–7. Зависимость скорости каталитической реакции (4.21) от концентрации субстрата S, F – фермент, P – продукт

Константа Михаэлиса численно равна той концентрации субстрата [S], при которой скорость достигает половины от максимальной величины : . Константа Михаэлиса характеризует сродство фермента к субстрату. Чем меньше , тем больше скорость V_max, выше сродство, то есть наблюдается более быстрый рост скорости реакции с увеличением концентрации субстрата , чем при больших значениях константы .

По такой схеме, когда фермент может находиться в двух состояниях (свободном F и в виде комплекса FS) и имеется только один субстрат S, идет реакция гидролиза АТФ. Например, мышечный белок миозин (фермент) катализирует переход избытка химической энергии пирофосфатной связи АТФ в механическую энергию мышечного сокращения.

Зависимость от температуры

Скорость реакции зависит от температуры. С повышением температуры скорость реакции возрастает, так как увеличивается конформационная подвижность и скорость образования фермент – субстратного комплекса. Однако при достаточно высоких температурах, вследствие разрушения (денатурации) вторичной и третичной структур фермента, скорость ферментативной реакции снова уменьшается. Она также мала и при температурах вблизи замерзания, когда ферменты инактивируются. Поэтому возможно достаточно длительное хранение замороженных продуктов, в которых значительно снижается рост и размножение микроорганизмов, так как происходит инактивация их пищеварительных ферментов.

§4.4. Многостадийная модель ферментативных реакций

Для бимолекулярных реакций, в которых участвуют субстраты двух типов А и В:

А + В  С + D,

где С и D – продукты реакции, простейший двухстадийный процесс реакции может быть осуществлен по схеме:

А + F  АF и АF + В  F + С + D.

В общем случае снижение потенциальных барьеров связано с тем, что каталитические реакции протекают по новому механизму, складывающемуся из последовательности элементарных реакций с меньшими значениями энергии активации, чем при не каталитических реакциях. Кроме того, происходит заимствование части энергии при многоточечном связывании. При этом в процессе реакции образуется большое число лабильных соединений Х_n, времена жизни которых варьируются от нано- до миллисекунд. Формула каталитической реакции в этом случае имеет вид

,

где k_n – константы скоростей отдельных промежуточных элементарных стадий реакции.

Появление лабильных соединений Х_n является следствием последовательных конформационных изменений в фермент – субстратном комплексе, вызванных первичным изменением электронного состояния активного центра фермента. При изменении электронного состояния в течение времени , возбуждаются колебательные степени свободы лишь небольшого числа выделенных химических связей субстрата и функциональных групп фермента, не затрагивающие основную часть белковой глобулы. Возникающее конформационно неравновесное состояние значительно более медленно релаксирует к равновесному исходному состоянию. В процессе релаксации поэтапно синтезируются промежуточные соединения Х_n. При этом ось ферментативной реакции и ось конформационной релаксации совпадают.