6.3 Метод Фур’є для розв’язування задачі теплопровідності

Розглянемо задачу теплопровідності у скінченному стержні довжиною l. нехай його кінці відповідають точкам х=0 та х=l на осі Ох. Враховуючи специфіку метода Фур’є, розглянемо ряд задач з однорідними крайовими умовами.

1) Знайти розподіл температур в стержні, на кінцях якого весь час підтримується нульова температура, а початковий розподіл задається функцією

Поставимо задачу:

,

П.У. К.У. (6.19)

Для неперервності U(х; t) в точках (0; 0) і (l; 0) необхідно вимагати, щоб φ(0)=φ(l)=0. Також припускаємо, що функцію можна розкласти по синусах кратних дуг на проміжку . Згідно методу Фур’є ненульові розв’язки рівняння, що задовольняють умови (6.19), шукаємо у вигляді добутку двох функцій:

Підставляючи цю функцію у рівняння теплопровідності, отримаємо:

або

Останній факт було досліджено при розв’язуванні задач про коливання. Таким чином, рівняння теплопровідності розпадається на два звичайних диференціальних рівняння:

, (І)

(ІІ)

Розглянемо спочатку перше рівняння і знайдемо функцію Оскільки розв’язки характеристичного рівняння є комплексно спряженими то шукана функція набуває вигляду

Для знаходження невідомих сталих, використовуємо крайові умови, записані для функції

К.У.

Звідси:

Очевидно, що (інакше отримаємо тривіальний розв’язок). Тоді:

Отже, маємо:

, (6.20)

Тепер з рівняння (ІІ) знайдемо функцію Це диференціальне рівняння першого порядку з відокремлюваними змінними:

, тоді

Враховуючи, що , остаточно маємо:

, (6.21)

Таким чином, знайдено частинні розв’язки рівняння теплопровідності:

Оскільки рівняння теплопровідності є лінійним та однорідним, то його загальний розв’язок можна знайти, як суму частинних розв’язків:

або, позначивши , запишемо:

(6.22)

Для визначення коефіцієнта скористаємося початковою умовою:

П.У.

Звідси:

Для функції отримано розклад в ряд Фур’є за синусами в інтервалі з коефіцієнтами розкладу . Тоді згідно формул Фур’є:

(6.23)

Таким чином, розв’язок задачі про поширення тепла у стержні, на кінцях якого підтримується нульова температура, а початковий розподіл температур задається функцією шукається за формулами (6.22), (6.23).

Зауваження

Розглянемо випадок, коли на кінцях стержня задається ненульова температура. Тоді задача має наступну постановку:

, ,

П.У. К.У. (6.24)

Тут та – сталі температури відповідно на кінцях х=0 та x=l.

У цій задачі з неоднорідними граничними умовами достатньо зробити підстановку:

(6.25)

яка зведе її до попередньої задачі відносно функції Цю процедуру пропонується виконати студентам самостійно.

Розглянемо ще одну задачу про поширення тепла у стержні.

2) Знайти розподіл температур в стержні, на одному кінці якого весь час підтримується нульова температура, а другий кінець теплоізольвано при довільній початковій умові.

Поставимо задачу:

, ,

П.У. U(x,0)=φ(x), К.У. (6.26)

Зазначимо, що тут не суттєво, який кінець теплоізольовано. Як бачимо, крайові умови однорідні. Розв’яжемо цю задачу за методом Фур’є, згідно якого

(6.27)

Тоді рівняння теплопровідності:

або

Розглянемо рівняння

,

розв’язок якого

Сталі А та В шукаємо із крайових умов:

К.У.

Розпишемо граничні умови:

Очевидно, що тоді

Звідси ,

Отже,

. (6.28)

Розв’яжемо друге рівняння для функції , що одержується з рівняння теплопровідності:

.

.

Розв’язок цього рівняння:

.

Враховуючи, що , , отримаємо

. (6.29)

Отже, маємо і розв’язок даної задачі шукаємо у вигляді:

Поклавши , остаточно будемо мати:

. (6.30)

Коефіцієнти визначаються із початкової умови, як у попередній задачі:

(6.31)

Отже, формули (6.30) і (6.31) дають розв’язок даної задачі.

3) Розв’язати задачу про поширення тепла в стержні, на одному кінці якого стала температура U₀, а другий – теплоізольований.

Поставимо задачу:

, ,

П.У. U(x,0)=φ(x), К.У. (6.32)

За методом Фур’є крайові умови мають бути нульовими. Тому проведемо заміну

Рівняння теплопровідності:

,

К.У. (6.33)

П.У.

За методом Фур’є отримаємо

(6.34)

де

Отже, остаточно маємо:

Приклад 6.2 Розв’язати задачу про поширення тепла у стержні довжиною l, на кінцях якого весь час підтримується нульова температура, а початковий розподіл температур задається функцією

• Поставимо задачу:

, ,

П.У. К.У.

Згідно з методом Фур’є ця задача має розв’язок:

де

Як відомо, система власних функцій є ортогональною на проміжку , тобто

коли , і не дорівнює нулю, коли .

Таким чином, усі коефіцієнти проте коефіцієнт Знайдемо його:

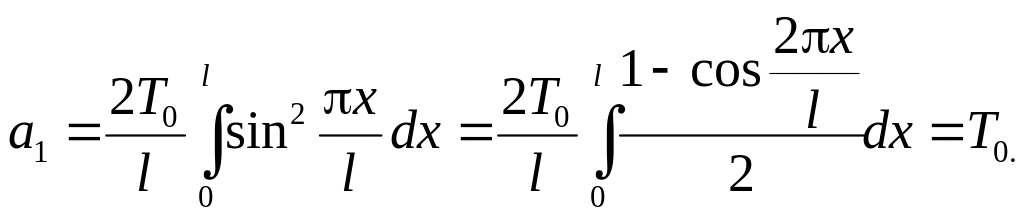
Тоді розв’язок задачі запишемо так