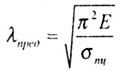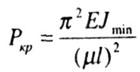- •1. Дать определение расчетной схемы.
- •2. Какие силы называются внешними и внутренними?
- •3. Какой прием используется для выявления внутренних сил?
- •8. Что такое полосы скольжения?
- •9. От чего зависит система расположения атомов в кристаллической
- •28. В каких точках возникают максимальные нормальные напряже-
- •29. Как вычислить касательные напряжения, возникающие в про-
- •30. Для чего служат теории прочности?
- •31. На каких предположениях основаны первая, вторая, третья и чет-
- •Вторая теория прочности
- •Третья теория прочности
- •Четвертая теория прочности — энергетическая.
- •32. Какие теории прочности пригодны для расчета пластичных мате-
- •33. Какие теории прочности надо считать наиболее надежными?
- •34. Почему при выделении элемента из стенки сосуда показаны лишь
- •35. Что называется интенсивностью равномерно распределенной на-
- •36. Что называется изгибающим моментом и поперечной силой в
- •Этапы метода сечений
- •Внутренние силы в методе сечений
- •Вычисление продольной и поперечных сил, крутящего и изгибающих моментов
- •37. Какая существует связь между изгибающим моментом, попереч-
- •42. Как в общем виде пишется формула Эйлера?
- •43. Что называется коэффициентом приведения длины?
- •44. Чему равен коэффициент приведения длины для четырех случаев
- •45. Какой момент инерции используют в формуле Эйлера? Почему?
- •46. Что называется гибкостью стержня?
- •47. Какова формула гибкости стержня?
- •48. Как рассчитывается стержень на продольный изгиб, если гиб-
- •49. От чего зависит коэффициент ?
- •50. Какой цикл напряжений называется симметричным?
42. Как в общем виде пишется формула Эйлера?
Для шарнирно закрепленного, центрально-сжатого стержня постоянного сечения (рис.8.2). I Формула Эйлера имеет вид: |
|
где Е - модуль продольной упругости материала стержня; |
Jmin - минимальный момент инерции поперечного сечения стержня. |
Для стержней с другими видами закрепления формулу Эйлера записывают в виде: |
|
где |
|
Выражение "приведенная длина" означает, что в формуле Эйлера с помощью коэффициента все случаи закрепления концов стержня можно привести к основному, шарнирному закреплению. |
Коэффициент приведения длины иногда можно оценить по числу полуволн n, по которым выпучится стержень, теряя устойчивость, а именно, можно принять |
|
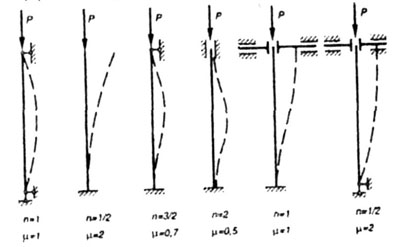
На рис. 8.2 показаны наиболее часто встречающиеся на практике случаи закрепления концов стержня и соответствующие им значения коэффициента |
|
Рис. 8.2 |
Формула
Эйлера применима только о пределах
выполнения закона Гука, когда критическое
напряжение |
|
в свое время полученной на основании закона Гука. |
Применимость формулы Эйлера можно определить, оценив гибкость стержня и сравнив эту гибкость с ее предельным значением. Гибкость стержня равна |
|
где |
|
|
Значение
предельной гибкости |
|
Предельная гибкость равна |
|
Так, для малоуглеродистой стали, если принять Е = 2x105 МПа, |
|
Для
повышения несущей способности
конструкций в них стремятся использовать
стержни возможно меньшей гибкости.
Так что расчет реальных конструкций
с гибкостью |
верхней границей значений гибкости реальных стержней. |
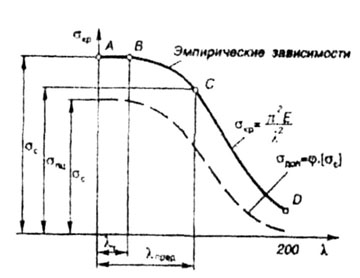
Следовательно, формула Эйлера для определения критического значения сжимающей силы в виде |
|
применима в случае, если гибкость стержня находится в пределах |
|
(кривая СД на рис. 8.3) |
|
Рис. 8.3 |
Для малоуглеродистой стали этот диапазон равен |
|
43. Что называется коэффициентом приведения длины?
где - приведенная длина стержня; |
- коэффициент приведения длины. |
Выражение "приведенная длина" означает, что в формуле Эйлера с помощью коэффициента все случаи закрепления концов стержня можно привести к основному, шарнирному закреплению. |
Коэффициент приведения длины иногда можно оценить по числу полуволн n, по которым выпучится стержень, теряя устойчивость, а именно, можно принять |
|
На рис. 8.2 показаны наиболее часто встречающиеся на практике случаи закрепления концов стержня и соответствующие им значения коэффициента |
|

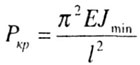
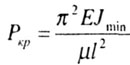


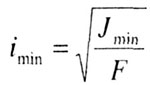 -
минимальный радиус инерции (геометрическая
характеристика сечения);
-
минимальный радиус инерции (геометрическая
характеристика сечения);