03_Дифференциаторы на ОУ

9

Лабораторная работа № 3

ИЗУЧЕНИЕ МЕТОДОВ ПОСТРОЕНИЯ ДИФФЕРЕНЦИАТОРОВ И ИХ ХАРАКТЕРИСТИК

Цель работы: изучение принципа работы и методов построения дифференциаторов, исследование характеристик дифференциаторов с помощью лабораторного макета.

1 КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Дифференциатором называется устройство, выходной сигнал U_вых которого пропорционален производной от его входного сигнала U_вх.

Простейшая схема дифференциатора, выполненная на ОУ, приведена на рис. 1.1.

Рис. 1.1 – Схема дифференциатора

Для идеального ОУ напряжение на конденсаторе U_c равно входному напряжению U_вх , а ток через сопротивление обратной связи R равен току через конденсатор C, т.е. ί_R = – ί_С. В этом случае выходное напряжение

U_вых = R·ί_R = – ί_С·R = – RC(dU_вх/dt).

Уменьшение реактивного сопротивления X_С с увеличением частоты f приводит к тому, что схема дифференциатора имеет высокий коэффициент усиления по отношению к высокочастотным составляющим на входе, даже если их частота лежит выше полосы частот полезного сигнала.

Рис. 1.2 – ЛАЧХ дифференциатора

Схема имеет тенденцию к потере устойчивости в той области частот, где частотная характеристика дифференциатора (имеющая подъём 6дБ/октава) пересекается с имеющей спад 6 дБ/октава характеристикой скорректированного усилителя (рис. 1.2).

Это означает, что частотная характеристика разомкнутого контура ОС имеет в некоторой части своего частотного диапазона спад 12 дБ/октава; при этих условиях вполне возможно самовозбуждение.

Чтобы избежать проявления только что описанных нежелательных свойств дифференциатора, принимаются меры по его динамической стабилизации (рис. 1.3).

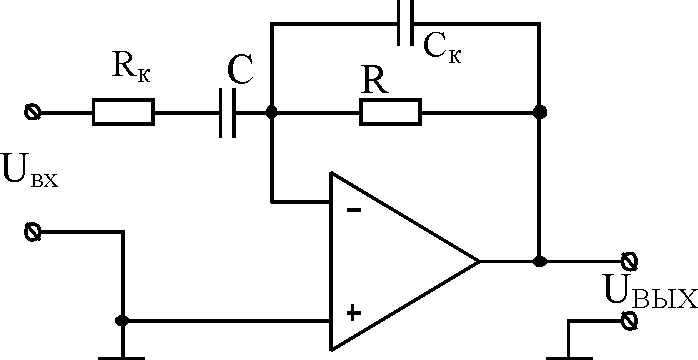
Рис. 1.3 – Схема скорректированного дифференциатора

Конденсатор С_К выбирается таким образом, чтобы участок характеристики со спадом 6 дБ/октава начинался на частоте более высокой, чем максимальная частота полезного дифференцируемого сигнала. Этот участок характеристики начинается на частоте равной f₂ = 1/2πRC_К (рис. 1.4).

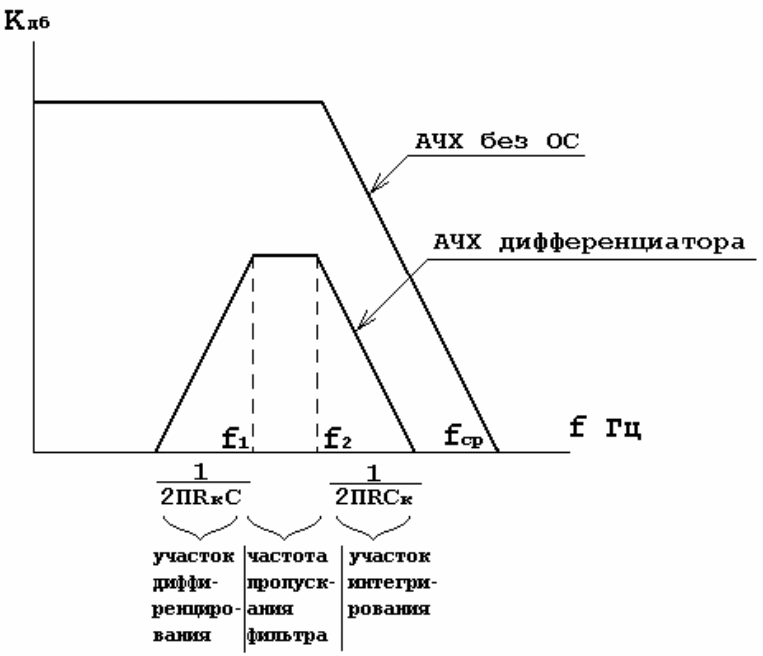
Рис. 1.4 – ЛАЧХ скорректированного дифференциатора

Сопротивление R_К ограничивает коэффициент усиления на высоких частотах, обеспечивает динамическую устойчивость и снижает емкостной ток схемы, отбираемый от источника сигнала. Добавление к схеме R_К приводит к появлению на частотной характеристике горизонтального участка и к прекращению дифференцирования на частотах, превышающих частоту f₁ = 1/2πR_КC.

Следует отметить, что в полосе частот от f до f₁ схема является устойчивым дифференциатором. Частоту f₁ следует задавать возможно более низкой при заданной полосе частот полезного сигнала и точности дифференцирования. Зависимость погрешности от частоты f₁ представлена в табл. 1.

_{Таблица 1 – Зависимость погрешности дифференциатора от f1}

f	0,01·f1	0,1·f1	0,33·f1	f1
ошибка в %	пренебрежимо мала	1	5	50

R_К и С_К часто выбирают так, чтобы R_К·C = R·C_К и f₁ = f₂.

2 ПРИМЕРЫ ДИФФЕРЕНЦИРОВАНИЯ

Пример 1: как будет выглядеть сигнал на выходе дифференциатора, если на его вход подать синусоидальное напряжение U_вх = U_оsin(t).

Решение:

выходное напряжение U_вых = – RC(dU_вх/dt) = – RCcos(t). Выходное напряжение изменяется по закону косинуса.

Пример 2: каким будет выходной сигнал, если на вход дифференциатора (R = 10 кОм, С = 0,1 мкФ) подать сигнал треугольной формы с частотой f = 1 кГц (рис. 2.5).

Решение:

рассмотрим U_вх как функцию времени. Так как этот сигнал является симметричной периодической волной, достаточно построить U_вых для одного полупериода. Выходное напряжение для следующего полупериода будет иметь ту же форму, но с противоположной полярностью.

Рис. 2.5 – Входной и выходной сигналы дифференциатора

Так как входное напряжение линейно возрастает до значения 2 В в течение 0,5 мс, то можно написать: U_вх = (2В/0,5мс)·t = (4·10³ В/с)·t, где t – время в секундах. Теперь найдём вид U_вых, пользуясь выражением:

U_вых = – RC·(dU_вх/dt).

U_вых = – RC·(d(4·10³) t/dt) = – RC·(4·10³ В/с) = –10·10³·0,1·10^-6·4·10³ = – 4 В.

Следовательно, выходной сигнал – это прямоугольная волна с амплитудой U_вых = 4 В и частотой f_вых = f_вх = 1 кГц. Выходной сигнал показан на рис. 2.5.

Таким образом, любому линейно изменяющемуся входному сигналу соответствует постоянный выходной сигнал, величина которого пропорциональна крутизне входного сигнала. Этот выходной сигнал остается постоянным в течение всего времени, пока входной сигнал сохраняет постоянный наклон.

Пример 3: каким будет выходной сигнал, если на вход дифференциатора (R = 10 кОм, С = 0,1 мкФ) подать прямоугольную волну с амплитудой 5 В и частотой следования 5 кГц, причем времена нарастания t_н и спада t_с импульсов равны 1 мкс (рис. 2.6).

Решение: входной сигнал, изображенный на рис. 2.6, следует разбить на части и дифференцировать раздельно.

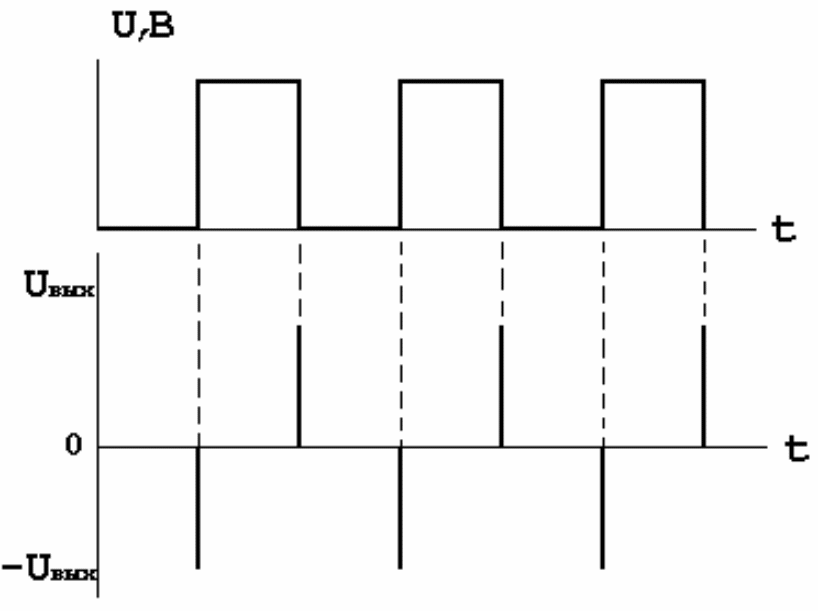
Рис. 2.6. – Входной и выходной сигналы дифференциатора

Участки входного сигнала, на которых его значение постоянно и равно 5 В или 0 В, не дают никакого напряжения на выходе дифференциатора, так как производная постоянной величины равна нулю. Участки нарастания и спада входных импульсов можно аппроксимировать наклонными прямыми. Т.к. t_н = t_c, то U_вх во время нарастания равно U_вх во время спада и противоположно ему по знаку.

Видно, что ненулевое выходное напряжение появляется только во время спада или нарастания входных импульсов. Для нахождения U_вых во время нарастания или спада надо сначала выразить эти участки входного сигнала как функции времени. Имеем U_{вх tн} = – U_{вх tc} = (5 В/1 мкс)·t = (5·10⁶ В/с)·t.

Теперь, используя выражение U_вых = – RC·(dU_вх/dt), получаем, что амплитуда выходного напряжения во время спада или нарастания входных импульсов

U_вых = RC(5·10⁶ В/с) = 10·10³·0,1·10^-6·5·10⁶ = 5·10³ В = 5 кВ.

Выходной сигнал при наличии реального ОУ будет состоять из двух импульсов противоположной полярности длительностью 1 мкс, амплитуда которых равна максимально возможному U_вых ОУ или напряжению ограничения, если в схеме использована схема ограничения.

Пример 4: какие значения R_К и С_К следовало бы использовать в примере 1, если максимальный коэффициент усиления равен 1000, максимальная частота дифференцируемого сигнала равна 10 кГц при допустимой ошибке 1%.

Решение:

при погрешности 1% максимальная рабочая частота должна быть равна:

f_max = (0,1) 1/(2π·R_КС).

Т.к. нас интересует только дифференцирование, полагаем:

1/2π·R_КС = 1/2π·RС_К = f_max /0,1 = 10·(10 кГц) = 100 кГц.

Максимальный допустимый коэффициент усиления К ≈ R/R_К, поэтому

R_К = R/1000 = 100 Ом.

С_К определяется из соотношения R_КС = RС_К, таким образом, С_К = R_КС/R = 0,001 мкФ.

3 ПОДГОТОВКА К ПРОВЕДЕНИЮ ИССЛЕДОВАНИЙ

1. Представить преподавателю результаты расчетов и моделирования.

2. Подобрать все необходимые для макетирования компоненты (после окончания работы компоненты возвращаются на место).

3. Собрать схему путем подключения соответствующих компонентов к контактным клеммам макета.

4. Проверить все соединения и после этого показать преподавателю.

ВНИМАНИЕ: включать питание и приборы можно только после проверки схемы преподавателем и получения разрешения!

После того, как монтаж проверен и получено разрешение, можно приступать к исследованиям.

5. Все измерения проводить относительно "земли". Сопротивление нагрузки не должно быть менее 2 кОм, в противном случае ОУ может выйти из строя. Отключать источник входного сигнала до того, как будет выключено питание. В противном случае ОУ может выйти из строя.

4 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

4.1 Собрать схему дифференциатора, представленную на рис. 4.1.

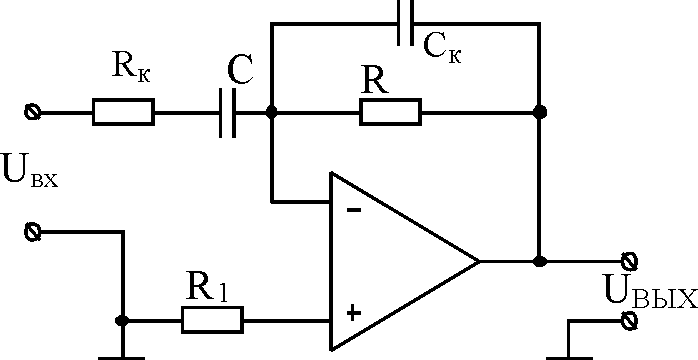
Рис. 4.1. – Схема скорректированного дифференциатора

Выбрать следующие номиналы компонентов:

R = 2 кОм, С = 0,1 мкФ,

R_К = 120 Ом, 300 Ом, С_К = 0,01 мкФ,

R₁ = 10 кОм,

4.2 Включить осциллограф С8-39 и комплекс КУЛ-1. Подать напряжение питания на лабораторный макет от КУЛ-1 (использовать выходы +12В и -12В).

4.3 Снять амплитудно-частотные характеристики дифференциатора. С этой целью:

• на вход подать синусоидальное напряжение с амплитудой 0,5 В,

• изменяя частоту входного сигнала от 100 Гц до 10 кГц снять зависимость U_вых(f) для R_К = 120 Ом, контролируя U_вых вольтметром,

• снять АЧХ для R_К = 300 Ом,

• построить на одном графике зависимости U_вых (f), определить по ним частоты среза (f_ср), письменно объяснить поведение амплитудно-частотных характеристик.

4.4 Снять амплитудно-частотную характеристику дифференциатора в диапазоне частот от 100 Гц до 25 кГц для случая: R_К = 300 Ом, С_К – отсутствует. Построить зависимость U_вых (f), определить по ней частоту среза (f_ср), письменно объяснить поведение АЧХ.

4.5 Исследовать реакцию дифференциатора на подачу прямоугольных импульсов при R_К = 120 Ом, С_К = 0,01 мкФ. Для этого:

• с помощью осциллографа установить следующие параметры прямоугольных импульсов, подаваемых с генератора: амплитуда 2,5 В, частота – 100 Гц,

• подать прямоугольные импульсы на вход дифференциатора,

• зарисовать осциллограммы входного и выходного сигналов на одном графике, измерить с помощью осциллографа и записать их амплитуды,

• повторить эксперимент для частот прямоугольных импульсов 3 кГц, 20 кГц,

• письменно объяснить полученные результаты.

5 СОДЕРЖАНИЕ ОТЧЕТА

1. Наименование и цель работы.

2. Краткие теоретические сведения.

3. Расчетная часть.

4. Экспериментальная часть: схемы, таблицы, графики.

5. Выводы.

6 КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Нарисуйте основные базисные схемы дифференциаторов.

2. Напишите выходные выражения и нарисуйте формы выходных сигналов, если на вход поданы:

а) ступенчатый сигнал;

б) меандр;

в) прямоугольный сигнал;

г) синусоидальный сигнал;

д) косинусоидальный сигнал.

3. Объясните принцип работы дифференциатора.

4. Как влияет величина сопротивления, включенного в обратную связь ОУ.