02_Интеграторы на ОУ

9

Лабораторная работа № 2

ИЗУЧЕНИЕ МЕТОДОВ ПОСТРОЕНИЯ ИНТЕГРАТОРОВ И ИХ ХАРАКТЕРИСТИК

Цель работы: изучение принципа работы и методов построения интеграторов, исследование характеристик интеграторов с помощью лабораторного макета.

1 Краткие теоретические сведения

Широкое применение в аналоговой электронике находят интегрирующие устройства, кроме своего прямого назначения они используются в качестве элементов фильтрации сигналов. Схема простейшего инвертирующего интегратора на ОУ приведена на рис. 2.1.

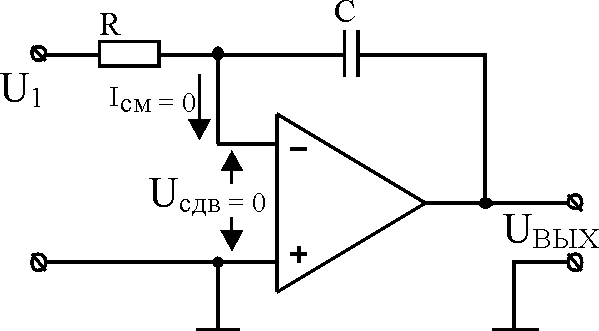
Рис. 2.1 – Схема инвертирующего интегратора на ОУ

Для идеального ОУ для входного тока ί_R и тока через конденсатор ί_C справедливо следующее равенство:

ί_C = – C(dU_вых/dt) = U₁/R = ί_R.

Решая это выражение относительно dU_вых , получим:

dU_вых = − (1/RC)U₁dt.

Интегрируя последнее уравнение, найдем выходное напряжение:

U_вых = .

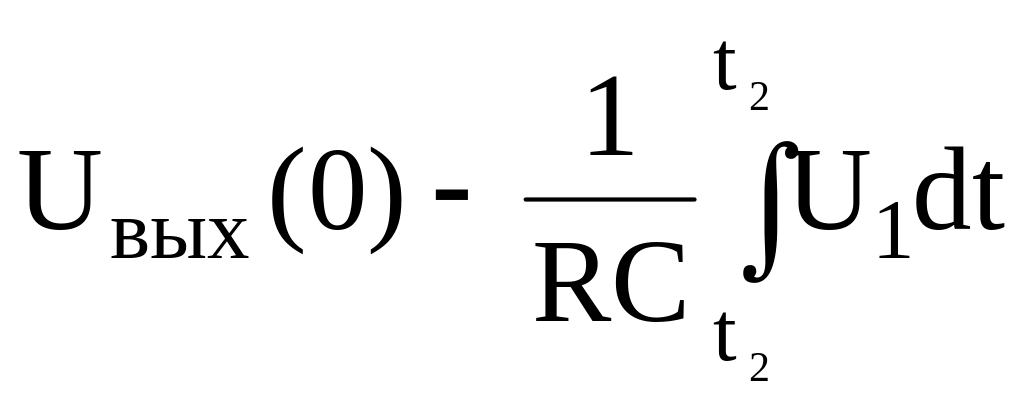Постоянный член U_вых(0) определяет начальное условие интегрирования.

Пределами интегрирования в этой формуле являются моменты времени t₁ и t₂.

В действительности ОУ имеет некоторое напряжение сдвига и нуждается в токе смещения. В интеграторе напряжения сдвига интегрируется как ступенчатая функция, что дает дополнительный линейно нарастающий (или спадающий) выходной сигнал, причем полярность этого сигнала определяется полярностью U_сдв , а наклон – величиной U_сдв.

Ток смещения течет через конденсатор обратной связи C, что также приводит к появлению наклонного выходного сигнала. В результате действия этих двух эффектов конденсатор C через некоторое время зарядится до максимально возможного выходного напряжения усилителя. Такое накопление заряда накладывает ограничение на интервал времени, в течение которого может быть осуществлено интегрирование с достаточной точностью.

Кроме того, напряжение U_сдв добавляется к напряжению на конденсаторе C, и т.к. это напряжение равно U_вых, такая прибавка вносит в результат ошибку, равную U_сдв. В результате выражение для U_вых примет вид:

U_вых = − (1/RC)∙∫ U₁dt + 1/RC)∙∫ U_сдвdt+(1/С)∙∫ I_смdt + U_сдв.

Ошибку напряжения сдвига U_сдв можно уменьшить следующими приемами:

• использовать ОУ с низким U_сдв;

• периодически сбрасывать интегратор (разряжать конденсатор С до некоторого значения);

• шунтировать конденсатор сопротивлением R_p , как показано на рис. 2.2.

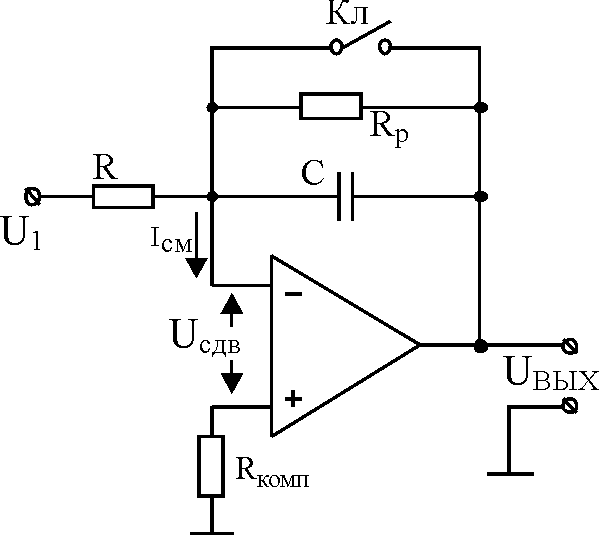
Рис. 2.2 – Схема инвертирующего интегратора на ОУ с шунтирующим резистором в цепи обратной связи

Шунтирование конденсатора C сопротивлением R_p позволяет на низких частотах ограничить напряжение ошибки величиной (R_p/R) U_сдв вместо АU_сдв. Но шунтирование ограничивает снизу область частот, в которой происходит интегрирование.

Слагаемое ошибки в правой части выражения для U_вых, связанное с I_см , можно уменьшить за счет подключения между входом “+” и “землей” компенсационного сопротивления R_комп , равного R  R_p.

Типичные логарифмические амплитудно-частотные характеристики (ЛАЧХ) интеграторов на ОУ с шунтирующим резистором в цепи обратной связи R_p и без него показаны на рис. 2.3.

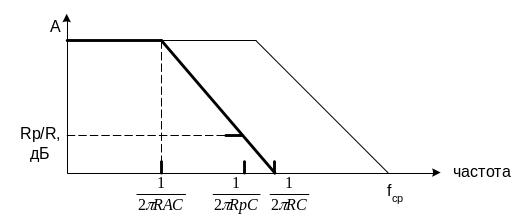
Рис. 2.3 – Логарифмические амплитудно-частотные характеристики интеграторов: тонкая линия – ЛАЧХ ОУ, жирная линия – ЛАЧХ интегратора без R_p, штрихпунктирная линия – ЛАЧХ интегратора при наличии R_p

Для простого интегратора частота среза , где А – коэффициент усиления ОУ. Введение резистора R_p приводит к увеличению частоты среза. Это прямое следствие ослабления эффекта Миллера, связанного со снижением коэффициента усиления на низких частотах от А до величины R_p/R. Частота скорректированного интегратора:

Таким образом, для скорректированного интегратора полоса частот, в которой возможно интегрирование, лежит в области от 1/2πR_pС до 1/2πRС.

2 ПРИМЕРЫ ИНТЕГРИРОВАНИЯ

Пример 1: а) как будет выглядеть сигнал на выходе интегратора, если на его вход подать ступенчатый сигнал (рис. 2.4а),

б) если R = 1 мОм, С = 0,1 мкФ и U_вх = 1 В, то чему равно U_вых через 3 мс после t_o.

Решение:

а) записывая входной ступенчатый сигнал как функцию времени, получим: U_вх = U при t ≥ t_o , U_вх = 0 при t < t_o. Проведем интегрирование, используя первое условие.

U_вых = − (1/RC)∙∫ U_вхdt = − (1/RC)(Ut).

Т.о., изменение U_вых. во времени представляет собой наклонную прямую с полярностью, противоположной полярности U_вх (рис. 2.4б).

а) б)

Рис. 2.4 – Сигнал на входе (а) и сигнал на выходе интегратора (б).

б) вычислим U_вых интегрированием в пределах от t_o = 0 до t₁ = 3 мс.

мВ.

Отметим, что результат интегрирования выражается в виде

и этим выражением можно всегда пользоваться, когда U_вх. – прямоугольный импульс или прямоугольная волна.

Пример 2: а) как будет выглядеть сигнал на выходе интегратора, если на его вход подать импульсы прямоугольной формы (рис. 2.5а).

б) если R = 10 кОм, С = 0,1 мкФ, U_вх=5 В и f = 1 кГц, то чему равна амплитуда выходных импульсов U_вых.

Решение:

а) так как входной сигнал периодический, то для описания выходного напряжения U_вых достаточно рассмотреть один полный период. Запишем U_вх как функцию времени (рис. 2.5а).

U_вх = 5 В при t₁ < t  t₂, U_вх = - 5 В при t₂ < t  t₃

Эту функцию можно интегрировать на каждом из её полупериодов. Для описания выходного сигнала достаточно выяснить его форму и значения U на концах каждого полупериода. Подставив постоянное напряжение в выражение для U_вых, получим:

.

Накопленное напряжение в конце первого полупериода (от t₁ до t₂) равно:

В.

Накопленное напряжение за второй полупериод между t₂ и t₃ равно:

В.

Выходной сигнал показан на рис. 2.5б.

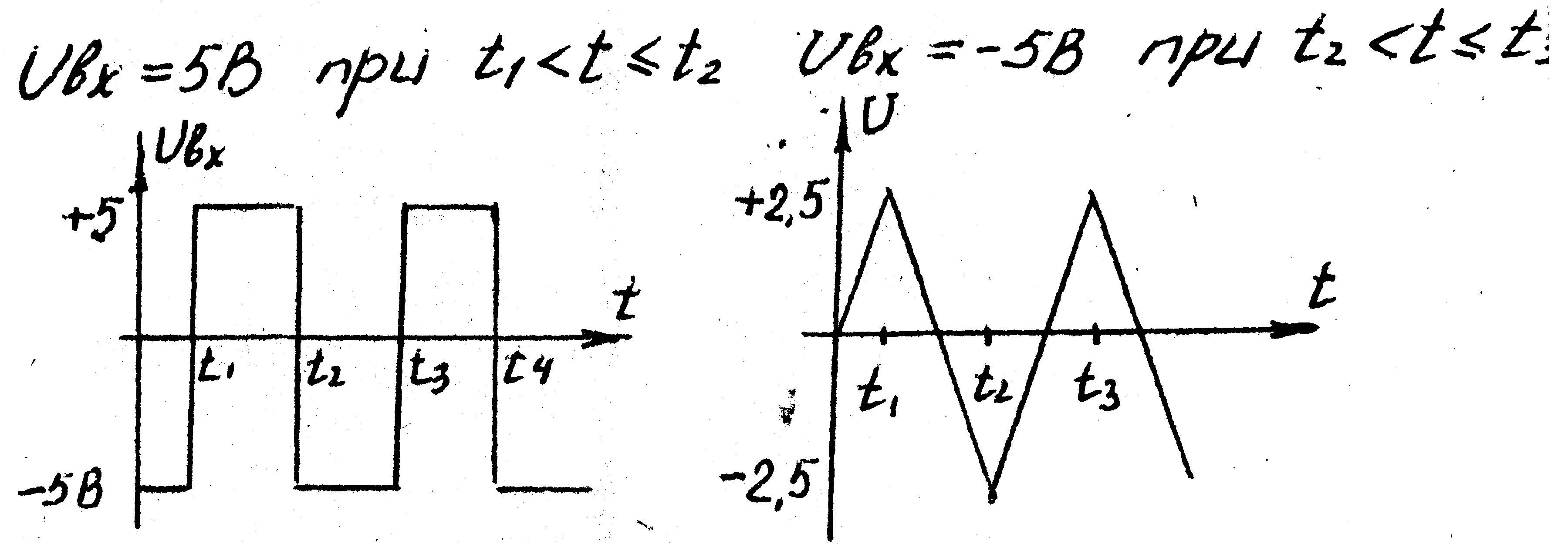
а) б)

Рис. 2.5 – Сигнал на входе (а) и сигнал на выходе интегратора (б).

Пример 3: требуется рассчитать значения R, C, R_p для интегратора с выходной характеристикой с точностью не хуже 2% на частоте f = 20 кГц.

Решение:

а) пусть С = 0,1 мкФ.

Для интегратора выходное напряжение .

Из условия задачи следует равенство: 5000 = - (1/RC), откуда находим кОм.

б) желательная точность интегратора равна 2%. Если f_раб превышает его частоту среза больше чем в 10 раз, то точность интегратора превысит это значение. Поэтому зададим f_ср = 2 кГц.

в) положим R_p/R = 2000. Тогда R_p = 4 МОм → f = 1/2π R_p С < 2 кГц.

Таким образом, R = 2 кОм, R_p = 4 МОм, С = 0,1 мкФ.

3 ПОДГОТОВКА К ПРОВЕДЕНИЮ ИССЛЕДОВАНИЙ

1. Представить преподавателю результаты расчетов и моделирования.

2. Подобрать все необходимые для макетирования компоненты (после окончания работы компоненты возвращаются на место).

3. Собрать схему путем подключения соответствующих компонентов к контактным клеммам макета.

4. Проверить все соединения и после этого показать преподавателю.

ВНИМАНИЕ: включать питание и приборы можно только после проверки схемы преподавателем и получения разрешения!

После того, как монтаж проверен и получено разрешение, можно приступать к исследованиям.

5. Все измерения проводить относительно "земли". Сопротивление нагрузки не должно быть менее 2 кОм, в противном случае ОУ может выйти из строя. Отключать источник входного сигнала до того, как будет выключено питание. В противном случае ОУ может выйти из строя.

4 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

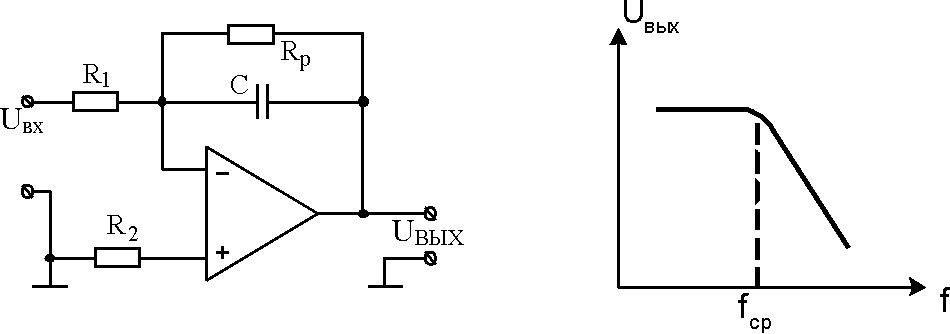
4.1 Собрать схему интегратора, представленную на рис. 4.1а.

а) б)

Рис. 4.1 – Схема интегратора (а) и вид его АЧХ (б)

Выбрать следующие номиналы компонентов:

R₁ = 10 кОм,

С = 0,01 мкФ,

R_p = 51 кОм, 82 кОм, 100 кОм,

R₂ = 10 кОм.

4.2 Включить осциллограф С8-39 и комплекс КУЛ-1. Подать напряжение питания на лабораторный макет от КУЛ-1 (использовать выходы +12В и -12В).

4.3 Снять амплитудно-частотные характеристики интегратора К, дБ (f). Для этого:

• на вход подать синусоидальное напряжение с амплитудой 0,5 В,

• изменяя частоту входного сигнала от 100 Гц до 50 кГц, снять зависимость U_вых(f) для R_p = 51 кОм, контролируя U_вх и U_вых вольтметром,

• для каждого значения частоты вычислить К и К, дБ,

• результаты измерений свести в таблицу.

Таблица 4.1 – Результаты измерений

f
Uвх
Uвых
К
К, дБ

• снять АЧХ для R_p = 82 кОм и R_p = 100 кОм в том же диапазоне частот,

• построить на одном графике зависимости К, дБ (f), определить по ним частоты среза (f_ср), письменно объяснить поведение амплитудно-частотных характеристик.

4.4 Исследовать реакцию интегратора на подачу прямоугольных импульсов. Для этого:

• с помощью осциллографа установить следующие параметры прямоугольных импульсов, подаваемых с генератора: амплитуда 5 В, частота – 1 кГц,

• подать прямоугольные импульсы на вход интегратора,

• зарисовать осциллограммы входного и выходного сигналов на одном графике, измерить с помощью осциллографа и записать их амплитуды,

• повторить эксперимент для частот прямоугольных импульсов 100 Гц, 10 кГц,

• письменно объяснить полученные результаты.

5 СОДЕРЖАНИЕ ОТЧЕТА

1. Наименование и цель работы.

2. Краткие теоретические сведения.

3. Расчетная часть.

4. Экспериментальная часть: схемы, таблицы, графики.

5. Выводы.

6 КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Объяснить принцип работы интегратора.

2. Нарисовать принципиальную схему интегратора и объяснить назначение компонентов.

3. Нарисовать форму выходного сигнала и написать её алгебраическое выражение, если на вход поданы следующие сигналы:

а) прямоугольный сигнал;

б) треугольный сигнал;

в) синусоидальный сигнал;

г) косинусоидальный сигнал.