§ 55. Кинетический момент механической системы относительно центра и оси

Кинетическим моментом или главным моментом количеств движения механической системы относительно данного центра называют вектор, равный геометрической сумме моментов количеств движения всех материальных точек системы относительно этого центра.

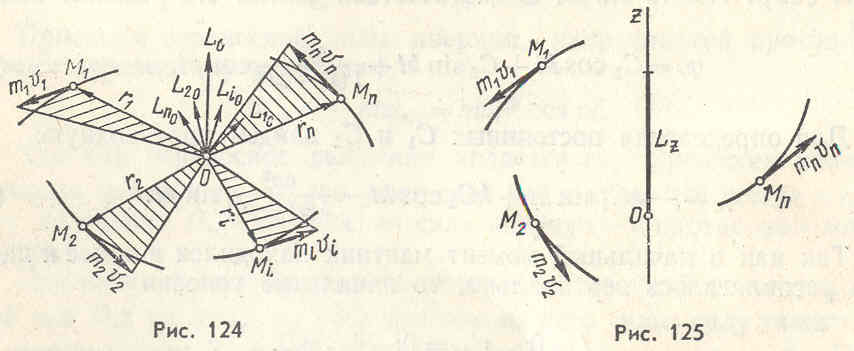
Момент количества движения каждой материальной точки системы (рис. 124) относительно центра О определяется по формуле (53.2)

Кинетический момент механической системы относительно центра О: (55.1)

Кинетическим моментом, или главным моментом количеств движения механической системы относительно оси, называется алгебраическая сумма моментов количеств движения всех материальных точек системы относительно этой оси.

Момент количества движения каждой точки системы (рис. 119, б) относительно оси Oz определяется согласно (53.3).

Кинетический момент системы относительно оси (рис.125) (55.2)

Кинетические моменты механической системы относительно некоторого центра О и какой-либо оси Z, проходящей через этот центр, связаны такой же зависимостью, как и главные моменты системы сил относительно центра и оси, т. е.

(55.3)

Таким образом, проекция кинетического момента механической системы относительно некоторого центра О на ось, проходящую через этот центр, равна кинетическому моменту системы относительно этой оси.

§ 56. Теорема об изменении кинетического момента механической системы

Положим, что система материальных точек M₁ М₂,…,М_п движется под действием некоторой системы сил, которые разделим на внешние силы и внутренние силы . Выберем некоторый неподвижный центр О и определим изменение момента количества движения каждой точки М_k относительно этого центра по уравнению (54.2): (k=1,2,…,n)

Просуммируем полученные n уравнений: (a)

Как указывалось в § 31, геометрическая сумма моментов всех внутренних сил относительно любого центра равна нулю, т. е. . Преобразуем левую часть равенства (а), учитывая (55.1):

Тогда уравнение (а) принимает вид (56.1)

Уравнение (56.1) выражает теорему об изменении кинетического момента механической системы: производная по времени от кинетического момента механической системы относительно некоторого неподвижного центра геометрически равна главному моменту внешних сил, действующих на эту систему относительно того же центра.

Векторному равенству (56.1) соответствуют три равенства в проекциях на оси координат: , , (56.2)

Здесь согласно (55.3) L_x, L_y, L_z - кинетические моменты механической системы относительно осей координат, a - главные моменты внешних сил относительно этих осей.

Уравнения (56.2) показывают, что производная по времени от кинетического момента механической системы относительно некоторой оси равна главному моменту внешних сил относительно этой оси.

Следствия из теоремы. 1. Если главный момент внешних сил относительно некоторого неподвижного центра остается все время равным, нулю, то кинетический момент механической системы относительно этого центра остается постоянным.

Из уравнения (56.1) следует, что если , то

и (56.3)

2. Если главный момент внешних сил относительно некоторой оси остается все время равным нулю, то кинетический момент механической системы относительно этой оси остается постоянным.

Из уравнений (56.2) следует, что если, например, , то

и (56.4)

Следствия из теоремы об изменении кинетического момента механической системы выражают закон сохранения кинетического момента механической системы.