2.2 Напряженное состояние

В зависимости от способа приложения внешних сил к телу в нем возникают различные напряженные состояния.

При действии одного главного напряжения σ₁, когда σ_{2 =} σ₃ = 0, возникает одноосное напряженное состояние, Такое состояние наблюдается, например, при растяжении на разрывной машине гладкого разрывного образца. При испытании тонкостенных цилиндрических емкостей под внутренним давлением действуют два главных напряжения при σ₃ =0. В этом случае возникает двухосное напряженное состояние. Комбинируя знаки и величины напряжений, можно получить различные схемы двухосного нагружения (рис.2.2), резко различные по воздействию на тело.

Рис.2.2. Схемы двухосного нагружения

Трехосное напряженное состояние (его часто называют объемным) достигается при одновременном действии трех главных напряжений, σ₁, σ₂, σ_3. Такую ситуацию можно создать, например, при помещении твердого тела в жидкость, находящуюся под давлением (гидростатическое сжатие). Тогда σ_{1 =} σ_{2 =} σ₃ < 0.

2.3 Деформация и деформированное состояние

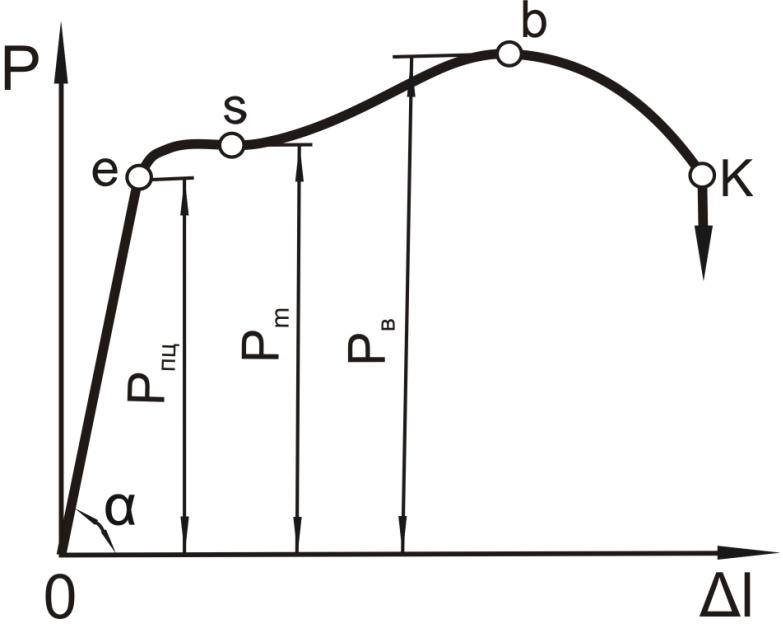
Под действием внешних сил твердое тело деформируется, изменяет свою форму и размеры. Рассмотрим испытание металлического образца растяжением на разрывной машине. В процессе испытания записывается диаграмма деформации (рис.2.3) - изменение длины образца Δl от величины растягивающего усилия (P). Диаграммой фиксируется ряд предельных состояний испытуемого материала.

Дадим слегка упрощенное описание диаграммы. В начальной стадии испытания от 0 до е машина записывает прямолинейный участок, на котором приращение силы пропорционально приращению удлинения, что свидетельствует о выполнении закона Гука. В своей простейшей форме этот закон выражается следующей формулой:

σ = Е·e, (2.2)

где σ - нормальное напряжение; е= Δl /l₀ - относительное упругое удлинение; Δl – абсолютная упругая деформация; l₀ - рабочая длина образца; Е – коэффициент пропорциональности (постоянная данного материала или его модуль упругости). Точка е на диаграмме ограничивает максимальную си-

	лу, до которой сохраняется действие закона Гука. При нагружении до точки е после снятия нагрузки образец полностью возвращается к первоначальным размерам и не получает остаточной деформации. Иначе говоря, в этой области нагружения образец деформируется упруго и деформации, как абсолютная (Δl), так и относи-
Рис.2.3. Диаграмма растяжения

тельная (е) являются упругими и обратимыми. Дальнейшее нагружение образца выше точки е приводит к пластической деформации материала, которая остается после снятия нагрузки, т.е. происходит остаточное формоизменение тела. Расчет относительной пластической деформации производится аналогично упругой деформации.

Закон Гука справедлив и для касательных напряжений в форме

τ = G·g, (2.3)

где G -модуль упругости при сдвиге (модуль сдвига); g - относительный сдвиг.

Между модулями упругости G и Е существует связь

G = Е/2(1 + μ), (2.4)

где μ - коэффициент Пуассона, или коэффициент поперечной упругой деформации. Его теоретическое значение для упругого твердого тела равно 0,25, а, фактически, на упругодеформированных металлах он достигает 0,3 - 0,32.

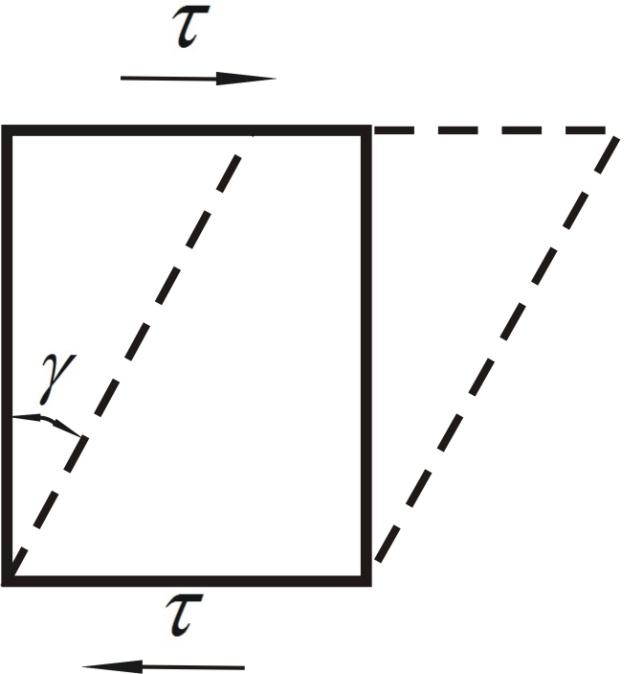
	Рассмотрим определение величины сдвига. Выделим элементарный объем, на который действует касательное напряжение τ (рис.2.4). В результате произойдет сдвиг на угол γ. Относительный сдвиг при этом определится по формуле g = tg γ. По аналогии с напряжениями можно представить себе, что в общем случае в твердом теле
Рис. 2.4. Сдвиг элементарного обьема

будет существовать система относительных деформаций, или тензор деформаций: е_x, e_y, e_z; g_ху, g_xz, g_yz.

Подобно максимальным касательным напряжениям существуют и максимальные сдвиги. Максимальный сдвиг, который претерпело твердое тело, можно рассчитать по формуле g_max = e_max – e_min, где e_max и e_min - наибольшее (с учетом знака) и наименьшее главные удлинения.

Сведения о напряжениях и деформациях, приведенные выше, необходимы для понимания роли дефектов кристаллической решетки для прочности металлов. Например, некоторые металлы становятся хрупкими и ненадежными в работе, если детали, сделанные из них, работают в условиях объемнорастягивающего напряженного состояния. Эти же металлы были вполне прочными и надежными, когда работали при одноосном растяжении. Известно также, что пластичность металла осуществляется главным образом сдвигами по плоскостям кристалла, где наиболее велики напряжения сдвига. Роль нормальных напряжений, очевидно, является главной при разрушении металла, разрыве связей между атомами.