7.3 Формирование геометрически необходимых дислокаций при наклепе

При нагружении выше предела текучести в полукристаллических металлах и металлических сплавах упругая деформация сменяется пластической. Однако, даже в чистых поликристаллах, не говоря о сплавах, обычно состоящих из смеси кристаллов основного, часто мягкого металла и кристаллов другого вещества, более твердых, чем основа, вступление в пластическое состояние не происходит одновременно во всех кристаллах образца. Деформация между ними распределяется неоднородно (негомогенно).

Физической причиной негомогенной деформации для поликристаллов является анизотропия их механической прочности, то есть её зависимость от направления кристаллографических осей. Если деформацию осуществлять в каком-либо определенном направлении, то в одних кристаллах пластическое течение начинается легче и раньше и происходит полнее, чем в других. Еще резче выражено явление в смеси мягких и твердых кристаллов, составляющих металлический сплав, твердые частицы часто вообще не деформируются.

Чем больше развита негомогенность (неоднородность) распределения деформации, тем больше такой металл склонен к хрупкости и менее надежен в работе тяжело нагруженной конструкции.

В работах Эшби дана попытка создания дислокационной теории негомогенной пластической деформации кристаллических тел. Эшби принял, что при пластической деформации кристаллических сплавов плотность дислокации ρ, участвующих в деформации, состоит из двух, независимо развивающихся частей: , где - плотность обычных дислокаций, необходимых для изменения формы тела пластической деформацией. Эшби назвал их статическими дислокациями; - плотность дополнительных дислокаций, вызванных неоднородностью (негомогенностью) пластической деформации. Эшби назвал их геометрически необходимыми, т.к. их появление связано с необходимостью согласования деформации соседних кристаллов или разнородных частиц сплава. Альтернативой этой совместимости деформации является только образование пор, микротрещин и других несплошностей. Либо деформация соседних частиц или кристаллов будет согласована и тогда неизбежно появятся геометрически необходимые дислокации, либо будут образовываться микроочаги разрушения. Именно этим и объясняется большая склонность неоднородных металлов к хрупкому разрушению.

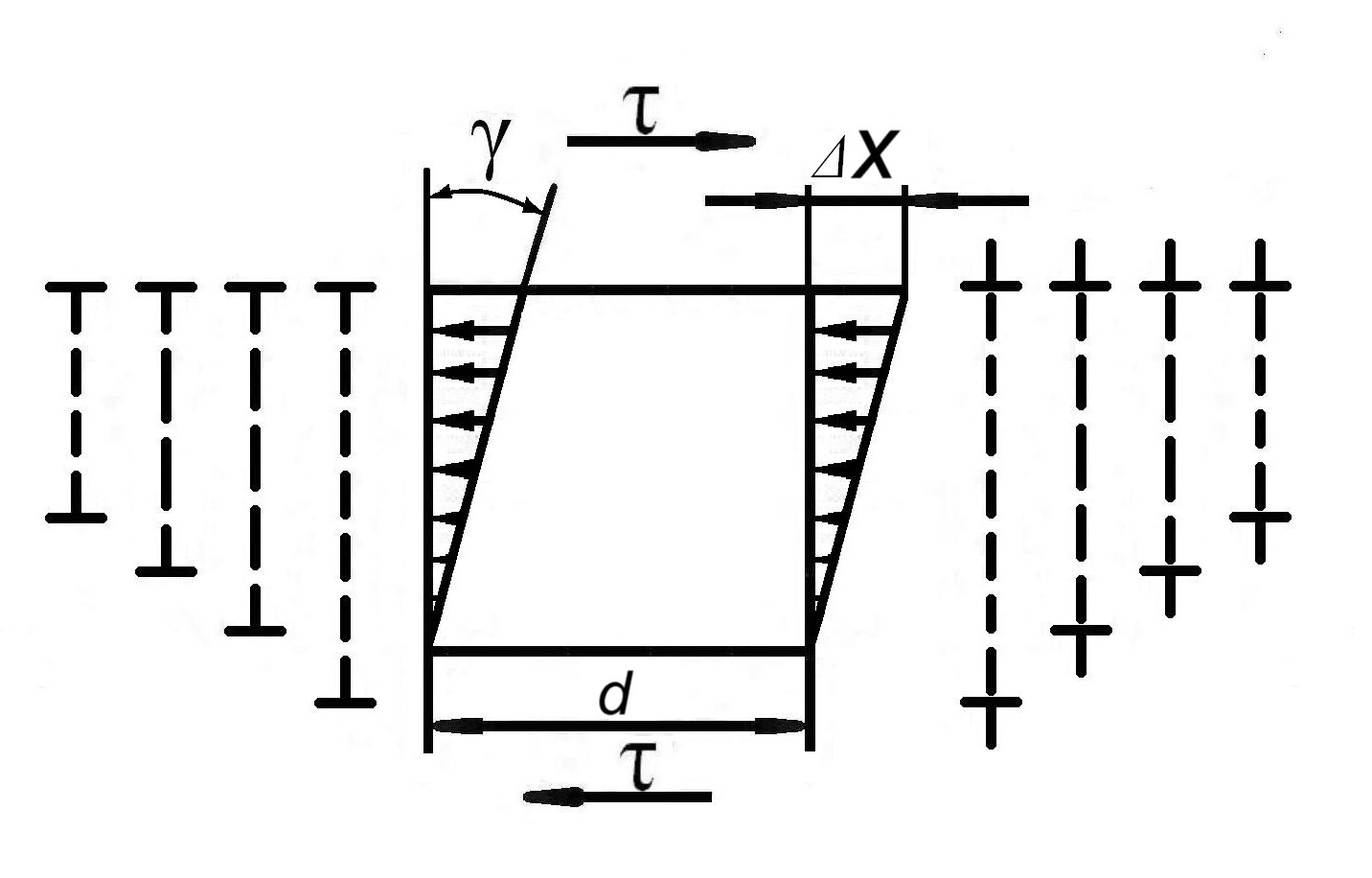
Рассмотрим пример расчета для сплава, в котором мягкий металл содержит равномерно распределенные твердые (недеформирующиеся под нагрузкой) частицы. Их форму примем для простоты кубической с размером грани d (рис. 7.4).

Рис. 7.4. Модель деформирования матрицы с твердой частицей	Рис. 7.5. Модель формирования призматических дислокационных петель

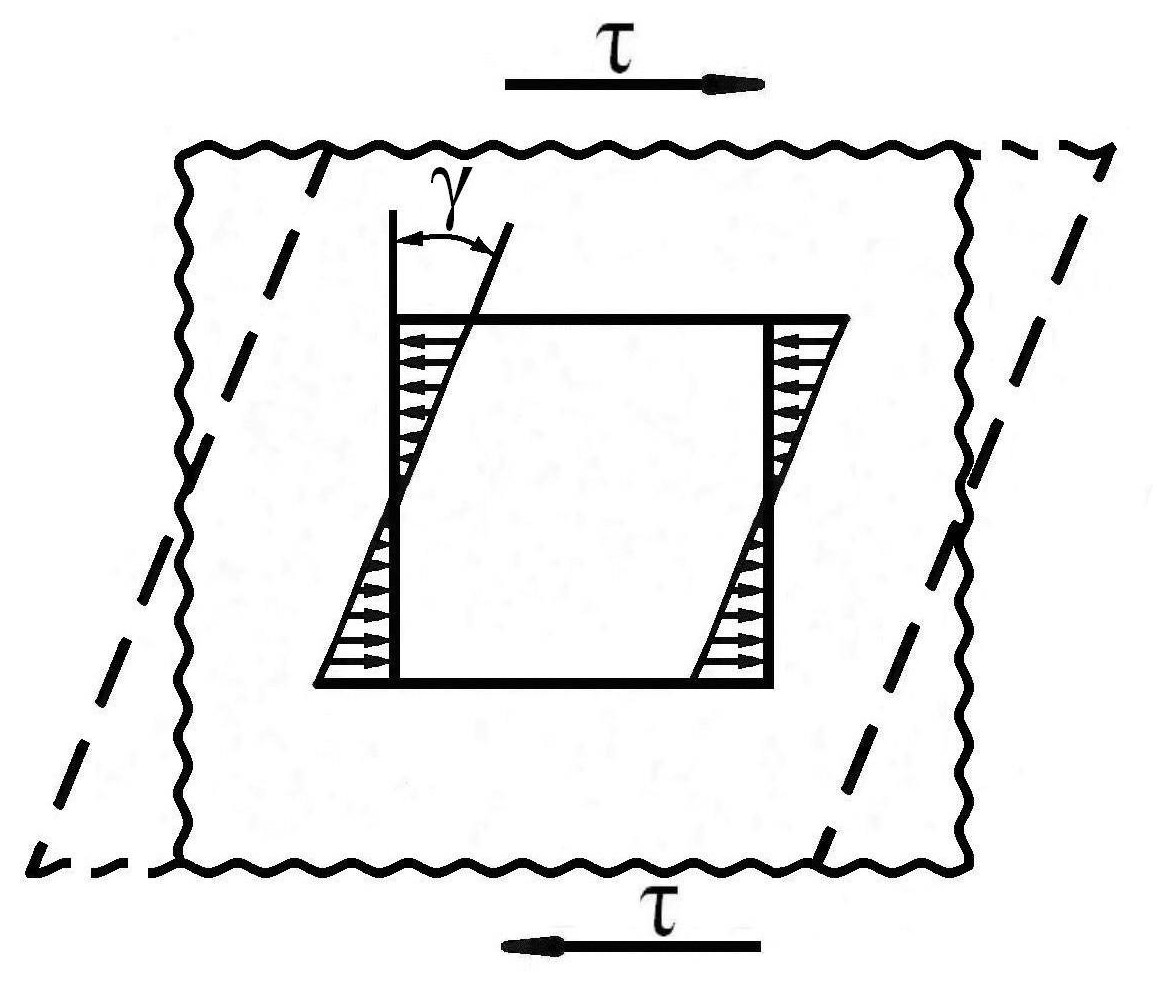
Если к металлу приложено напряжение τ, большее, чем предел текучести металла, то объем мягкого металла, окружающий твердую частицу, претерпит пластический сдвиг на угол γ (относительная сдвиговая деформация будет равна ). Так же должна была бы деформироваться и твердая кубическая частица (показано пунктиром).

Однако, по условию модели, частица неспособна пластически деформироваться и не разрушается. Тогда в мягком окружающем частицу металле (матрице) появятся пластические возмущения, аналогичные тому, как если бы мы вернули условно сдвинутую на угол γ твердую частицу обратно в её исходное несдвинутое состояние (показано на схеме рис. 7.4 стрелками).

Такое обратное мысленное возвращение частицы к исходной форме не может произойти без пластической деформации прилегающего к частице мягкого металла. Эшби проанализировал способы, какими такой процесс может осуществиться.

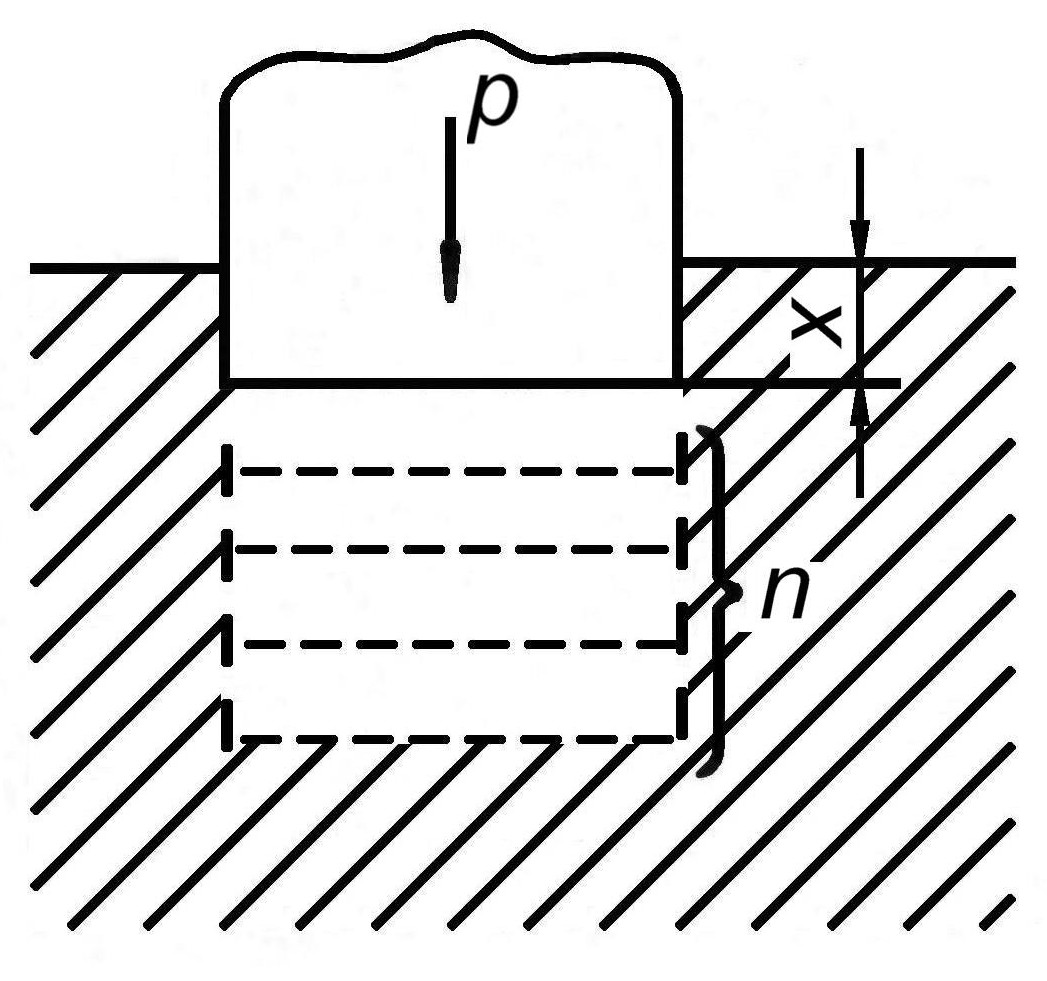
Представим себе, что твердый цилиндр-пуансон вдавливается силой Р в поверхностные слои полупространства из мягкого металла (рис.7.5). Когда пуансон вдавится на величину х, то под пуансоном появятся дислокационные петли, по форме близкие к окружности пуансона, которые получили название призматических. Число этих петель может быть рассчитано по выражению: n = x/b, где b - вектор Бюргерcа. Очевидно, призматические петли появятся только при условии, когда сила Р вызывает пластическое, а не упругое, вдавливание цилиндра в мягкий металл.

На схеме рис. 7.6 показано, как возле твердой кубической частицы, соответствующей рис. 6.4, появляются призматические петли. Их число возле одной частицы будет равно . Если f - объемная доля твердых частиц в сплаве, то количество петель N в единице объема можно получить, умножив n на число частиц в нем, равное . Длина дислокаций в одной петле ~ 4d. Тогда плотность геометрически необходимых дислокаций ρ_г.н будет равна:

. (7.1)

Рис. 7.6. Формирование призматических дислокационных петель возле твердой кубической частицы

Эшби дал общее выражение для плотности геометрически необходимых дислокаций, введя обобщенный структурный параметр η: . (7.2) Для сплавов, содержащих приблизительно равноосные твердые частицы -

включения, (d - средний размер частицы, f - их объемная доля в сплаве). В сплавах, содержащих твердые частицы в виде пластинок, в которых один размер много меньше двух других, η равно среднему расстоянию между твердыми пластинками. В чистых поликристаллах η пропорционально среднему размеру зерен - кристалликов. Как видно, в любом примере сплава количество геометрически необходимых дислокаций полностью определяется размером характерного элемента его микроструктуры. Чем больше число таких дислокаций, тем в большей мере именно они, их появление, будут определять свойства металла, его поведение под нагрузкой.

Так, например, во многих исследованиях установлено прямыми наблюдениями, что почему-то чаще всего генераторы дислокаций (источники Франка-Рида) расположены возле границ между зернами. Очевидно, необходимость появления геометрически необходимых дислокаций объясняет это. Давно уже известно металловедам явление так называемого фазового наклепа. Если металлический сплав состоит из твердого раствора двух разных металлов, то в определенных условиях иногда возможна и в ряде случаев очень интересна для благоприятного изменения свойств сплава химическая реакция между атомами двух металлов, составляющих сплав. В итоге внутри сплава образуются сначала отдельные молекулы, а затем мелкие частицы интерметаллидов, более или менее равномерно распределенные в объеме сплава. Как правило, эти интерметаллидные частицы значительно тверже, чем металлы, из которых они получились, а плотность их меньше плотности сплава. Поэтому образующаяся частица интерметаллидного химического соединения должна при своем росте как бы расталкивать, отодвигать окружающий её металл, то есть пластически деформировать его. Это явление и называется фазовым наклепом. Аналогичная ситуация обычно возникает и при полиморфных превращениях. Например, альфа-железо, имеющее ОЦК - решетку, обладает меньшей плотностью, чем гамма-железо (ГЦК - решетка). Полиморфное превращение гамма-альфа в железе, идущее при охлаждении железа от высоких температур (особенно при ускоренном охлаждении), так же должно сопровождаться фазовым наклепом.